Étiquette : Paul le poulpe

Effet Pangloss : les dangers des raisonnements à rebours

Aujourd’hui je vous propose de regarder de près un raisonnement qui a l’air tout à fait anodin mais qui peut se révéler terrifiant. Ce raisonnement consiste à penser à rebours. À la manière de ces poils qui poussent à l’envers et s’enkystent dans la peau, il est agaçant et difficile à éliminer, quelle que soit la dose de crème dont on l’enduit. Il est bien plus répandu qu’on ne le pense, et nous allons essayer de le débusquer au travers de quelques exemples.

Le Loto

Je vais partir de la loterie nationale française, ledit Loto. Ayant pour objectif de nous soutirer jusqu’à nos derniers sous en nous faisant miroiter une lointaine et peu probable carotte, ce jeu, nous allons le voir, ressemble à une forme élaborée de soumission librement consentie. Si nous avons un élève de terminale scientifique à portée de main, demandons-lui d’évaluer nos chances de nous faire détrousser, c’est à son programme de maths. Sinon, nous allons le faire ensemble, ce n’est pas très compliqué.

« Le loto, c’est facile, c’est pas cher, et ça peut rapporter gros ». Slogan de 1984.

Depuis 2008, le nouveau Loto (qui est plus difficile à remporter que l’ancien si l’on compare) demande d’obtenir 5 numéros parmi 49, ainsi que le numéro « chance » tiré parmi 10. Le nombre de tirages possibles se calcule ainsi :

Sachant qu’il y a trois tirages par semaine (le lundi, le mercredi et le samedi), une personne dotée d’une espérance de vie à la naissance de 2010 en France (moyenne Femmes-Hommes : environ 82 ans) et qui, chose invraisemblable, jouerait dès le berceau à tous les tirages aura rempli le jour de sa mort 82 (ans) x 52 (semaines) x 3 (tirages) soit quelque chose comme 13000 grilles, en voyant large. Ça lui donne un peu moins d’une chance sur mille de gagner une fois la cagnotte. C’est peu.

Pour avoir un autre ordre d’idée, nous pouvons prendre le taux annuel moyen de mortalité d’un individu garçon de 33 ans vivant en France comme moi, qui est de 119 sur 100 000 (soit 1 sur 840) – qui signifie qu’un type en France a une chance sur 840 de mourir dans l’année de ses 34 ans. Partons du principe que la probabilité de mourir est uniforme tout le long de l’année. Lorsque j’achète un billet de loto j’ai autant de « chances » de mourir dans les 24 minutes qui suivent que de gagner le gros lot. Si j’avais 90 ans, j’aurais autant de chance de gagner le gros lot que de ne pas survivre 9 secondes à l’achat du billet¹.

En clair, un individu guidé par sa seule raison refuserait de claquer ses étrennes comme ça. Mais l’humain n’est pas toujours rationnel, loin de là. Et à l’orée du bois, les tire-laine guettent.

Monique Pinçon-Charlot et Michel Pinçon, deux sociologues ont décrypté le comportement des vainqueurs du Loto dans Les millionnaires de la chance (Payot, Paris, 2010). Ils expliquent que certains individus jouent au Loto en sachant bien que les chances de gagner sont minces, mais… moins minces que celles de changer de classe sociale. En d’autre terme, il serait plus probable pour les classes pauvres de devenir riche en cochant les cases qu’en travaillant d’arrache-pied – ce qui fait réflechir sur le  « mérite » et les encouragements à travailler plus.

Où est le raisonnement à rebours ? Il arrive.

Et les 100% de perdants ?

L’argument massue qui a été employé pour nous faire jouer pendant des années était, rappelons-nous : « 100% des gagnants auront tenté leur chance ».

Ce slogan, à bien y regarder, ne veut pas dire autre chose que ceci : « tous ceux qui ont gagné ont joué », ce qui ne nous apprend rien : on ne gagne pas au loto, au football ou au poker à l’insu de son plein gré – quoi que, lors des matchs nationaux de football, on en voie certains hurler en ville « on a ga-gné » alors qu’ils n’ont pas joué, que voulez-vous, c’est le charme chauvin du sport.

Le séduisant de l’affaire est qu’on nous édicte une règle sur les gagnants. Et comme vous et moi voudrions tous gagner, on se dit tiens, comment ont-ils fait ? Ont-il trituré un trèfle, un fer à cheval ? Eh bien non, ils se sont contenté de jouer. Ils ont tenté leur chance. Voilà. Mais si on y pense, la même chose est valable pour les perdants. Car, c’est ce que la Française des jeux ne nous dit pas : « 100% des perdants ont eu aussi tenté leur chance ! ». Et comble des choses, le 100% des perdants est vachement plus nombreux que le 100% des gagnants. Il n’y a pas beaucoup de gagnants, alors qu’il y a plein de perdants. Mathématiquement, ça se calcule, on a une chance de gagner le gros lot sur 19 millions et quelques (voir le tout premier calcul).

Chercher des raisons

Examinons maintenant ce qui se passe dans la tête d’un joueur lambda.

Quand il perd, il a une forte tendance à se dire quelque chose comme « la chance n’était pas là », puis à shooter dans une boîte de conserve qui traîne. C’était la normalité, qu’il ne gagne pas, il n’était pas dupe, il conclut parfois d’un l’air las « je ne gagne jamais, de toute façon » ou « de toutes les manières je n’ai jamais eu de chance au jeu ». Mais là où le perdant a somme toute un côté assez pragmatique, le gagnant lui, pas du tout ! Il en est même agaçant : il commence déjà par être content de lui, ce qui est une réelle faute de goût. Puis il se trouve plein de bonnes « raisons », comme « je le méritais », ou alors « j’ai joué les bons numéros », « je le sentais », etc.

C’est là que commence le raisonnement à rebours.

Les psychologues sociaux mettent des mots à cela, et c’est bien pratique : le perdant aura un « locus de contrôle » externe (la cause de son échec est le manque de chance, extérieur à lui), tandis que le gagnant aura un « locus de contrôle » interne (il attribue sa réussite à ses qualités propres, ce qui est horripilant). Depuis les travaux de Miller & Ross en 1975, on parle de biais d’autocomplaisance.

Rebours, rebours et ratatam

À chercher une raison pour avoir gagné, la tendance est forte à aller la trouver dans son mérite personnel, comme si le Hasard personnalisé se souciait d’évaluer nos mérites respectifs. Ou dans un coup du sort, comme une espèce d’ange gardien qui veille sur nous. Cela rejoint, vous vous rappelez peut être, le biais du monde juste (cf. Traverse N°1).

C’est effectivement le hasard (sans H majuscule) qui fait la différence entre le gagnant et le perdant. Si les 19 millions et quelques combinaisons possibles sont jouées, la probabilité que quelqu’un gagne est de 1 (on dit 1, mais ça veut dire 100%, tout comme une proba de 0,5 veut dire 50%).

Qu’il y ait un gagnant dans ces cas-là n’est pas une surprise. C’était même quasi-certain. L’incertain, c’est sur qui ça va tomber. Que ça tombe sur moi ou un inconnu, au fond, ce n’est qu’un aléa : il n’y a logiquement aucune conclusion à tirer, ni sur la beauté du monde, ni sur les numéros joués. Pourtant, c’est trop dur : devant la rareté statistique, on cherche une raison à rebours. Alors on se dit au choix

On se dit que quelque part (où ?) quelque chose (immatériel ?) comme la Chance lui a souri (avec quelles dents ?).

Mais le hasard n’est pas gentil. Ni méchant. En tant que volonté, il n’ « est » pas. Il n’obéit à rien, il se contrefout royalement de vous et de moi. Il ne se « contrefout » même pas.

Le sentiment d’avoir déjoué la volonté du Destin est d’ailleurs telle que bien peu veulent rejouer la semaine suivante la combinaison qui a déjà gagné, comme si elle était usée – ce qui n’a pas de sens, les tirages étant indépendants les uns des autres (on appelle ça le sophisme du joueur, je le dis pour l’anecdote).

Raisonnement à rebours sur la bière, selon frère Joseph (extrait de Jean Van Hamme, Francis Vallès, Les maîtres de l’orge, vol. 1 1854, Charles).

Un balcon sur la tête de Tante Olga

Ce raisonnement à rebours nous arrive aussi en cas de coup dur. On a tous une histoire tragique en stock, comme un balcon qui se décroche juste au dessus de la tête d’une Tante Olga. Alors que la « normalité » est de ne pas se prendre le balcon sur la face (tout comme perdre au Loto), là, on se dit qu’il a « manqué » quelque chose à Tante Olga, du pot, de la veine, de la baraka, du cul bordé de nouilles. On se hasarde même à penser que les desseins du Seigneur sont impénétrables, ou que rien n’arrive par hasard, ou que c’était son karma, et qu’elle paye des vies antérieures plutôt fautives. Il se trouvera bien un vieux voisin un peu aigri, une vieille voisine grincheuse pour dire qu’au fond, entre nous, elle ne l’a pas volé². Mais l’erreur est toujours la même : on se retrouve à raisonner à rebours sur ce cas seulement, et on oublie de replacer le cas dans la statistique de toutes les tantes (ou oncles) du monde qui se sont promenées un jour en passant sous un balcon et à qui il n’est rien arrivé, surtout pas un balcon.

Le TSD (tri sélectif des données)

Allons plus loin. Imaginons qu’à la terrasse d’une taverne, seul-e comme un menhir, vous jouez à pile ou face. Quelle est la probabilité d’obtenir cinq fois pile d’affilée ? Facile. 1 chance sur 2 au premier lancer (soit 0,5), pareil pour le deuxième, etc. Ça donne : 0,5×0,5×0,5×0,5×0,5 = 0,0312 environ, ça veut dire environ 3 chances sur 100.

Imaginons maintenant que dans 64 autres tavernes, 64 autres comme vous s’emmerdent à mourir et fassent la même chose. Là, la probabilité que vous fassiez 5 fois pile est toujours la même, mais la probabilité que l’un d’entre vous fasse 5 fois pile est, quant à elle, immense : il est quasiment certain que l’un des joueurs fera ce résultat. Et s’il est tout seul et ne regarde que sa lorgnette, il va conclure qu’il est quand même sacrément doué.

On a envie de sourire, tellement c’est simple, et pourtant, cette erreur qui consiste à extraire le résultat extraordinaire de sa souche statistique et de le brandir comme un étendard est à la base de tout un tas de « miracles ». En voici quelques-uns.

Ötzi la momie

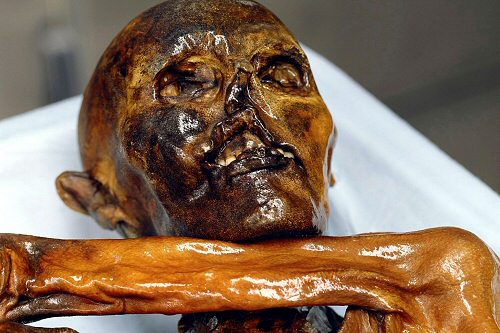
Prenons la malédiction de la momie Ötzi : ce chasseur vieux de cinq milles ans retrouvé congelé en 1991 dans les alpes italo-autrichiennes aurait causé la mort de six personnages l’ayant approché de près, trois scientifiques, un journaliste, un guide de haute montagne, etc. Sachant le nombre conséquent de gens qui ont gravité autour du corps, depuis les expertises lors de sa découverte jusqu’aux visiteurs du musée italien de Bozen-Bolzano où il réside désormais, est-il si extraordinaire que six d’entre elles meurent, surtout lorsqu’elles sont soit pas spécialement jeunes (cinq sur six avaient plus de 50 ans) soit une profession à risque (guide de haute montagne, tué par une avalanche) ? Si l’on compare le nombre de morts rapporté au nombre de personnes qui ont approché Ötzi et sont restées vivantes, l’hypothèse de la malédiction, tout comme les dents de la momie, se déchausse.

Paul le poulpe

Il était une fois une pieuvre qui, durant la coupe d’Europe 2008 et la coupe du Monde 2010 de football masculin, a su déterminer douze des quatorze résultats d’épreuve qui lui ont été demandés. Certaines mauvaises langues disent que la pieuvre aurait actuellement moins d’un an (fin 2010), ce qui implique soit que le poulpe remonte le temps, soit qu’il y a eu deux poulpes, mais enfin peu importe.

 

Ce poulpe mâle, appelé Paul a mérité son surnom d’oracle d’Oberhausen en choisissant, soit disant avec une chance sur deux l’une des deux boîtes affublées des couleurs de chaque équipe (voir l’illustration) En évaluant ce que représentent 12 bonnes réponses sur 14, et en partant du principe qu’il ne pronostique pas les matchs nuls, la probabilité de réussite du poulpe par hasard était de 0,56 %, en gros une chance sur 200. A priori balèze, donc, l’octopode ! Mais bien peu ont enquêté sur le nombre de céphalopodes, de poissons, oiseaux ou autres bestioles de part le monde à qui on s’amuse à poser la question. Si un allemand sur 400 000 fait le coup avec un animal quelconque, on est assuré d’avoir au moins un labrador, un iguane ou un canard cendré qui aura un tel résultat par pur hasard. Suffit de placer ensuite le projecteur des médias sur l’œil humide du vainqueur, en évinçant tous ceux qui ont échoué, et le scénario de l’animal extraordinaire au tentacule malicieux peut se dérouler dans notre vitreux petit écran.

Est-ce risqué d’aller à Lourdes ?

C’est sensiblement le même processus pour les miracles de guérison de Lourdes. On ne peut que s’extasier des 67 miracles revendiqués par l’Église catholique sur le lieu saint depuis les visions de Bernadette Soubirous en 1858, mais posons-nous la question : y-a-t-il réellement plus de guérisons extraordinaires là-bas qu’ailleurs ?

Comme les chiffres sont assez imprécis, nous allons faire une simple estimation.

La principale étude de guérisons considérées comme miraculeuses en milieu hospitalier, là où on trouve un grand nombre de malades, a été réalisée dans le titanesque travail d’archives de O’Regan et Hirshberg³. Leurs résultats sur 128 ans indiquent que, le « taux de miracle » en hôpital est d’environ un cas sur 100 000. Comme la Commission médicale internationale de Lourdes ne prend pas en compte les 70 % de rémissions liées au cancer (car elles sont généralement précédées d’une thérapie, ce qui dilue la part du miracle), il nous reste quelque chose comme un cas de rémission pour 333 000 personnes dans les hôpitaux. Autrement dit, il y a dans les hôpitaux un cas « comme à Lourdes » sur 333 000.

Puisqu’une bonne partie des miracles eut lieu avant de véritables expertises scientifiques, et sont peu fiables même de l’avis de médecins de la Commission d’expertise, nous allons raisonner sur les cinquante dernières années, lors desquelles 5 miracles eurent lieu. Pour se donner une idée, pensons que le dernier en date, reconnu en 2005, porte sur une dame appelée Anna Santaniello, miraculeusement guérie en … 1952. Gardons tout de même ces 5 derniers cas.

Le secrétariat général des sanctuaires estime à plus de 6 millions le nombre de visiteurs de Lourdes par an – dont 1% sont malades. Sur les 50 dernières années, cela donne 300 000 000 visiteurs. Parmi eux, 1%, donc 3 millions de malades plein d’espoir. Retirons comme le fait la Commission de Lourdes les non-atteints de cancer, cela fait 30% des 3 millions, soit environ un million de personnes malades sans cancer, donc susceptibles de vivre un miracle pouvant être homologué.

Cinq miracles sur un million, c’est à peine supérieur à la moyenne des miracles en hôpitaux. La moyenne des hôpitaux étant une moyenne, on comprend bien qu’il y en a affichant des scores meilleurs, d’autres des scores moins bons, et que cela forme une sorte de résultat en cloche autour de la moyenne. Le résultat de Lourdes tombe dans les résultats de cette cloche, et les matheux avec leur langage diraient que son résultat n’est pas significatif. Il semble donc que Lourdes ne soit pas un endroit plus propice aux miracles que l’hôpital près de chez nous, et que si nous en avons l’impression, c’est parce que chaque cas Lourdais est fortement médiatisé.

Certaines mauvaises langues ajoutent que si l’on compte le nombre de gens qui se sont tués sur la route pour aller à Lourdes, alors il semble en fin de compte plutôt risqué d’y faire pèlerinage.

Une pente panglossienne

Quel est le lien entre le « chanceux » au Loto et les frères Bogdanoff ?

Quel est le trait commun entre Paul le poulpe et les créationnistes « scientifiques » ?

Quel est le fil conducteur entre le « miraculé » de Lourdes et la fameuse main invisible du marché ?

Il s’appelle Pangloss. C’est, peut être vous rappelez-vous, le precepteur de Candide, dans le conte de Voltaire. Il enseigne la métaphysico-théologo-cosmolonigologie, et répète à qui mieux-mieux qu’ admirablement qu’il n’y a point d’effet sans cause, et que, dans ce monde qui est le meilleur des mondes possibles, le château de monseigneur le baron était le plus beau des châteaux et madame la meilleure des baronnes possibles.

Pangloss dit surtout :

« Il est démontré (…) que les choses ne peuvent être autrement : car, tout étant fait pour une fin, tout est nécessairement pour la meilleure fin. Remarquez bien que les nez ont été faits pour porter des lunettes, aussi avons-nous des lunettes. Les jambes sont visiblement instituées pour être chaussées, et nous avons des chausses. Les pierres ont été formées pour être taillées, et pour en faire des châteaux, aussi monseigneur a un très beau château ; le plus grand baron de la province doit être le mieux logé ; et, les cochons étant faits pour être mangés, nous mangeons du porc toute l’année : par conséquent, ceux qui ont avancé que tout est bien ont dit une sottise ; il fallait dire que tout est au mieux. »….⁴.

Il s’agit d’une resucée de ce que le XIXe siècle a appelé la métaphore de l’horloger, que l’on doit au philosophe William Paley, et qui dit ceci

Le melon, le schtroumpf, les Bogdanoff

Les exemples de cette dérive panglossienne se comptent par centaines. Cela démarre par des trucs rigolos, comme le melon, qui, selon Jacques-Henri Bernardin de Saint Pierre « a été divisé en tranches par la nature afin d’être mangé en famille. La citrouille étant plus grosse peut-être mangée avec les voisins.» ⁵

Cela fait tout de suite moins rire quand des créationnistes chrétiens, juifs, ou plus récemment musulmans comme Harun Yayah viennent expliquer dans certaines écoles que l’œil humain, la synthèse des protéines, ou l’apparition de la conscience ne sont pas le produit d’une évolution mais d’un créateur et que l’Humanité a été créée par la volonté de Dieu. Cela fait vite frémir quand, de la même manière que le gagnant du Loto croit qu’il est élu par la Chance, Igor et Grishka Bogdanoff, ou Trinh Xuan Thuan le physicien bouddhiste croient l’univers trop finement réglé pour être le fruit du hasard physique (ce qu’ils appellent le fine-tuning, ce que d’autres appellent l’irréductible complexité).

 

On vient par cette occasion implanter une lecture finaliste des choses, l’idée qu’avant que toute chose démarre il y a comme un plan, une idée préconçue, une main invisible qui guide le processus et qui, implacablement, place chaque élément à sa juste place. C’est beau, c’est frais, c’est rassurant… mais c’est la fin de la connaissance, et c’est l’entrée des explications simples. Car finalement, dans quelque univers que l’on vive, même différent, on pourrait conclure la même chose : que tout est bien dans le meilleur des mondes, et que madame la baronne est la meilleure des baronnes possibles. Tout être vivant, qu’il soit Paul le poulpe, une bactérie ou un martien, pourrait conclure lui-aussi qu’il est le but ultime du Dessein Intelligent, d’une volonté cosmique. C’est irréfutable.

Dans un épisode des Schtroumpfs, on voit un des personnages décocher une flèche avec son arc les yeux fermés, puis chercher sa flèche. Une fois trouvée, il s’applique à peindre une cible autour du lieu de l’impact et… repart tout fier.

Pangloss et la fin des « possibles »

On trouve également Pangloss caché derrière l’idée que si le capitalisme s’est imposé, c’est qu’il le fallait, inexorablement, et que la main invisible du marché veille au grain. Pangloss passe par la porte quand les anciens rapports coloniaux affirmaient que puisque les Noirs étaient corvéables un peu partout, c’est qu’il devait y avoir un ordre naturel des choses. Pangloss se glisse dans la cuisine en instillant que si les femmes s’occupent des enfants et font le ménage, c’est qu’elles sont « faites » pour ça. Pangloss revient par la fenêtre quand il nous murmure à l’oreille que c’est dans l’ordre des choses que nous torturions d’autres animaux. Pangloss se tortille dans nos postes de télévision quand, on conclue parmi tous les possibles que tout est de la faute de la CIA, de la maffia russe, du lobby gay et lesbien, de la Mondialisation, des Francs-Maçons, des Sages de Sion… Éloge du scénario simple pré-écrit par des groupes supérieurs inaccessibles.

Le raisonnement des Bogdanoff des défenseurs du fine-tuning, des créationnistes, d’une bonne part des scénarios capitalistes, des théories racistes, sexistes et spécistes⁶ est le même : il vient essentialiser l’état actuel du monde comme une nécessité, comme une sorte de destin. Pangloss, que ce soit en jouant sur un tri des données ou sur un tri des « possibles », vient troquer la connaissance contre une croyance. C’est en cela qu’il est trompeur et séduisant : en faisant miroiter un finalisme facile, il évince notre capacité à repenser notre vie, nos actes et nos préjugés. Il nous gèle intellectuellement et nous nourrit de scénarios implacables, de karma, de mektoub, autant de chapes de plomb contre lesquelles on nous fait croire qu’on ne peut pas se révolter.

Richard Monvoisin

1 Statistiques disponibles ici.