Si quelqu’un vous vend un tableau mille euros, en vous assurant qu’il le revendra le lendemain 2000 euros, mais ne revient pas ledit lendemain : avez-vous perdu 1000 euros ? Ou avez-vous perdu 2000 euros ? Combien vaut une promesse de 1000 euros ?
Voici un travail pratique qui n’a pas encore été développé en cours par l’un.e d’entre nous, mais qui mériterait d’être testé car il fait le pont entre un escroc de Boston, des systèmes économiques pyramidaux et un débat moral captivant pouvant déborder, comme le fait Delahaye ci-contre, sur le système français des retraites.
Imaginons que quelqu’un propose un investissement à 100 % d’intérêts : vous lui donnez 10 euros, il vous en rend 20 en utilisant l’argent déposé par les clients suivants (il lui suffit d’ailleurs de proposer un rendement double des rendements connus du marché pour s’attirer de la clientèle et pour durer). Le système est viable tant que la clientèle afflue, attirée en masse par les promesses financières (et d’autant plus tentantes que les premiers investisseurs sont satisfaits et font une formidable publicité au placement). Les premiers clients, trop heureux de ce placement mirifique, reviennent dans la chaîne eux aussi, s’ajoutant à tous ceux qu’ils ont réussi à convaincre.
Le phénomène fait alors boule de neige, entretenu tant que l’argent rentre et permet de payer à 100 % les nouveaux investisseurs. L’organisateur prend une commission, bien compréhensible lorsque l’on voit les promesses qu’il fait, et qu’il tient. La chaîne peut durer tant que la demande suit la croissance exponentielle imposée par ce système, les clients arrivant par 2, 4, 8, 16, 32, etc. Lorsque la chaîne se coupe, la bulle éclate : tous les derniers investisseurs sont spoliés. Les gagnants sont ceux qui ont quitté le navire à temps et, surtout, l’organisateur.
Un système de Ponzi (« Ponzi scheme » en anglais) est un montage financier frauduleux qui consiste à rémunérer les investissements des clients essentiellement par les fonds procurés par les nouveaux entrants. Si l’escroquerie n’est pas découverte, elle apparaît au grand jour et s’écroule quand les sommes procurées par les nouveaux entrants ne suffisent plus à couvrir les rémunérations des clients1. Elle tient son nom de « Charles » Ponzi qui est devenu célèbre après avoir mis en place une opération basée sur ce principe à Boston dans les années 1920, même si le principe est bien plus vieux. Il est d’ailleurs narré dans une nouvelle de Charles Dickens de 1843 intitulée Vie et aventures de Martin Chuzzlewit.
Le mathématicien Marc Artzrouni modélise les chaînes de Ponzi en utilisant des équations différentielles linéaires du premier ordre.
Soit un fonds avec un dépôt initial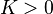 
, un flux de capitaux entrant de 
, un taux de rendement promis 
et un taux de rendement effectif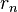 
. Si 
alors le fonds est légal et possède un taux de profit de 
. Si par contre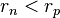 
, alors le fonds promet plus d’argent qu’il ne peut en obtenir. Dans ce cas, est appelé le taux de Ponzi.
Il faut aussi modéliser les retraits faits par les investisseurs. Pour ce faire, nous définissons un taux de retrait constant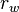 
, appliqué à tout temps 
sur le capital accumulé promis. Le retrait au temps vaut donc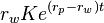 
. Il faut aussi ajouter les retraits des investisseurs qui sont arrivés entre le temps 
et le temps , à savoir ceux qui ont investit 
au temps 
. Le retrait pour ces investisseurs est donc de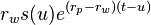 
. En intégrant ces retraits entre et et en ajoutant les retraits des investisseurs initiaux, nous obtenons: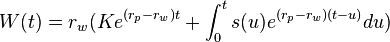 
Si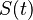 
est la valeur du fonds au temps , alors 
est obtenu en ajoutant à 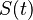l’intérêt nominal 
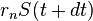, le flux de capitaux entrant 
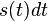et en soustrayant les retraits 
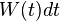. Nous obtenons donc 
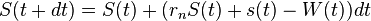, ce qui conduit à l’équation différentielle linéaire 
Voici un extrait de l’émission du 17 septembre 2012 de Continent Sciences, sur France Culture, avec Jean-Paul Delahaye, qui pose très bien la question suivante : dans quelle mesure le système de retraites françaises est-il une chaîne de Ponzi ?
Télécharger ou écouter :
Nonobstant deux imprécisions de Jean-Paul Delahaye :
– il confond Charles Dickens et Edgar Allan Poe dans ce passage
– il ne cite pas l’association philanthropique ayant déposé de l’argent chez B. Madoff. Et pour cause, il y en a plusieurs : les Fondations Carl et Ruth Shapiro, Jeffry et Barbara Picower, Sonja Kohn, The Mark and Stephanie Madoff Foundation, the Deborah and Andrew Madoff Foundation, America Israel Cultural Foundation, The American Committee for Shaare Zedek Medical Center, Hadassah, l’organisation des femmes sionistes et United Congregations Mesorah, une association religieuse qui est poursuivie pour 16 millions de dollars.