Nicolas Gauvrit nous le démontrait dans Graphiques, attention aux axes : plusieurs représentations graphiques distinctes peuvent être justes simultanément tout en provocant des perceptions très différentes de l’importance d’une variation ou d’une quantité. Le choix d’une représentation graphique peut donc influencer notre perception d’une situation donnée. Afin de limiter l’impact de cet effet sur notre jugement, il nous suffira de prendre une petite habitude peu coûteuse en temps : jeter un coup d’œil à l’échelle et à la valeur prise pour origine de l’axe des ordonnées.
Mais il s’avère que, de manière tout à fait similaire, une simple présentation de données chiffrées, qui pourrait sembler totalement objective, peut tout autant influer sur notre ressenti. Dans ce TP tout spécialement dédicacé aux « mathophobes », j’illustrerai ce phénomène sur un article du Dauphiné libéré intitulé Arnaques aux prestations sociales – Ces fraudes qui nous coûtent très chères et proposerai une parade efficace : confronter valeurs absolues et valeurs relatives.
Valeurs absolues et valeurs relatives.
La valeur relative est importante
Commençons avec un exemple fictif et imaginons qu’on me dise : » tu te rends compte, il y a 5 femmes dans cette entreprise ! « . Le ton de la phrase indique clairement qu’il y a là quelque chose de surprenant, mais hors contexte, si nous ne connaissons pas l’entreprise en question, on a bien du mal à savoir s’il faut s’étonner qu’il n’y ait que 5 femmes ou bien, au contraire, qu’il y ait autant de femmes. Dans cet exemple, mon interlocuteur me donne la valeur absolue du nombre de femmes. C’est une donnée en soi, probablement juste, mais qui ne me donne pas les informations nécessaires pour mesurer le côté » extra-ordinaire » de la situation.
S’il m’avait dit : » tu te rends compte, dans cette entreprise, il y a 50 salariés et 5 femmes ! » ou bien » tu te rends compte, il y a 5 salariés : ce sont 5 femmes ! « , j’aurais compris sa surprise, dans un sens ou dans l’autre. Cette nouvelle donnée me permet d’évaluer ce qu’on appelle la valeur relative du nombre de femmes, sous-entendu relativement au nombre de salariés : 10% dans le premier cas, 100% dans le second.
La valeur absolue est importante
Imaginons à présent que cette même personne me dise : « tu te rends compte, mon salaire n’a augmenté que de 0,5% alors que celui de ma collègue a augmenté de 3% ». On peut se dire à la vue des ces valeurs relatives que la situation est injuste. Mais avant de se faire un jugement, il est toujours bon d’aller chercher quelques renseignements supplémentaires : mon interlocuteur dit avoir un salaire net de 10 000 euros/mois et sa collègue déclare 1 000 euros/mois. Je peux alors calculer la valeur absolue de leur augmentation – ici c’est la valeur en euros : 500 euros par mois pour mon ami et 30 euros pour sa collègue. En valeur absolue, l’injustice apparaît dans l’autre sens.
Les valeurs relatives et absolues sont justes toutes les deux, mais provoquent un ressenti opposé.
On retiendra de ces deux exemples une chose fondamentale : valeur relative et valeur absolue sont aussi importantes l’une que l’autre pour se faire un avis et il faudrait pouvoir exiger systématiquement qu’on nous donne les deux, sous peine de laisser à la personne qui défend sa thèse la possibilité de jouer sur notre ressenti en choisissant la valeur qui va le plus dans son sens.
Titre

Titre + sous-titre

Extrait n°1
1er extrait + sous-titre : la fraude aux prestations sociales est estimée entre 8 et 10 milliards d’euros (valeur absolue).
Quel sentiment cela provoque-t-il ?
Pour établir la valeur relative, il nous manque la quantité de prestations sociales versées au total. L’article est long, mais en cherchant bien, on finit par trouver – si cette donnée n’avait pas été présente, on aurait pu aller la chercher dans le rapport de la Cour des comptes.

Extrait n°2
Valeur relative de la fraude par rapport à l’ensemble des prestations sociales : (8/450)*100 = 1,8%.
On pourra remplacer cette valeur relative dans le sous-titre et le premier extrait. Ressentez-vous la même chose ?
Un autre passage a attiré mon attention. Le voici.

Extrait n°3
Pourquoi m’arrêter sur ce passage ? Parce qu’à la première lecture, j’avais compris ceci :
Nombre d’allocataires contrôlés : 10 000
Difficile de se faire une idée de la situation avec ces chiffres « bruts », mais un rapide calcul de… valeur absolue démontre qu’il y a très probablement anguille sous roche :
Fraude moyenne par allocataire (ou valeur relative) : 675 000 000 / 10 000 = 67 500 euros/allocataire
L’ordre de grandeur est complètement déraisonnable, d’autant plus si l’on se souvient que le sous-titre nous assure que la plupart des fraudeurs sont des RMIstes. Des RMIstes qui arriveraient à frauder plus de 67 000 euros, c’est très étonnant. Un peu trop… Je suis donc allée vérifier à la source, dans le rapport des la Cour des comptes, et j’y ai trouvé ceci
| Rapport de la Cour des comptes – Septembre 2009 – p????Les travaux les plus avancés d’analyse d’échantillons ont été menés dans la branche famille. La CNAF a réalisé en effet, au second semestre 2009, une évaluation des fraudes, à partir d’un échantillon représentatif de plus de 10 000 dossiers. Avec l’inévitable marge d’incertitude[…], les travaux réalisés semblent constituer une première base de travail solide qui permet de donner un ordre de grandeur de la fraude totale dans la branche famille, qui atteindrait environ 675 M€ par an […] |
Ce petit mot, « totale », avait disparu dans l’article du Dauphiné Libéré. Il s’agit probablement d’une imprécision, mais toute influence n’est pas nécessairement « voulue » ou décidée. Il y a une différence de taille entre « on a repéré une fraude de 65 millions d’euros sur 10 000 allocataires » et « on a repéré une fraude de 65 millions d’euros sur l’ensemble des allocataires ».
Pour obtenir la valeur exacte de la fraude moyenne par allocataire, il nous faut le nombre total d’allocataires de la branche famille, nombre que je n’ai pas trouvé.
-> donc RSAste : fraude 70% * 675000000= 472 Millions
nombre de RSAstes (2009) : 1,7 million
moyenne : 277 euros/an/allocataire -> erreurs ?



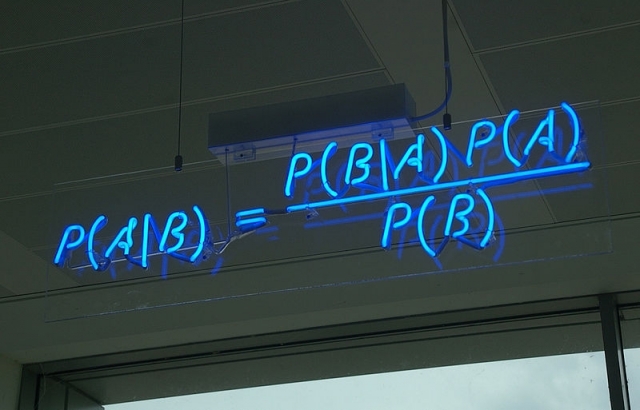

 et d’en déduire que la cause principale de ces cancers est le tabagisme. Attention, si vous en tirez cette conclusion, vous êtes en train de toucher du doigt le problème des probabilités inversées : ce n’est pas cette statistique seule qui permet d’inférer un lien de cause à effet entre tabagisme et cancer. Car on pourrait très bien trouver, en cherchant un peu, que 99% des personnes décédées portaient des sous-vêtements, sans pour autant en conclure à un lien causal direct entre porter un slip et mourir d’un cancer des poumons. Autrement dit, la probabilité de porter des sous-vêtements sachant que l’on est mort d’un cancer ne nous donne aucune information sur la dangerosité ou le risque de cette pratique.
et d’en déduire que la cause principale de ces cancers est le tabagisme. Attention, si vous en tirez cette conclusion, vous êtes en train de toucher du doigt le problème des probabilités inversées : ce n’est pas cette statistique seule qui permet d’inférer un lien de cause à effet entre tabagisme et cancer. Car on pourrait très bien trouver, en cherchant un peu, que 99% des personnes décédées portaient des sous-vêtements, sans pour autant en conclure à un lien causal direct entre porter un slip et mourir d’un cancer des poumons. Autrement dit, la probabilité de porter des sous-vêtements sachant que l’on est mort d’un cancer ne nous donne aucune information sur la dangerosité ou le risque de cette pratique.

