Author: Denis Caroti

Former l’esprit critique : ressources pour enseignant·e·s

Depuis juillet 2020, je participe à une rubrique consacrée à l’esprit critique dans la revue Sciences & Pseudosciences éditée par l’Association Française pour l’Information Scientifique (AFIS). J’y explore notamment les différentes facettes de la formation à l’esprit critique des enseignant·e·s ainsi que les questions en lien avec l’éducation à l’esprit critique. Vous trouverez ici l’ensemble des articles déjà publiés et mis en ligne par l’AFIS, ainsi qu’une présentation de ceux-ci, facilitant leur lecture et la compréhension générale de ce travail.

Pourquoi enseigner l’esprit critique ?

Dans ce premier article, je présente le cadre général de l’éducation à l’esprit critique, ses objectifs et enjeux, la définition de l’esprit critique et ses différentes dimensions. J’aborde également la question des formations à l’esprit critique pour les enseignant·e·s. En effet, si depuis 2015 celles-ci se développent fortement, certaines sont ancrées dans le travail du Cortecs et abordent spécifiquement la question de l’épistémologie, des démarches scientifiques, de la zététique et de l’autodéfense intellectuelle.

SPS333_Pourquoi-enseigner-lesprit-critiqueTélécharger

Former les enseignant·e·s à enseigner l’esprit critique

Dans ce deuxième article, je présente plus spécifiquement le contenu des formations à l’esprit critique pour les enseignant·e·s. En insistant d’abord sur le sens et les objectifs que l’on donne à ces formations, je reviens sur le juste équilibre à trouver entre un contenu ciblant des ressources pédagogiques à destination des enseignant·e·s et des activités permettant avant tout de former des individus. En effet, si l’on souhaite que soit transposée en classe cette éducation à l’esprit critique, il faut d’abord et avant tout que nos collègues s’approprient et trouvent un intérêt à aborder ces thématiques. Je présente également les différents « modules » que contient cette formation et décris rapidement un premier temps de « remue-méninges » pour travailler sur la délicate distinction entre science, croyances, connaissances et pseudosciences.

SPS334_Former-les-enseignants-à-lECTélécharger

Croire et savoir

Cet article développe ce qui a été décrit à la fin du précédent : comment aborder la question de la distinction entre croyances et connaissances ? Comment, en tant qu’enseignant·e, s’y retrouver et être capable de poser clairement les choses face aux élèves ? J’y évoque quelques « astuces » et mises en œuvre pour travailler sur ce sujet : d’abord, en distinguant la capacité à remettre en question (ou pas) nos croyances et connaissances, puis en relevant les différences entre nos croyances (et connaissances individuelles) et les connaissances scientifiques. L’idée est de sortir d’une vision simpliste de la distinction entre croyances et connaissances, tout en donnant des moyens aux enseignants de répondre concrètement aux élèves sur ces questions.

SPS335_Croire-et-savoirTélécharger

La hiérarchie des niveaux de preuve

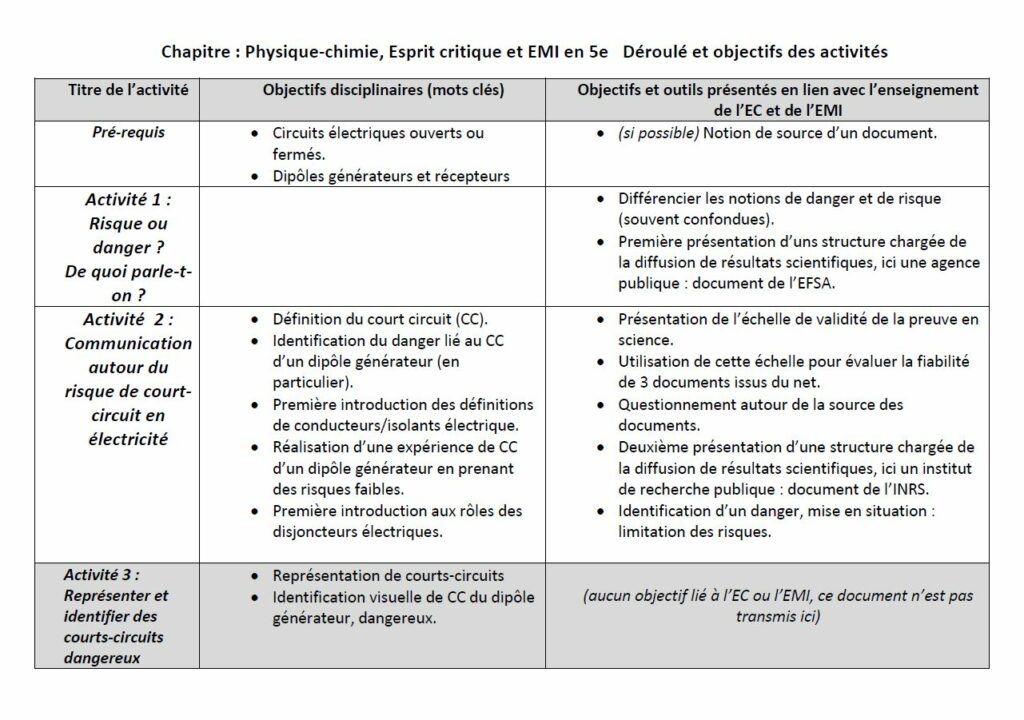
Pour continuer sur le lien entre épistémologie et esprit critique, cet article aborde la difficile tâche d’évaluer la fiabilité des preuves étayant une affirmation. En effet, parvenir à ajuster notre niveau de confiance face à une information passe par différents aspects, dont notamment notre capacité à savoir si les éléments fournis pour l’étayer sont suffisants. J’y présente d’abord ce qu’est une preuve puis j’y discute l’intérêt et les limites d’utiliser une échelle des niveaux de preuve, ainsi que les différentes manières d’aborder ces aspects au niveau pédagogique.

SPS336_Hierarchie-niveaux-preuveTélécharger

Bases théoriques et indications pratiques pour l’enseignement de l’esprit critique

Dans cet article, j’ai le plaisir d’interviewer Elena Pasquinelli, chercheuse, formatrice et membre du Conseil Scientifique de l’Éducation Nationale, ayant en charge les travaux du groupe n°8 consacré à l’esprit critique. Elle revient notamment sur la publication et contenu du rapport produit par ce groupe en 2021 et fournissant pour la première fois un corpus théorique et pratique pour l’enseignement de l’esprit critique. Cet article permet ainsi d’avoir un bon résumé du contenu du rapport qui, si l’on devait le résumer en une phrase, précise l’importance d’identifier certains critères opérationnels et concrets, permettant aux enseignants de savoir comment orienter efficacement leur cours dans l’objectif d’y incorporer des éléments propres à l’éducation à l’esprit critique.

SPS337-Interview-Elena-PasquinelliTélécharger

Le niveau d’étude peut-il aggraver les préjugés ?

Une question souvent posée en lien avec l’esprit critique et son enseignement concerne le rôle des connaissances. Celui-ci est indéniable : l’esprit critique ne s’exerce pas à vide. Mais ces connaissances ne suffisent pas pour évaluer l’information et reconnaître si l’on est en face d’un contenu biaisé ou frauduleux. Parfois, elles peuvent même entretenir nos préjugés erronés. Dans cet article, je reviens sur les travaux conduits par différents chercheurs étudiant le lien entre le niveau de connaissances générales (ou même le niveau d’études) et les capacités cognitives ainsi que le niveau de croyances non fondées. Par exemple, certaines recherches suggèrent que, sur des sujets médiatiquement controversés ou très contestés (réchauffement climatique, théories de l’évolution, recherche sur les cellules souches), le niveau d’études, même s’il s’agit d’études scientifiques, est corrélé à un renforcement des préjugés idéologiques. Il ne fait qu’aider à confirmer les opinions préexistantes des individus, même lorsqu’elles sont fausses…

SPS338_Niveau-étude-et-préjugésTélécharger

Une partie de l'excellente équipe de la médiathèque d'Aubagne et des services jeunesse et prévention

Ateliers Esprit critique et autodéfense intellectuelle

Une partie de l'excellent équipe de la médiathèque d'Aubagne

Depuis 2019, le Cortecs travaille avec la médiathèque d’Aubagne et les services jeunesse et prévention de la Mairie d’Aubagne pour élaborer et construire des ateliers sur la thématique de l’esprit critique et de l’autodéfense intellectuelle à destination des élèves des collèges et lycées de l’académie d’Aix-Marseille. Après plusieurs journées de formations, les animateurs sont intervenus régulièrement auprès des classes sur différentes thématiques. Ce travail a permis de repenser, actualiser, mais aussi de créer des ateliers permettant d’aborder des « classiques » de la zététique : effet Barnum, principe de parcimonie, échelle des preuves ou coïncidences, autant de sujets que les élèves ont pu découvrir grâce à toute l’équipe qui partage aujourd’hui ses productions et ressources avec nous. Un grand merci et surtout bravo à eux pour tout cela !

Présentation du projet

Objectifs, compétences travaillées, organisation des séances : ce document présente le projet dans son ensemble.

Description des ateliers

Vous trouverez ci-dessous les différents ateliers proposés ainsi que tous les contenus utilisés et que toute l’équipe partage avec plaisir. Le dossier complet est ici. Merci à eux !

Jouer à débattre

Jouer à débattre (atelier créé par L’arbre des connaissances). Le thème choisi a été l’humain augmenté. Le but étant d’amener les élèves à argumenter et à prendre conscience de la complexité insoupçonnée des sujets de société.

Atelier philo

S’exercer à réfléchir, apprendre à discuter, écouter, raisonner et respecter l’autre avec cet atelier philo.

Fake news

Cet atelier correspond à l’atelier « Le vrai du faux » (créé par le CRIJ). L’objectif est d’appréhender la complexité à évaluer la fiabilité des informations et de se poser les bonnes questions pour y parvenir.

Test de personnalité : l’effet Barnum

Un « classique » de la zététique où l’on va reproduire l’expérience de Bertram Forer sur l’effet qui porte son nom (mais aussi celui d’effet Barnum) : un atelier mettant en scène un faux test de personnalité à évaluer par les élèves. Vous retrouverez dans ce dossier les fiches, vidéos et autres documents utilisées pour mener à bien cet atelier.

Principe de parcimonie et rasoir d’Occam

Comment travailler sur le principe de parcimonie avec les élèves ? Comment faire découvrir cet outil de tri des hypothèses et ses limites ? Le dossier avec tous les éléments se trouve ici !

Échelle des preuves et curseur de confiance

Un atelier repris de l’activité proposée dans l’excellent ouvrage publié par nos collègues de La main à la pâte, et qui permet de travailler avec les élèves sur la notion de preuves et de confiance. Tout le dossier est à retrouver ici.

Coïncidences…

Un atelier sur la notion de coïncidences : y a-t-il forcément un sens à donner à ces conjonctions d’événements intrigants et qui nous paraissent si étranges…? Le dossier complet ici !

Bilan

Voici quelques retours concernant les ateliers

Au niveau de l’enchainement des ateliers, commencer par Jouer à débattre permet de créer une bonne relation avec les élèves qui se retrouvent dans une situation de jeu qui les change de leur quotidien. L’atelier sur les fake news comme les suivants sont un peu plus scolaires, contenant plus d’explications (un peu plus descendant) : les élèves sont mis en activité, mais cela demande toujours une implication de leur part qui dépend bien entendu de beaucoup de paramètres.

On a pu remarquer que les ateliers Jouer à débattre, effet Barnum et rasoir d’Occam ont très bien fonctionné : le mélange entre travail de groupe, débat et effet de surprise motive toujours les élèves et retient leur attention.

Concernant l’atelier sur l’effet Barnum, il faut bien penser à faire attention aux contacts possibles entre élèves pour éviter qu’ils comprennent le truc.

L’atelier sur l’échelle des preuves est aussi à améliorer sur la manière de l’animer : nous proposons d’y ajouter davantage de moments d’interactions variées.

Loïc Massaïa, imperturbable mais toujours pertinent !

Un merci très spécial à Loïc Massaïa pour le soutien, l’expertise et l’aide apportée tout au long de ces ateliers, mais également pour le partage des documents !

Physique-chimie, esprit critique et EMI

Julien Machet est professeur de Physique-Chimie dans l’académie de Lyon, et exerce au collège Saint André de Corcy. Il est également membre du Groupe de ressources académique « Esprit critique ». Julien a déjà publié son travail sur le tri de l’information (voir ici) et il nous propose à présent de partager une séquence entière, à destination des élèves de 5ᵉ, et qui vise à comprendre comment la médiatisation de contenus scientifiques, notamment sur les notions de risque et de danger, peut servir l’enseignement de savoirs disciplinaires (ici, l’électricité et la chimie). Bravo et merci (encore) à lui pour ce travail précieux !

Présentation rapide

La séquence abordée ici mélange des objectifs de transmission de savoirs disciplinaires d’électricité et de chimie avec des objectifs propres à l’enseignement de l’esprit critique et de l’éducation aux médias et à l’information. Elle est enseignée en classe de 5e.

Déroulé des activités et descriptifs des objectifs (cliquer sur l’image pour voir tout le document)

Lever la confusion entre danger et risque est présenté ici comme un véritable objectif, en soi, de l’enseignement de l’esprit critique. En effet, de nombreux débats de société liés aux questions de santé sont perturbés par les confusions communes entre l’existence d’un danger avéré et l’évaluation d’un risque (fort ou faible) et par la non-priorisation de traitement des risques forts face aux risques faibles.

Positionnement dans une progression pédagogique

Ce chapitre s’intitule, pour les élèves de 5e concernés : « Les scientifiques parlent au grand public ; exemple des dangers et des risques en physique chimie », il est inclus dans un thème intitulé « Communiquer en science » et répond à un autre chapitre centré sur un exemple de langage « de spécialistes » lui-même intitulé « Les scientifiques parlent aux scientifiques ; exemple de la schématisation en électricité ».

Documents à télécharger

Julien met à disposition l’ensemble de ses documents utilisés pour cette séquence, en format modifiable et pdf.

  • Le document de présentation de toute la séquence :

Télécharger

Pour tout contact : julien.machet-at-ac-lyon.fr

Tri de l'information et enseignement de l'esprit critique : une carte pour s'y retrouver

Julien Machet est professeur de Sciences Physiques et Chimiques dans l’académie de Lyon. Travaillant en collaboration avec le CORTECS et notamment notre collègue Denis Caroti depuis plusieurs années, il forme également les enseignants sur la thématique « Analyse de l’information et esprit critique ». Par ailleurs, il développe dans ses cours un enseignement de l’esprit critique incorporé à ses contenus disciplinaires. Julien a ainsi créé une carte conceptuelle à destination des élèves (et des enseignants), permettant de visualiser rapidement les outils méthodologiques d’analyse de l’information. Il nous présente ici la genèse de cette carte, ses objectifs ainsi que son contenu et ses réflexions sur ce sujet. Bien entendu, cet outil mérite d’être encore amélioré et adapté, mais c’est une base utile, fruit d’essais et erreurs fertiles. Bravo et merci à lui pour ce travail précieux !

Mise à jour (avril 2021)

Les cartes méthodologiques d’analyse de l’information ont été mises à jour et sont téléchargeables en format modifiable (voir dernière partie Enseigner l’esprit critique)

Objectifs

Deux grilles de lecture, sur deux plans différents : analyse de l’information et construction des connaissances & enseignement de l’esprit critique

  • Premièrement, cette carte présente différents axes de questionnement permettant de se positionner (ou non) face à une information, quelle qu’elle soit. De plus, elle permet de présenter en quoi la construction méthodologique et collective du savoir en sciences doit prendre en compte ces axes d’analyse de l’information, et les risques spécifiques qui y sont associés.
  • Deuxièmement, elle peut permettre à l’enseignant d’expliciter aux élèves en quoi les activités faites en classe permettent de se donner des outils de tri de l’information, de construction du savoir. Elle peut donc servir de base à la conception d’un enseignement de l’esprit critique à travers des enseignements disciplinaires classiques.

J’évoquerai donc ces différentes utilisations de la carte et j’en donnerai ensuite une version pour les élèves.
Précaution : j’utilise ici une définition large du mot information, je n’ai pas choisi de circonscrire ce mot à un fait vérifié qui intéresse un grand nombre de personnes comme cela est fait, par exemple, sur l’activité «  Qu’est-ce qu’une info ?  » publiée sur le site du CLEMI. Ainsi analyser une information signifie ici analyser une donnée, une affirmation qui nous parvient, quelle que soit sa forme.

Introduction

Cette carte conceptuelle (ou gros schéma…) à destination des enseignants intéressés par le tri de l’information et son enseignement est née d’un échange avec ma collègue Cécile Dussine (Sciences Physiques) qui a créé une activité d’introduction aux cours de sciences physiques en 6ème. Une version de cette activité devrait être publiée en 2019 dans l’ouvrage «  Développer l’Esprit critique : Outils et méthodes », aux éditions CANOPÉ, mais je vais en décrire les principales étapes sans entrer dans le détail.

  • Le professeur donne tout d’abord aux élèves deux résumés de deux textes issus de sites web existants. L’un porte une information vraie (validée par un consensus scientifique), l’autre une information erronée (sans que l’on sache si c’est intentionnellement ou non).
  • Les élèves sont ensuite amenés à se positionner face à ces affirmations. Le professeur met en lumière les désaccords au sein de la classe : certains élèves doutent du contenu de ces textes
  • Le professeur apporte ensuite une information dérangeante : un des deux textes donne une information erronée ! Plusieurs questions se posent alors :

Lequel est faux ? Comment faire pour le savoir ? Quelle(s) méthode(s) appliquer ?

  • S’ensuit la distribution des documents complets ainsi que leur étude selon différents axes. On demande alors aux élèves de se positionner à nouveau, de manière bien plus argumentée, cette analyse conduisant à un avis quasi-unanime sur le contenu des deux textes.

La carte suivante est donc née de cette dernière question (Quelle(s) méthodes appliquer ?) et de la volonté de clarifier et d’organiser les réponses possibles pour moi, pour les enseignants mais aussi pour les élèves.

CorteX_Carte_Analyse_information_Méthodologie_Enseignants
Carte méthodologique : analyse de l’information pour enseignants, par Julien Machet

Première utilisation : ANALYSER une information ou une affirmation : des axes de questionnement

Question préalable : a-t-on bien compris quelle était cette information ?

Pour cela un bon exercice est de voir si on arrive à résumer l’information en une phrase ou deux. Attention à ne pas se fier au titre (s’il y en a un) : il ne constitue pas forcément un résumé fiable.

Premier axe d’analyse : ÉTUDE DU CADRE

  • Une information nous arrive dans un cadre donné, qu’on le veuille ou non : elle n’arrive de facto pas seule. Elle ne peut être isolée de son contexte présent et de ce que l’on sait déjà. J’entends par cadre tout d’abord le cadre médiatique. On peut ainsi penser qu’une information aura un impact ou une réception différente si elle nous parvient en période électorale ou non, si elle suit ou en précède une autre, si elle est très médiatisée ou non. Je distingue ici le cadre médiatique de la source de l’information, qui mérite un travail approfondi en soi.
  • Lien avec nos connaissances initiales : une information vient s’imbriquer plus ou moins bien avec l’ensemble de nos connaissances actuelles. Il est donc intéressant de se demander si cette information remet en question des savoirs que l’on a déjà considéré comme acquis, et si elle remet en question des actes ou des choix que nous avons faits ? On pense évidemment à éviter le plus possible le biais de confirmation dont nous sommes toutes et tous victimes.
  • J’ai également placé sous cet axe de l’étude du cadre, un grand point un peu fourre-tout intégrant les liens personnels ou relationnels, sans se limiter aux relations affectives, et que l’on peut avoir avec la source de cette information, son auteur, avec le cadre en général ou encore avec la thématique, le sujet de l’information. En effet, avant même de savoir ce qui est dit, il faudrait avoir conscience de notre état émotionnel et affectif, et de ses effets sur le jugement que l’on porte sur l’information reçue. Ne sommes-nous pas déjà un peu d’accord ou pas avec le contenu de l’information avant même d’avoir lu son contenu, du simple fait du cadre médiatique ? Avoir en tête que notre avis va dépendre en partie de notre « proximité » idéologique avec le média qui transmet l’information est déjà un pas de côté nécessaire pour analyser celle-ci. À noter que ce lien au cadre n’est pas forcément un lien affectif et qu’il peut aussi être une confiance que l’on accorde à un cadre donné : si je choisis d’aller suivre un cours dans telle université réputée, il peut être efficace d’accorder au départ du crédit à ce qui va être dit.
  • Cas particulier d’une information reçue « à l’école » : l’étude du cadre scolaire et du cadre de la classe en particulier me semble un axe de travail inévitable. En effet, donner aux élèves un texte contenant une information fausse, ou simplement une information dont la fiabilité doit être étudiée est un acte qui bouscule le cadre « de ce qui se fait en classe » (au moins aux yeux des élèves). De plus, le professeur peut se sentir en difficulté, ou peut estimer prendre des risques, en incitant les élèves à adopter un regard critique sur l’information reçue. En effet il est possible, et souhaitable, que l’élève continue à avoir ce regard critique après l’activité … Notre cours passera-t-il l’examen de ce regard ? Et celui d’un autre collègue ? Avons-nous, en tant qu’enseignant·e, le temps et l’envie de tout justifier ? En sommes-nous capables ? Est-ce souhaitable ?
    Il convient donc à mes yeux d’utiliser simplement la grille d’analyse de la pensée critique pour améliorer et transformer nos cours (évidemment) mais aussi pour apprendre à justifier, à légitimer la confiance que les élèves peuvent avoir dans le contenu des enseignements (cf. conclusion de l’article). Si la parole donnée par l’enseignant·e n’est pas égale à celle de l’élève en ce qui concerne l’expression de faits scientifiques, c’est qu’elle se fait l’écho d’une démarche de construction des savoirs, démarche collective, exigeante et régulée.  La confiance que peut avoir l’élève est donc raisonnée et raisonnable. A ce titre, on est loin du registre de l’obéissance aveugle ou de la révélation.
    La démarche de construction de la connaissance est une démarche où seules la validité des preuves et la pertinence des arguments sont censées entrer en compte. Par conséquent, travailler et expliciter cette démarche en classe c’est aussi installer un cadre collectif où l’humilité, l’honnêteté, l’exigence et la bienveillance sont des valeurs qui guident les propos tenus et les relations humaines. Il faut donc jongler entre, d’une part le fait d’apprendre à être dans un cadre collectif, où chacun se doit d’être à l’écoute et respectueux de la parole de chacun (et cela ne se fait pas spontanément), et d’autre part le fait que l’enseignant·e « fasse autorité » dans la transmission du savoir.
    Au delà de l’équilibre que chacun doit trouver, au delà des évolutions nécessaires de notre système éducatif, il apparaît indispensable que l’élève puisse faire la différence entre un argument imposé via un biais d’autorité, et la parole d’un consensus d’expert·e·s dont on peut accepter raisonnablement qu’il fasse autorité. La limite est souvent subtile, mais les situations où les mécanismes de dominations et les positions d’autorités sont utilisées pour simplement clore la réflexion ou la discussion sont, elles, monnaies courantes.
    Il serait dommage que l’école soit un lieu où l’enfant prenne l’habitude de subir et d’arrêter de réfléchir… Travailler sur le cadre de la classe et la démocratie scolaire est certainement un point indispensable d’un réel enseignement de l’esprit critique. Vaste chantier !

Deuxième axe d’analyse : ÉTUDE DE L’ENJEU

Si cette information est vraie ou fausse, qu’est-ce que ça change pour moi, pour mes proches ou pour le monde en général ? Le principe journalistique de la loi de proximité, permet de relativiser, si cela était nécessaire, le fait que l’on juge spontanément et correctement l’enjeu d’une information. Si l’on ajoute à cela la complexité de notre monde et de son fonctionnement, il peut être très difficile de cerner l’enjeu (ou l’importance) de certaines informations. À noter tout de même que l’on peut émettre l’hypothèse suivante à peu de frais : plus on connait et on comprend notre monde, plus on est à même d’évaluer correctement l’enjeu d’une information.
Ainsi, de façon plus ou moins consciente, nous évaluons certainement l’enjeu (et donc l’intérêt) de l’information reçue : si celui-ci nous semble suffisamment faible, alors il est fort probable que nous n’en fassions pas une analyse poussée. Étant donné le nombre d’informations qui nous parvient chaque jour, il serait bien entendu utopique de s’interroger sur chacun d’entre elles, ce mode de fonctionnement (le tri par intérêt) est donc assez habituel. Pour autant, il est nécessaire d’en avoir conscience : nous laissons bien souvent de côté l’analyse d’informations que nous jugeons sans intérêt.
Par contre si l’enjeu est grand, si cette information nous parait importante, si l’affirmation n’est pas ordinaire alors nous devrions pousser plus loin notre analyse. Ceci fait écho à la maxime de Hume souvent résumée en zététique par « une affirmation extraordinaire nécessite des preuves plus qu’ordinaires ».
Dans notre vie quotidienne nous ne passons souvent pas le cap d’une analyse grossière et plus ou moins consciente du CADRE et de l’ENJEU. Il est probable que nous décidions à ce stade, la plupart du temps, de prendre en compte ou non une information. Or il faudrait, par souci « d’hygiène mentale », réaliser ces deux analyses plus finement et, si l’enjeu potentiel est important, décider alors de pousser l’analyse plus loin avant de se positionner ! Et dans ce cas, la suspension du jugement chère aux sceptiques ne devrait-elle pas être que provisoire ? C’est pourquoi même si je ne vois pas d’ordre chronologique évident selon lequel on devrait appliquer ces différents axes d’analyse, commencer par travailler à conscientiser ces deux là me semble un préalable tout à fait raisonnable et justifié.

Troisième axe d’analyse : Étude de LA SOURCE

Je ne m’étendrai pas sur le sujet, non pas qu’il ne soit pas important, mais il est très souvent traité quand on parle d’analyse de l’information. On peut facilement trouver des méthodes sur ce sujet. Par exemple le 3QPOC pour les sites internet. Il faut évidemment penser à vérifier si l’on peut recouper l’information, trouver d’autres sources (à évaluer également) qui disent la même chose.

Quatrième axe d’analyse : Étude de la FORME

On devrait dire étude des formes, car derrière chaque format de communication (texte écrit, discours oral, image, graphique et tableau, graphisme et mise en page, vidéos, etc.) se cachent des règles de langage, des registres, des styles, des codes culturels explicites ou implicites, des sous-entendus  et parfois des moyens de manipuler le futur récepteur de l’information ! L’étude de la FORME du support de l’information, des langages utilisés et de leur réception est évidemment une source infinie de créativité et d’analyse critique. Quelques exemples d’outils permettant de décrypter cela : effet puits, effet Impact,  images mensongères, cadrage en photo, graphiques. On ne manquera pas d’ailleurs de noter que l’étude succincte de la forme de la carte donne quelques indices sur les talents graphico-informatiques de l’auteur de ses lignes. Ce qui n’arrêtera cependant pas le lecteur perspicace parcourant ces lignes…

Cinquième axe d’analyse : Étude du FOND, du propos, du sens

Je décompose ici l’étude du FOND en trois points :

  • L’étude du sens des mots utilisés, des concepts manipulés : sommes-nous d’accord sur leur définition ? Sur leur connotation ? Sont-ils utilisés de façon rigoureuse ? Les concepts manipulés sont-ils sortis abusivement de leur champ disciplinaire ?
  • L’étude des preuves, des références : à quoi se réfère l’affirmation ? Quelles sont les preuves explicites ou sous-jacentes qui viennent appuyer cette information ? Pour cela il est utile de se référer à l’échelle du niveau de preuve en science, illustrée avec talent ici.
  • L’étude des raisonnements, la logique : une fois les mots et les preuves posés, comment sont-elles ou sont-ils mis en rapport ? Comment les arguments sont-ils construits ? À noter que dans le Petit recueil de 25 moisissures argumentatives, on dénombre 5 erreurs classiques de logique « pure » (biais de généralisation, raisonnement panglossien, etc). De manière plus générale, la liste des biais cognitifs qui nous poussent à penser que quelque chose de faux est vraisemblable est très longue, voir par exemple ce codex fait en 2016 et résumant ceux-ci.

Ces axes d’analyse nous permettent de nous positionner de façon argumentée sur la vraisemblance de l’information reçue. Afin de mieux visualiser une échelle allant de l’information assurément fausse à l’information assurément vraie en passant par plusieurs niveaux de doute plus ou moins favorable à l’information, on peut utiliser une sorte de « curseur de vraisemblance » (l’original par Henri Broch ici) comme proposé sur la carte. L’important à mes yeux est de pouvoir se positionner de façon argumentée, et ce, en invoquant des résultats, plus ou moins poussés, des études précédentes sans forcément avoir étudié en détail tous les axes d’analyse !
Exemples de positionnement :

  • La source me semble fiable (auteur connu et respecté qui s’exprime sur son sujet) mais la forme est un peu bizarre (le graphique n’a pas d’axes clairs), et sur le fond il y a un mot qui me semble mal utilisé. Je trouve l’info plutôt fiable, au niveau 4/5.
  • L’enjeu est faible et j’ai plutôt confiance dans l’auteur (qui a écrit tel livre que je juge très bon): je vais considérer ça comme fiable : 3/5
  • Cette affirmation est en contradiction totale avec ce que je sais de la physique de base : information pas du tout fiable : 0/5.

En effet, au-delà de l’outil d’analyse individuelle, pouvoir se positionner de façon argumentée c’est pouvoir exposer sa pensée aux critiques (que l’on espère argumentées et bienveillantes) d’autres personnes, c’est donc pouvoir débattre de façon raisonnée et se laisser la possibilité de construire progressivement un avis plus construit, mieux argumenté et évitant ainsi d’autres erreurs de positionnement.
On peut également décider de suspendre son jugement, d’estimer que l’on n’a pas assez d’éléments pour se positionner, ou que les critères d’évaluation sont contradictoires. En cas de doute ou de suspension du jugement, si l’enjeu est important : il faudrait certainement entreprendre de se renseigner davantage sur le sujet.
On peut aussi dire qu’une information jugée fiable devient une nouvelle connaissance à condition d’avoir appliqué scrupuleusement tous les axes et les biais associés : la validation du savoir en science est une démarche collective, méthodique et exigeante. Apprendre à analyser une information c’est donc aussi se donner des outils méthodologique dont les principes sont les mêmes que ceux d’un chercheur.

Seconde utilisation : ENSEIGNER l’esprit critique. Expliciter les outils méthodologiques sous-jacents

Lors de l’activité menée en 6ème et évoquée en début de présentation, seuls trois axes d’analyse sont présentés aux élèves : la source, le sens des mots et les preuves. Les trois analyses convergent toutes dans le même sens mais c’est surtout l’étude du sens des mots qui nous permet de trancher, car le texte contenant de fausse informations utilise abusivement des concepts scientifiques de base.
Une fois la partie analyse de l’activité terminée, plusieurs points sont abordés en conclusion et apparaissent en général comme évidents pour élèves :

  • Se mettre d’accord sur le sens des mots est indispensable.
  • Il faut analyser la source d’une information.
  • Il va falloir déterminer quand une preuve est fiable ou non.

Et ce afin d’acquérir des savoir-faire, des techniques permettant de mieux trier l’information, de « ne pas se faire avoir ».
Ainsi, à chaque fois que de nouveaux mots de vocabulaire seront introduits, il sera pertinent de faire ressentir aux élèves (via la construction didactique de l’activité) l’aspect nécessaire de ces mots. Ceux qui ont plusieurs sens, ou dont le sens change en fonction du cadre (poids/masse par exemple) seront également présentés en lien avec cette activité introductive.
Pour le travail sur les sources, j’essaie de m’astreindre à deux règles en cours de sciences physiques :

  • Toujours citer la source, toujours évaluer sa fiabilité (même en se contentant souvent de : fiabilité du document selon le professeur : très bonne)
  • Donner parfois des documents aux sources douteuses et aux informations partiellement erronées.

Pour le travail sur les preuves, apprendre à évaluer une preuve et à construire des preuves via l’expérimentation est un travail continu en cours de sciences physiques.
En rajoutant l’étude de la FORME, des langages, j’obtiens une version de carte destinée à être collée dans les cahiers (l’utilité de ce document dans leur cahier est inconnue à ce jour) et surtout à être affichée en classe de manière à pouvoir s’y référer fréquemment en cours. Voici la version élève de cette carte :

Carte méthodologique : analyse de l’information pour les élèves par Julien Machet

J’ai choisi de ne pas détailler ici le CADRE et l’ENJEU mais de les laisser pour pouvoir m’y référer plus facilement, à l’oral, au besoin.

Une autre carte, destinée à rappeler les différentes postures à adopter face à l’information est, elle, affichée en classe

Carte méthodologique : analyse de l’information pour les élèves par Julien Machet (affiche)

Ces deux cartes sont à télécharger en version modifiable (ppt) ou pdf.

De la même manière, deux autres affiches sont présentes dans la classe : le curseur de vraisemblance (visible au centre de la carte) et l’échelle de la preuve en sciences.  Cette dernière affiche est très pratique pour aider à prendre l’habitude de distinguer une simple opinion d’une connaissance construite. De plus, par exemple, lors d’une démarche expérimentale si l’élève énonce une hypothèse ou une conclusion il peut dans les deux cas se positionner de façon argumentée sur le curseur de vraisemblance. L’expérimentation méthodique permet d’apporter (potentiellement) pour la conclusion une preuve plus solide que la simple opinion de départ.
Cette carte, comme la précédente, n’a pas la prétention de présenter une liste exhaustive. Il serait sûrement intéressant qu’elle soit déclinée à ce niveau de simplification (au minimum) dans toutes les matières.
Ce qui m’intéresse en produisant cette carte pour les élèves est d’essayer ainsi :

  1. de montrer que les savoirs, savoir-faire et savoir-être (en collectif) sont utiles voire absolument nécessaires pour trier correctement les informations ;
  2. de développer ainsi des attitudes, des savoir-faire et quelques savoirs propres à l’esprit critique ;
  3. de rendre explicite la méthodologie de la construction de connaissance en science dans l’enseignement des contenus habituels et surtout de justifier l’exigence d’honnêteté intrinsèque à cette méthodologie ;
  4. de tenter de faire toucher du doigt la montagne de travail rigoureux qui a été abattue avant nous et qui nous permet d’avoir toute cette connaissance à disposition. Et de les inciter à savoir également faire confiance de façon raisonnable et justifiée dans les connaissances enseignées.

Je développerai la manière d’intégrer ces différents axes d’analyses dans mes cours dans un prochain article.
Ces cartes et ces réflexions sont amenées à être modifiées et améliorées. N’hésitez pas à me contacter à ce sujet.

Julien Machet : julien_machet@hotmail.com

Croyances, connaissances et boule de neige

Quand nous abordons dans nos cours la question de la distinction entre croyances et savoirs (ou connaissances, je ne ferai pas la distinction ici), cette distinction repose sur un postulatqui pose bien des problèmes.Croyances et savoirs sont-ils, en effet, si facile de les distinguer ? L’objet d’une telle discussion anime les épistémologues depuis des lustres et en quelques heures ou lignes, il serait bien entendu illusoire d’apporter une réponse nuancée. Il est par contre possible de faire réfléchir à cette question, et de bien des manières. Nous proposons ici un atelier très simple à mettre en place, décliné sous la forme d’un débat boule de neige et permettant de faire émerger la complexité de cette problématique, donnant ensuite quelques pistes pour y répondre.

Le débat « boule de neige »

Principe du débat

Le débat « boule de neige » est, comme son nom l’indique, un débat permettant « d’accumuler » les contributions de plusieurs élèves/étudiants/personnes sur un sujet donné1. Il se déroule en différentes étapes et l’objectif est de faire participer toutes les personnes, pour échanger des arguments et construire une réponse collective sur un sujet donné. Chaque étape est chronométrée, permettant de rythmer les discussions. Seuls dans un premier temps, les participants se regroupent petit à petit en différentes « boules » pour échanger leurs arguments et discuter.

Déroulement du débat

Pour commencer, il faut tout d’abord choisir une affirmation, une phrase sur laquelle on souhaite faire réfléchir.

  • On commence le débat boule de neige par une phase de réflexion individuelle avec la consigne suivante : « Êtes-vous d’accord ou pas avec cette affirmation ? » puis « Trouver des raisons/arguments justifiant votre position. » Cette première étape peut durer entre une et trois minutes afin de laisser le temps à chacun de prendre conscience du problème posé par l’affirmation.
  • Dans une deuxième étape, on regroupe les participants deux par deux, toujours avec les même consignes auxquelles on ajoute qu’il faut maintenant présenter ses arguments et cerner les points d’accord et de désaccord. Cette phase peut durer entre deux et cinq minutes maximum : en effet, à deux, il arrive souvent que les arguments échangés ne soient pas très nombreux. Mieux vaut alors enchaîner sur l’étape suivante.
  • La troisième étape permet de regrouper par quatre les participants (on réunit les groupes précédents deux par deux). Les consignes sont identiques. C’est sans doute l’étape la plus prolifique et pertinente du débat, aussi prévoir entre 10 et 15 minutes est tout à fait raisonnable.
  • On réunit ensuite les « boules » de quatre pour former des groupes de huit, toujours avec les mêmes consignes, précédées de cette recommandation : « désignez une personne de chaque groupe pour résumer en quelques phrases les différents arguments avancés précédemment ». À huit, la discussion est souvent animée, mais on remarque aussi que certains peuvent prendre plus (trop) souvent la parole : l’occasion de rappeler quelques règles utiles comme le bâton de parole (avec restrictions sur le nombre de fois autorisées) ou la désignation d’un responsable donnant la parole au fur et à mesure des demandes (mains levées).
  • Selon la disposition de la salle et l’envie ou pas de l’animateur-trice, on peut former des groupes de seize. Mêmes consignes.
  • La dernière étape consiste à réunir tous les participants : debout, en cercle, tout le monde débat ensemble. Si un consensus se dégage, on peut demander de l’indiquer. Dans le cas contraire, on demande de rapporter les différents points de divergences.

  • Le rôle de l’animateur-trice dans toutes ces étapes est de gérer le temps et, dans la dernière étape, de s’occuper de la prise de parole du groupe (ou de désigner quelqu’un pour le faire). Pendant toute la durée des débats, il-elle circulera autour de chaque groupe, aidant ou relançant si nécessaire les participants à nuancer, envisager d’autres pistes, sans répondre directement aux questions portant sur le fond du sujet. Il est important de garder un certain retrait vis-à-vis des échanges de chaque groupe afin d’éviter au maximum le regard du « sachant » à un moment où chacun est invité à exprimer son point de vue de manière totalement égale aux autres.

Croyances ? Connaissances ?

Le choix de l’affirmation

Pour faire réfléchir et discuter élèves, étudiants ou enseignants en formation, j’ai toujours choisi la même affirmation : « Les croyances s’opposent aux connaissances« . Elle permet de faire émerger un ensemble de questions et de problèmes que les participants, ensemble, vont tenter de résoudre. Par le jeu des échanges, les personnes les plus convaincues dès le début se rendent compte que d’autres avis peuvent être légitimes, en fonction de la force des arguments avancés. Certains m’ont parfois suggéré d’inverser le sens de l’affirmation, ce que j’ai fait, sans observer de grands changements dans les débats entendus.

Points de vigilance

Le rôle de l’animateur du débat est crucial : il faut être capable de laisser débattre les participants sans intervenir comme signalé ci-dessus, mais il est aussi nécessaire de savoir relancer les échanges quand ceux-ci sont au point mort. On pourra par exemple poser des questions au groupe comme « Êtes-vous d’accord sur le sens du mot croyance ? » ou « D’après vous, quels types de croyances s’opposent aux connaissances ? ». On pourra également demander de bien penser à justifier chaque point de vue donné, ou encore de faire la liste des points d’accord ou de désaccord entre les participants.

On peut également conseiller, avant chaque nouvelle « boule », que chaque groupe distinct résume la teneur de ses échanges précédents, permettant ainsi de ne pas tout répéter et d’avancer dans le débat.

Quand arrive le regroupement à plus de 8, se pose la question de la parole. Après quelques minutes passées à débattre, je demande à chaque groupe s’il est satisfait de la manière dont se passent les échanges. Il se peut que laisser la gestion de la parole sans règle explicite fonctionne bien, mais on peut aussi donner quelques conseils comme utiliser un bâton de parole (ne parle que celle ou celui qui a le bâton ou quelque autre objet), ou désigner une personne responsable d’indiquer à qui vient le tour de parler.

Enfin, la dernière « boule » – le groupe entier donc – se réunit pour la dernière partie du débat. Il est alors utile de rappeler que l’objectif de ce dernier regroupement est de parvenir à exprimer de manière collective les différents avis qui ont émergés, avec leurs justifications, leurs arguments ou toutes raisons amenant à considérer qu’une opinion mérite d’être entendue.

Ce type de débat peut aussi être utilisé pour prendre une décision collective : la dernière étape étant utilisée pour faire émerger les différentes propositions et choisir parmi elles le cas échéant.

Quant à la manière d’utiliser ce débat pour traiter de la question de fond sur la différence entre croyances et connaissances, ce sera l’objet d’un prochain article.

Scepticothèque : films et esprit critique

Voilà plusieurs mois que Vivien Soldé, doctorant en sociologie à l’Université de Reims Champagne-Ardenne, nous a parlé de sa « scepticothèque : la cinémathèque sceptique et zététique » regroupant des œuvres cinématographiques en lien avec l’esprit critique, le scepticisme, l’autodéfense intellectuelle. C’est un travail précieux que nous partageons aujourd’hui car il regroupe et permet de (re)découvrir des films parfois anciens, mais dont l’objet interroge des thématiques que nous avons l’habitude de rencontrer dans notre vie de sceptiques… Du Procès du singe en passant par Contact, Yéti et compagnie, ou encore Experimenter, l’ensemble de ces œuvres peut aussi constituer un vivier pertinent de ressources pédagogiques, à exploiter avec élèves et étudiants, pour travailler sur les thématiques abordées.
Cerise sur le gâteau, Vivien a également concocté une sélection de 10 films pour le confinement (celui de mars-avril est ici), à déguster entre deux apéros à distance…
Merci et encore bravo à lui pour tout ce travail !

La scepticothèque est à découvrir ici

10 films « sceptiques » pour le confinement (1) à regarder entre deux apéros à distance : c’est là

10 filmes « sceptiques » pour le confinement (2) à regarder entre deux apéros à distance : c’est là

Conférence Esprit critique et sciences ( Lycée Fourcade – D.Caroti) : quelques extraits

Dans le cadre d’une conférence donnée en novembre 2019 au lycée Marie Madeleine Fourcade de Gardanne, notre collègue Denis Caroti avait été filmé… Mais l’enregistrement n’ayant pas les qualités attendues, nous lui avons demandé de publier certains extraits de celle-ci, en mode diaporama commenté, extraits que nous publions à présent. Cette conférence, organisée par Véronique Bianchi pour la « cafèt des sciences », était à destination des élèves et des enseignants et personnels présents. Merci à ces derniers pour leur accueil chaleureux en coulisse ainsi que pour toute l’attention des élèves pendant cette intervention.

Esprit critique ?

Cette première « pastille » présente ce que l’on peut entendre par esprit critique en lien avec l’enquête et l’analyse de l’information : qu’est-ce que l’esprit critique et pourquoi s’en inquiéter ?

Quelques références pour aller plus loin :

Évaluer les preuves

Dans cette vidéo, après avoir défini la notion de preuve, on présente l’échelle des preuves ainsi que les différents sens du mot science, l’importance de préciser les types de registres qui s’entremêlent dans un débat ainsi que les limites et forces de la science en tant que démarche d’enquête et ensemble de connaissances.

Quelques références pour aller plus loin :

Prendre conscience de la limite de nos sens

Dans la vidéo suivante, on aborde la question de la faillibilité de nos sens à travers quelques exemples d’illusions d’optique classiques : l’objectif n’est pas de faire douter systématiquement de nos sens mais plutôt de faire comprendre qu’ils ne sont pas infaillibles : si l’on souhaite gagner en fiabilité, il sera alors utile (et rationnel) d’avoir recours à des preuves plus solides que notre seule expérience personnelle.

Pour aller plus loin :

  • Doit-on encore présenter le délectable cours en ligne de notre collègue et Cortexien de la première heure Richard Monvoisin qui aborde de nombreux exemples sur la limite de nos sens ?

Comment évaluer un témoignage ?

Dans cette partie, il est question d’apprendre à placer son curseur de vraisemblance en fonction du contenu du témoignage que l’on reçoit : toutes choses égales par ailleurs, plus une affirmation sort de l’ordinaire et des connaissances que l’on a, plus on doit exiger des preuves solides soutenant celle-ci. C’est, entre autre, ce que le philosophe David Hume relevait déjà il y a trois siècles dans son Enquête sur l’entendement humain mais aussi Laplace quelques années plus tard en écrivant : « De ce qui précède, nous devons généralement conclure que plus un fait est extraordinaire, plus il a besoin d’être appuyé de fortes preuves ; car, ceux qui l’attestent pouvant ou tromper ou avoir été trompés, ces deux causes sont d’autant plus probables que la réalité du fait l’est moins en elle-même. » (Théorie analytique des probabilités, 2e édition, 1812, p.17)

L’effet cigogne (ou comment ne pas confondre corrélation et causalité)

Dans cette vidéo, on aborde la fameuse confusion corrélation-causalité, que notre collègue Henri Broch a nommé « Effet cigogne » il y a déjà plusieurs années : un lien statistique entre deux variables (corrélation) n’implique pas forcément un lien de causalité entre celles-ci… Attention, la conclusion sur l’établissement du lien causal n’est pas l’objet de cette vidéo : pour en savoir davantage, voir les références ci-dessous.

Pour aller plus loin :

Effet paillasson et impostures intellectuelles

Dans cette dernière vidéo, on présente ce qu’a nommé Henri Broch « l’effet paillasson » ainsi que les dérives qui y sont liées, notamment en termes d’impostures intellectuelles dans le champ du soin (avec le recours au verbiage pseudoscientifique).

Pour aller plus loin :

Activités Esprit critique et sciences au lycée et collège

Florian Stocker est professeur de Sciences de la Vie et de la Terre (SVT) dans l’académie de Grenoble. Il fait partie de ces collègues que nous avons eu la chance de rencontrer lors de nos formations pour enseignants et qui travaillent en toute discrétion (mais en toute efficacité) dans leurs classes pour développer l’esprit critique de leurs élèves à travers les cours de sciences. L’occasion pour nous de partager les activités qu’il a mises en place ces dernières années : des bases de la démarche scientifique en passant par la toxicologie ou la théorie de l’évolution, les cours de SVT sont l’occasion d’incruster des contenus critiques, la preuve s’il en fallait que « faire le programme » et éduquer à l’esprit critique est non seulement possible mais souhaitable. Merci et bravo à lui !

Voici les différentes activités proposées par Florian. Le titre, l’introduction et les objectifs présentent chacune d’entre elles. Des liens permettent de récupérer les différents documents utilisés.

Introduction à la démarche scientifique

Cette séance peut être réalisée en enseignement commun de 1ère ou de Terminale, sur un temps de 2h.

L’attribut alt de cette image est vide, son nom de fichier est CorteX_Couteau_suisse_EC_et_sciences-1024x1024.png.

Le programme insiste en effet sur la nécessité de former les élèves à la démarche scientifique et de son rôle fondamental dans la compréhension du monde.
Consacrer une séance entière pour parler sérieusement du concept de science peut être un plus.

Objectifs

Cette activité a pour buts :

  • d’apprendre à distinguer opinion, croyance, fait scientifique, science ;

  • de prendre conscience de l’existence de biais cognitifs ;

  • d’apprendre à hiérarchiser les preuves (expérience, étude, témoignage, etc…) ;

  • de comprendre que le travail du scientifique est de lutter contre (ou de valider) des idées préconçues et des préjugés à l’aide d’une démarche rigoureuse.

Documents à télécharger

Description-de-la-séance-Introduction-à-la-démarche-scientifiqueTélécharger

cartes-pour-hierarchisation-des-preuves-empiriques-1Télécharger

Intro-démarche-scientifique-Diapo-1Télécharger

Intro-démarche-scientifique-1Télécharger

Une-députée-LREM-relaie-une-FakeNews-sur-le-prétendu-salut-nazi-dun-Gilet-Jaune-F226111820h-1Télécharger

Les dinosaures ont-ils existé ?

Cette activité peut être réalisée lors du cycle 3 au collège lors de l’étude des classifications des êtres vivants par groupes emboîtés, ou lors du cycle 4 lorsqu’on reparle d’évolution.

L’attribut alt de cette image est vide, son nom de fichier est CorteX_Rasoir_Occam_theorie_extinction_Dinosaure.jpg.

Lorsqu’on enseigne des dans des milieux défavorisés, ces thématiques sont souvent très étrangères aux élèves qui présentent très spontanément une vision « fixiste », qu’elle soit guidée ou non par un milieu culturel spécifique. Très souvent, on se retrouve confronté à des élèves pour qui un dinosaure est plus une marque comme le seraient les Pokémon et autres franchises commerciales…
Comment se débrouiller quand un quart d’une classe vous affirme : « bien sûr que non, les dinosaures n’existent pas ! » ?

Objectifs

Cette activité a pour buts :

  • d’établir pour les élèves l’idée que notre point de vue peut évoluer sur un sujet en fonction des preuves apportées (curseur de vraisemblance…) ;

  • d’amener les élèves à comprendre qu’une posture d’esprit où on ne change jamais d’avis n’est pas rationnelle et peu efficace pour comprendre le monde qui nous entoure ;

  • de confronter les élèves à de vrais fossiles (et de faux éventuellement) ;

  • de déterminer quelles hypothèses sont nécessaires pour admettre l’existence de dinosaures.

Documents à télécharger

Description-de-la-séance-Les-dinosaures-ont-ils-existéTélécharger

Activité-2-ClassificationTélécharger

Activité-2-Classification-GroupesTélécharger

S’informer sur les méthodes de contraception naturelles et sur la pilule contraceptive

Cette activité peut être réalisée lors du cycle 4 au collège.
Elle peut s’inscrire dans les programmes de SVT à la fin de la partie sur le fonctionnement des organes reproducteurs ou après avoir étudié le rôle des hormones dans le contrôle du cycle menstruel.
Elle se divise en deux parties, qui occupent 2h entières :

  • Une première où les élèves travaillent en binômes sur à partir de sites internet

  • Une seconde où on met en commun les informations prélevées sur les sites, puis on établit une conclusion sur les critères de fiabilité de l’information et de présentation de la démarche scientifique
    Cette séance a été mise en place en salle informatique en collaboration avec la documentaliste de notre collège ; nous avons ainsi pu faire coanimation et mieux aider les élèves au travail, ainsi que nous répartir les phases magistrales en fonction de nos compétences respectives : correction et repérage des informations pertinentes sur les sites pour la documentaliste, et conclusion sur la démarche scientifique pour moi-même.
    Il existe deux versions de cette séance, une plutôt orientée pilule (plus simple d’accès) et un plutôt pilule vs méthodes naturelles (plus difficile d’accès).

Objectifs

Cette activité a pour buts :

  • d’apprendre à discerner les informations pertinentes de fond (arguments utilisés, sources…) et de forme (auteur, style, expression, volume…) qui permettent de juger du degré de confiance à accorder à un site internet ;

  • de s’informer des avantages et inconvénients de la pilule contraceptive et de discuter de l’importance ou non des risques liés à son utilisation, ainsi que de son efficacité ;

  • de s’informer sur l’efficacité discutable de méthodes contraceptives dites « naturelles » et de l’importance relative de leurs avantages et inconvénients ;

  • d’amener les élèves à découvrir comment sont produits des arguments à base d’études scientifiques et pourquoi la démarche scientifique reste plus fiable qu’une opinion ou une croyance.

Documents à télécharger

Description-de-la-séance-ContraceptionTélécharger

Diapo-méthode-scientifiqueTélécharger

Diapo-méthode-scientifiqueTélécharger

tab-methodnat-correctionTélécharger

tab-methodnat-eleves-2020Télécharger

tab-pilule-eleves-2020Télécharger

Les centrales nucléaires françaises de la vallée du Rhône sont-elles adaptées au risque sismique ?

Cette activité peut être réalisée lors du cycle 4 au collège.
Elle peut s’inscrire dans les programmes de SVT à la fin de la partie dédiée à la compréhension des notions de risque, d’aléa et de vulnérabilité.
J’indiquerai pour cette séance uniquement les éléments en « plus-value » par rapport à une séance classique, c’est-à-dire ce qui peut être ajouté à la fin de n’importe quelle activité sur ce thème pour compléter et remobiliser les notions abordées sur ce sujet. Entre 30 min et 1h sont nécessaires pour cette activité complémentaire.
On peut également envisager cette séance dans la partie « Choix énergétiques et impacts sur les sociétés » dans le programme d’enseignement scientifique de Terminale (plutôt en Physique-chimie), lorsqu’il est demandé de discuter des avantages et inconvénients de choix énergétiques comme le nucléaire.
Voici les liens vers les différents articles utilisés pour le cas où vous souhaiteriez les utiliser en entier :
https://france3-regions.francetvinfo.fr/auvergne-rhone-alpes/drome/seisme-du-11-novembre-centrale-nucleaire-du-tricastin-drome-presente-t-elle-danger-1755921.html
https://www.leparisien.fr/societe/seisme-dans-la-drome-la-centrale-nucleaire-de-cruas-arretee-pour-un-audit-11-11-2019-8191077.php
https://www.liberation.fr/checknews/2019/11/12/apres-le-seisme-en-ardeche-doit-on-s-inquieter-de-l-etat-des-centrales-nucleaires-de-cruas-et-tricas_1762771

Objectifs

Cette activité a pour buts :

  • d’étudier le traitement d’un séisme par différents médias, et de s’intéresser aux raccourcis qui peuvent être utilisés ;

  • de s’intéresser aux différents acteurs qui participent aux débats sur le nucléaire (associations, ONG, entreprises, organismes indépendants financés par l’état …) et leurs points de vue ;

  • de comprendre comment est construite une norme sismique, par qui… ;

  • de s’approprier mieux les échelles de magnitudes (puissance) de séismes, et souligner leur caractère logarithmique.

Documents à télécharger

Description-de-la-séance-Risques-sismiques-et-nucléairesTélécharger

Activité-Risques-sismiques-DiapoTélécharger

Les pollutions médicamenteuses de l’eau – Introduction à la toxicologie

Cette activité prend place au cycle 4 au collège en SVT. Elle peut s’intégrer dans plusieurs parties du programme, avec notamment la gestion d’une ressource (l’eau), ou encore les interactions entre activité humaine et la préservation des écosystèmes.
Elle nécessite d’avoir préalablement abordé les notions du fonctionnement de la reproduction chez l’homme, et le rôle du contrôle hormonal dans la biologie reproductive. En physique-chimie, il est nécessaire de s’assurer que les élèves sont familiers avec les notions de concentration ; dans le cas contraire, il faut impérativement prévoir des exercices simples d’introduction à cette notion. Il est également nécessaire de s’entraîner à convertir les différentes unités, notamment celles peu utilisées (μg, ng…).
Il peut être intéressant de commencer la séance en distinguant pollution « chimique » et pollution biologique de l’eau, cette dernière causant bien plus de morts : c’est la cinquième cause de mortalité dans le monde (autour de 2 à 3 millions par diarrhées). Les pollutions toxiques ou cancérigènes sont bien moins nombreuses notamment car elles tuent au bout de nombreuses années et pas à coup sûr. Mais finalement, il s’agit d’une question de dose.

Objectifs

Cette activité a pour buts :

  • de comprendre les bases de la toxicologie, et notamment la notion de dose ; ainsi, un produit peut être présent mais si sa teneur est trop faible il peut ne pas causer de problèmes ;

  • de comprendre la notion de perturbateur endocrinien et le danger qu’ils représentent pour l’environnement voire l’homme par une action à très faible dose ;

  • d’alerter sur les risques encourus par les écosystèmes par la pollution, souvent oubliés par la préoccupation en termes de santé humaine ;

  • de comprendre la nécessité de surveiller la teneur en hormones de synthèse des cours d’eau et de l’eau potable ;

  • de comprendre que les stations d’épuration jouent souvent un rôle d’élimination des polluants chimiques ;

  • de discuter la qualité de l’eau dans les pays dits « développés » et les pays plus pauvres où la qualité de l’eau est bien plus discutable ;

  • de se rassurer quant à la consommation d’eau ou d’aliments pollués par chez nous : de nombreux articles alarmistes détectent des traces de produits dans l’eau ou les aliments, mais c’est la dose qui fait le poison ;

  • de présenter des données issues d’études scientifiques ; comprendre le principe d’une méta-analyse ;

  • de s’entraîner à manipuler les unités et les conversions.

Documents à télécharger

Description-de-la-séance-Pollutions-Intro-toxicologieTélécharger

Activité-3-Perturbations-environnementalesTélécharger

La théorie de l’évolution est-elle valide ?

Cette activité prend place en classe de 2nde générale et technologique.
Elle peut s’inscrire dans les programmes de SVT à la fin de la partie dédiée aux forces évolutives influençant la biodiversité : pour la mener correctement, il est donc nécessaire que les élèves aient déjà étudié les notions de mutation, de dérive génétique et de sélection naturelle.
Elle dure deux séances de 1h30.

Objectifs

Cette activité a pour buts :

  • de définir ce qu’est une théorie scientifique et de distinguer l’usage courant du mot théorie de l’application de ce terme au domaine scientifique ;

  • de comprendre les caractéristiques qui permettent d’estimer la solidité d’une théorie scientifique ; apprendre à distinguer ce qui peut ou non être remis en cause par de nouvelles découvertes et comment évolue une théorie scientifique ;

  • de consolider la compréhension de la théorie de l’évolution et revoir les forces évolutives ;

  • d’identifier qui cherche à rejeter cette théorie et comprendre que leur démarche n’est pas scientifique ;

  • de critiquer quelques arguments créationnistes.

Documents à télécharger

Description-de-la-séance-Théorie-de-lévolutionTélécharger

Diapo-Théorie-évolutionTélécharger

TP-8-bis-TableauTélécharger

TP-8-bisTélécharger

À propos du critère de réfutabilité et des hypothèses ad hoc

et

Le critère de réfutabilité est bien connu dans le milieu zététique : élément clé permettant de distinguer sciences et pseudosciences, il est pourtant plus difficile à manier qu’il n’y paraît. Afin d’éviter que le corps astral de Karl Popper ne se retourne dans son plan cosmique sépulcral, notre collègue Jérémy Attard nous aide à nous y retrouver, rappelant les bases de ce concept majeur d’épistémologie, puis en pointant les écueils à contourner lorsqu’il est question de le vulgariser.

Simplifier, sans déformer

Dans notre enseignement de la zététique nous avons souvent coutume de déclarer : « Une proposition irréfutable n’est pas scientifique ! » ce qui pourrait sous-entendre qu’une telle proposition ne mérite pas notre attention. Nous entendons par « proposition irréfutable » indistinctement les propositions du type « demain il va pleuvoir ou bien il ne va pas pleuvoir » comme celles du genre « oui, certes, on a des photos de la Terre vue de l’espace, mais c’est des montages de la NASA pour nous cacher que la Terre est plate ! » Le premier cas correspond à une proposition vraie indépendamment de l’expérience et donc qui n’a pas beaucoup de chance de nous apporter une quelconque information substantielle sur le monde ; le second est un cas bien connu d’immunisation contre la réfutation consistant à rajouter une hypothèse ad hoc pour sauver une thèse à laquelle on tient. Lorsque nous parlons de ce critère de réfutabilité, nous faisons évidemment référence à l’éminent philosophe des sciences Karl Popper qui l’a établi et popularisé dans les années 1930 [1]. Cependant, de même qu’il ne viendrait à l’idée de personne, a priori, de présenter l’effet placebo tel que décrit dans la première méta-analyse de Henry Beecher en 1955 sans tenir compte des travaux plus récents qui le remettent assez profondément en question, il nous semble étrange de résumer l’épistémologie, et notamment la réfutabilité, à Karl Popper sans prendre en compte ce qu’il s’est passé après lui. Il ne s’agit pas, dans un enseignement de zététique consacré aux bases épistémologiques, de faire un cours à proprement parler d’épistémologie, bien entendu. Il s’agit simplement de glisser quelques nuances, qui apporteront un peu de profondeur au problème sans pour autant nous perdre dans des considérations stratosphérico-métaphysiques désincarnées des besoins d’outils pratiques de celles et ceux venu-e-s nous écouter.

Photo et citation de Karl Popper

Il s’agit, d’abord, de réaliser une meilleure vulgarisation que celle que nous faisons. Dans toute démarche de vulgarisation, il y a un équilibre subtil à trouver entre la simplicité du propos, dans un but pédagogique de transmission, et sa solidité scientifique. Ce que l’on gagne en simplicité, on le perd très souvent en rigueur et inversement. Ce que nous proposons ici est une façon de présenter le critère de réfutabilité qui améliore cet équilibre par rapport à la façon dont il est habituellement enseigné. N’oublions pas que comprendre le critère de réfutabilité est un objectif pédagogique avant tout : donner un outil simple d’utilisation pour identifier rapidement, au moins dans un premier temps, ce qui distingue une science d’une pseudoscience. Mais une trop grande simplification, pour toute pédagogique qu’elle soit, peut se retourner contre son but initial si l’on ne transmet pas en même temps l’idée que « c’est un peu plus compliqué que ça » ainsi que des pistes pour aller chercher plus loin.

En effet, si l’on creuse un peu l’histoire des sciences d’une part, et la philosophie des sciences d’autre part, on se rend rapidement compte de deux choses : 1/ les théories les plus scientifiques sont fondées sur des propositions irréfutables ; 2/ le fait d’ajouter des hypothèses pour « sauver » une théorie constitue la majeure partie du travail des scientifiques. Une fois ces deux faits établis, et donc mis à jour le caractère un peu « léger » de notre critique usuelle de l’irréfutabilité, nous verrons comment l’améliorer sans trop d’efforts et ainsi ne plus tendre l’homme de paille1 pour nous faire battre. En effet, une personne défendant un contenu pseudoscientifique et un tant soit peu au fait de l’histoire ou de la philosophie des sciences pourrait nous rétorquer que la science, telle qu’on la présente, fonctionne en réalité de la même manière (et elle n’aurait pas tort…) C’est aussi l’occasion de donner quelques références supplémentaires en épistémologie si l’on veut aller creuser le sujet.

La théorie peut-elle réfuter l’expérience ?

C’est un fait bien accepté qu’une théorie scientifique doit pouvoir rentrer en contradiction avec l’expérience. Le raisonnement est relativement simple : une théorie scientifique prétend dire quelque chose de non trivial sur le monde, et donc tirer sa validité de l’expérience. Si une théorie est irréfutable, c’est-à-dire si elle ne produit que des énoncés tautologiques, vrais en dehors de toute expérience, sa validité ne va pas être conditionnée par celle-ci. L’expérience est pourtant in fine la seule manière que l’on a de rentrer en contact avec la réalité objective dont on prétend pouvoir obtenir une information fiable. Une théorie qui ne produit que des énoncés tautologiques ou qui est immunisée d’une manière ou d’une autre contre la réfutation ne pourra donc pas obtenir d’information non triviale sur le monde, et ainsi ne pourra pas être considérée comme scientifique. En d’autres termes, ce qui est intéressant lorsque l’on prétend dire quelque chose sur le monde, ce n’est pas simplement d’avoir raison, mais d’avoir raison alors qu’on aurait très bien pu avoir tort : c’est de ce type de validation qu’une théorie tire sa valeur scientifique.

Il faut donc que la théorie ait une possibilité de rentrer en contradiction avec l’expérience. Mais, plus précisément, qu’est-ce qui rentre en contact avec l’expérience, dans une théorie ? Prenons un exemple concret, tiré de la physique : le principe de conservation de l’énergie. Dans le cadre de la physique newtonienne, celui-ci s’énonce de la manière suivante : « L’énergie totale d’un système isolé se conserve », un système isolé étant défini comme un système qui n’échange ni énergie ni matière avec l’extérieur. En gros, l’énergie peut changer de forme au sein du système mais ne peut pas disparaître ou apparaître si le système est isolé. Posons-nous alors la question : est-ce que ce principe est réfutable par l’expérience ? On a envie de dire oui, à première vue : si l’on observe un système qu’on a de bonnes raisons de considérer comme isolé et dont l’énergie totale augmente ou diminue, alors on pourrait dire que l’on a réfuté ce principe. Pourtant, penser de cette façon est une erreur à la fois au regard de l’histoire que de la philosophie des sciences. En effet, historiquement, à chaque fois que ce principe a été remis en question, on ne l’a jamais abandonné : on l’a au contraire considéré comme vrai a priori, ce qui a poussé les physicien-ne-s à inventer de nouvelles entités ou des nouveaux phénomènes (par exemple, des formes d’énergies ou des particules inconnues jusqu’alors) pour « sauver » ce principe contre l’expérience : la théorie peut en quelque chose parfois réfuter l’expérience2.

Et cette méthode a très souvent porté ses fruits puisqu’elle a conduit à la découverte de Neptune, des forces de frottements, des neutrinos ou encore du boson de Higgs : dans chacun de ces cas précis, face à une réfutation par l’expérience, on a imaginé des hypothèses pour expliquer pourquoi l’expérience ne collait pas avec ce que l’on avait prédit, tout simplement parce que la solidité de la théorie était posée comme une certitude acquise au vu de ses nombreux succès expérimentaux précédents. On trouvera de nombreux exemples de cette façon de fonctionner en particulier dans les travaux de Thomas Kuhn. Celui-ci, dans son ouvrage majeur [2], décrit en effet l’activité « normale » du ou de la scientifique comme étant la résolution de problèmes au sein d’un paradigme donné. Les « problèmes » dont il s’agit ne sont donc absolument pas considérés, de ce point de vue, comme des réfutations de la théorie dans son ensemble, mais simplement comme des anomalies qu’une reconfiguration de la théorie doit pouvoir absorber. Les anomalies fondamentales, comme celle de l’avancée du périhélie de Mercure, ne sont considérées comme telles que rétrospectivement, et peuvent très bien être parfaitement connues de la communauté scientifique pendant des décennies sans que cela n’implique la remise en question profonde de la théorie sous-jacente.

Du point de vue philosophique, maintenant, cela n’a pas vraiment de sens de considérer qu’un principe fondamental comme celui de la conservation de l’énergie puisse être vrai ou faux : en effet, si face à une contradiction avec l’expérience, on déclare que ce principe est faux, on ne peut plus rien faire ; on n’a pas réglé le problème, on est juste sorti du cadre au sein duquel c’était un problème – ce qui n’est pas du tout la même chose. Par exemple, le problème de l’accélération de l’expansion de l’univers, en cosmologie, est fondamentalement un problème de conservation de l’énergie. Si l’on déclare qu’en fait l’énergie ne se conserve pas, que ce principe est faux, l’accélération de l’expansion n’est plus un problème – son aspect problématique n’existe qu’au sein d’un paradigme où l’énergie se conserve. L’ennui est qu’une fois considéré ce principe comme réfuté, on se retrouve démuni pour faire de nouvelles prédictions, puisque tout ce que l’on avait pour parler de ce pan de la réalité était justement le principe de conservation de l’énergie !

Les programmes de recherche

Ainsi, devant ce double constat, il est intéressant d’affiner ce critère de réfutabilité et d’emprunter à Imre Lakatos, philosophe hongrois et disciple de Karl Popper, la notion de programme de recherche [3]. Pour Lakatos, un programme de recherche est constitué d’une part d’un noyau dur formé de définitions, de principes, de propositions définissant un cadre avec lequel on va investiguer un pan du réel, et d’autre part d’une certaine quantité d’hypothèses auxiliaires desquelles on va déduire, à l’aide des règles du noyau dur, des prédictions qui pourront rentrer en contradiction avec l’expérience. Ce sont ces prédictions-là qui doivent être réfutables, et rien d’autre. Si une prédiction rentre en contradiction avec l’expérience, alors on va modifier des hypothèses auxiliaires afin de résoudre cette contradiction. Un programme de recherche génère alors une suite de théories où l’on passe de l’une à l’autre par un changement d’hypothèses auxiliaires. Le problème, bien sûr, est qu’il y a toujours beaucoup de façons de réajuster notre édifice théorique afin de faire coller une prédiction avec l’expérience3. Karl Popper en est d’ailleurs lui-même bien conscient. Comme l’écrit Lakatos :

« Popper (…) en convient : le problème est de pouvoir distinguer entre des ajustements qui sont scientifiques et d’autres qui sont pseudoscientifiques, entre des modifications rationnelles et des modifications irrationnelles de théorie. Selon Popper, sauver une théorie à l’aide d’hypothèses auxiliaires qui satisfont des conditions bien définies représente un progrès scientifique ; mais sauver une théorie à l’aide d’hypothèses auxiliaires qui n’y satisfont pas représente une dégénérescence. »4

La planète Vulcain : trajectoire calculée mais jamais observée…

Pour le falsificationnisme méthodologique dont se réclame Karl Popper, on a le droit de rajouter ou de modifier certaines hypothèses suite à une contradiction avec l’expérience si cette modification augmente le niveau de réfutabilité de la théorie, c’est-à-dire si cela nous pousse à faire de nouvelles prédictions indépendantes du fait de simplement résoudre la contradiction initiale. Si ces nouvelles prédictions, réfutables, sont validées, alors on a augmenté notre connaissance sur le monde, et c’était une bonne chose de « protéger » notre théorie de la réfutation par l’ajout d’hypothèses. L’exemple de la découverte de Neptune est parlant. Au début du dix-neuvième siècle, la planète du système solaire la plus lointaine alors connue était Uranus, et il s’est vite avéré que sa trajectoire semblait ne pas se soumettre à ce que la théorie de Newton prédisait. Plusieurs solutions s’offraient aux astronomes de l’époque, comme par exemple admettre que la théorie de Newton n’était plus valable à cette échelle. Cependant, la première explication qui fût considérée était qu’il existait une planète encore inconnue à l’époque, dont l’attraction gravitationnelle sur Uranus rendrait compte de sa trajectoire problématique. L’éminent astronome français Le Verrier5 calcula alors les caractéristiques de cette planète (en supposant qu’elle existait) à l’aide des lois de Newton, c’est-à-dire en les considérant comme valides. Neptune fut effectivement observée en 1846 à l’observatoire de Berlin, et ce qui aurait pu être une défaite de la théorie de Newton finit en réalité par en constituer une victoire de plus. Le programme de recherche, selon Lakatos, est alors dans sa phase progressive. Par contre, dès l’instant où la modification d’hypothèses ne permet pas de faire des prédictions réfutables mais simplement de résoudre la contradiction sans augmenter notre niveau de connaissance sur le monde, on se trouve alors dans une phase dégénérative, et la nécessité d’un nouveau programme de recherche, reposant sur un noyau dur différent, se fait sentir. La difficulté est évidemment qu’au pied du mur, on ne peut jamais savoir avec certitude si l’on est dans un cas où l’on peut encore modifier des hypothèses auxiliaires et augmenter notre connaissance ou bien si l’on est face à une aporie intrinsèque du programme de recherche. Ce n’est que rétrospectivement que la situation s’éclaircit. Dans la continuité de la découverte de Neptune, les astronomes de l’époque avaient aussi conjecturé l’existence d’une autre planète hypothétique, Vulcain, censée se trouvait entre le Soleil et Mercure et expliquait une anomalie, tout aussi bien connue, dans la trajectoire de cette dernière. Pour autant, cette planète ne sera jamais observée6. Il faudra attendre 1915 et la théorie de la relativité générale d’Einstein pour comprendre le mouvement apparemment inexplicable (dans le paradigme newtonien) de Mercure.

Willard Quine [4] parle aussi de ce phénomène – en allant toutefois encore plus loin dans sa critique. Il soutient la thèse du holisme de la confirmation, aussi connue sous le nom de thèse de Duhem-Quine : une proposition particulière ne fait pas face « toute seule » au tribunal de l’expérience, mais c’est l’ensemble de la théorie à laquelle elle appartient et in fine l’ensemble de notre savoir qui est testé lorsque l’on fait une expérience particulière. L’ensemble de notre savoir est un système conceptuel où il existe des connections fortes entre les différents domaines de recherche qui pourrait être pensés a priori comme indépendants. Il traduit donc autrement le fait déjà énoncé qu’il y a toujours plusieurs manières de modifier la toile d’araignée de nos connaissances pour ajuster une prédiction à l’expérience. Il énonce alors un principe de parcimonie : il est rationnel, parmi tous les ajustements possibles, de choisir en premier lieu celui qui modifie le moins de choses dans le reste de nos connaissances. Cela rejoint la métaphore de la grille de mots croisés de Susan Haack [5]. L’état d’ébriété d’un expérimentateur en neurosciences utilisant une IRM ou la fausseté de ses hypothèses seront toujours des explications plus parcimonieuses, face à une contradiction avec l’expérience, que la remise en question des lois de la mécanique quantique régissant le phénomène de résonance magnétique nucléaire sous-jacent au fonctionnement d’un dispositif d’IRM.

Irréfutabilité et méthode

Cette façon de voir les choses, pas beaucoup plus compliquée que la simple présentation du critère de réfutabilité, permet de résoudre le double problème rencontré plus haut. Les principes de bases d’une théorie sont ses règles de grammaire ; cela n’a aucun sens, ni logique, ni pratique, de penser qu’ils puissent être réfutés à l’intérieur de cette même théorie. Pour reprendre ce que dit Lakatos, cité plus haut, ce n’est pas tant une théorie qui est scientifique ou pseudoscientifique, mais plutôt la méthode avec laquelle on va la reconfigurer pour faire face à une réfutation. Plus précisément, face à une réfutation, on va modifier des hypothèses auxiliaires pour faire coller la théorie à l’expérience. La différence entre des astronomes découvrant Neptune et des platistes est alors double : 1/ face à une observation contradictoire, les astronomes « sauvent » une théorie qui est extrêmement bien corroborée par ailleurs, ce qui n’est pas le cas des platistes ; 2/ la reconfiguration de la théorie, dans le premier cas, satisfait à une exigence épistémologique contraignante de parcimonie et de prédictibilité, ce qui n’est pas le cas pour les platistes.

Comme on l’a dit, il reste indispensable, en zététique, de mettre en garde contre les propositions irréfutables en général. C’est un premier pas nécessaire, notamment pour mettre le doigt sur le fait que le propre de la science n’est pas de confirmer à tout prix ses prédictions mais d’échouer à les mettre en défaut – ce qui est impossible, ou trivial, plutôt, si l’on n’a affaire qu’à des propositions irréfutables. Pour autant, il ne semble pas non plus très coûteux de nuancer un peu ce propos, et de reconnaître que dire simplement d’une proposition isolée qu’elle est irréfutable et donc qu’elle n’est pas scientifique est un peu léger comme critique.

Lorsque la proposition en question est un principe de la théorie, sa valeur épistémique ne se juge pas par son aspect réfutable mais à l’aune de son potentiel heuristique, c’est-à-dire de sa capacité à nous faire découvrir de nouvelles entités ou des nouveaux phénomènes. Par exemple, le fait que le principe de refoulement au sein de la théorie psychanalytique soit irréfutable n’est pas un problème en soi ; le problème épistémologique de ce corpus théorique est que ses principes ne mènent à aucune prédiction validée qui aurait pu être réfutée.

S’il s’agit au contraire d’une prédiction dont la réfutation pourrait être résolue par l’ajout d’une hypothèse auxiliaire, la critique ne tient pas non plus : ce n’est pas le fait de sauver une proposition ou un noyau dur tout entier par l’ajout d’hypothèses qui est critiquable, c’est la manière avec laquelle cela est fait. Ainsi, face à toutes les observations terrestres et astronomiques que nous pouvons réaliser, on peut toujours les ajuster pour nous persuader que la Terre est plate. Cet ajustement, comme la plupart, est logiquement possible ; le problème est qu’il ne permet de faire aucune nouvelle prédiction, qu’il est hautement coûteux en hypothèses et qu’il ne tient pas face au modèle concurrent et éminemment plus parcimonieux de la Terre sphérique.

Les outils d’autodéfense intellectuelle issus de cette réflexion sont les mêmes qu’ailleurs : dans l’élaboration d’une connaissance synthétique et objective sur le monde, prédictibilité et parcimonie sont deux maîtres mots pour mener à bien cet art difficile.

Références

[1] K. Popper, La logique des découvertes scientifiques, Payot, 1973 (1934).

[2] T. Kuhn, La structure des révolutions scientifiques, Flammarion, 1972 (1962).

[3] I. Lakatos, A methodology of research programs, Cambridge, 1978.

[4] W.V. Quine, Les deux dogmes de l’empirisme, Harper, 1953

[5] Susan Haack, Le bras long du sens commun : en guise de théorie de la méthode scientifique, Philosophiques, vol. 30 , n°2, 2003, p. 295-320.

[6] W. V. Quine, On empirically equivalent Systems of the World, Erkenntnis, 3, 13–328, 1975.

Esprit critique : outils et méthode pour le 2nd degré

Depuis le lancement du Cortecs en 2010, on rêvait de voir naître un livre consacré à l’esprit critique et s’adressant à tous les enseignants et personnels du collège et lycée, toutes disciplines confondues. Édité par Canopé et paru en mai 2019, on peut dire que c’est fait ! Codirigé par Gérald Attali (inspecteur d’histoire et géographie), Abdennour Bidar (Inspecteur Général de L’Éducation Nationale en philosophie, Denis Caroti (enseignant, formateur et chercheur doctorant), et Rodrigue Coutouly (personnel de direction et à l’époque Proviseur Vie Scolaire), cet ouvrage est le fruit d’un immense travail collectif, bâti entre autre par de nombreux enseignants ayant déjà contribué aux ressources du Cortecs : Vanessa August, Anne André, Marie-Hélène Hilaire, Marion Margerit, Julien Machet, Delphine Laugier, Aline Chirouze, Marie-Laurence Tinet, Guillemette Reviron et bien d’autres dont Pierre Leveau, Hélène Audard, Céline Persini et Stéphanie Bejian qui ont apporté tout leur savoir-faire pour le travail d’édition. Puisse cet ouvrage être un outil utile au service de toute personne, enseignant ou pas, désirant conduire des activités en lien avec l’éducation à l’esprit critique !

Résumé tiré de la page : http://www.pedagogie.ac-aix-marseille.fr/jcms/c_10719993/fr/ouvrage-canope-esprit-critique-outils-et-methodes

Fruit d’un travail collectif mené depuis 2016 entre Canopé et le rectorat d’Aix-Marseille, le livre « Esprit critique : outils et méthodes » publié en mai 2019 dans la collection Agir est un concentré de séquences pédagogiques pour toutes les disciplines. Plus d’une vingtaine d’auteurs ont participé à l’élaboration du contenu, basé sur des expériences de terrain et mises en œuvre au collège et au lycée. L’introduction et la première partie reviennent sur des considérations plus générales, cadres didactique et philosophique ainsi que sur le lien avec les programmes de l’enseignement secondaire. Un chapitre est entièrement consacré aux projets d’établissements.

C’est du sommaire de cet
ouvrage, et par souci de cohérence et de continuité, que les catégories
de présente dans la partie Pédagogie ont été créées. Nous ne manquerons
pas de publier les dernières actualités en lien avec les productions du
site Canopé – Développer l’esprit critique.

Voici la description qu’en donne l’éditeur :

Comment développer
l’esprit critique des élèves et l’exercer avec eux dans le cadre des
programmes du second degré ? Cet ouvrage propose, à travers plus d’une
vingtaine de séquences, des outils et des méthodes éprouvés,
transférables à différents niveaux et contextes, autour de trois
compétences principales : 

  • questionner et mettre à l’épreuve, 
  • analyser et vérifier, 
  • argumenter et débattre. 

Son ambition est de
montrer que l’ensemble des attitudes et habitudes qui constituent
l’esprit critique peut être cultivé quelles que soient les disciplines,
parce qu’il les traverse toutes. Exposant les enjeux et préconisations
liés à cette question, il prend également en compte la dimension
collective de l’esprit critique au sein de l’établissement et de ses
projets citoyens. 


Destiné aux enseignants, ainsi qu’aux équipes éducatives et de
direction des collèges et lycées, il offre des réponses concrètes et des
démarches variées pour faire apparaître les enjeux cognitifs, éthiques,
culturels et civilisationnels de l’esprit critique, à l’échelle de la
classe comme de l’établissement. Cet ouvrage existe en version
numérique.