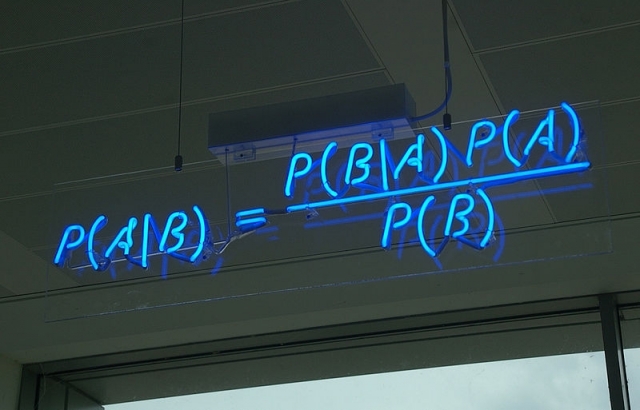
Dans cet article, Florent Tournus nous avait fourni une explication claire et précise de ce que l’on appelle les probabilités inversées. Malgré tout, celles-ci restent difficiles à détecter dans un argumentaire ou une simple déclaration et, même avec de l’entraînement, nous devons souvent fournir un effort intellectuel pour décrypter et analyser les erreurs d’interprétations des probabilités inversées. Avec ces quelques exemples supplémentaires, nous pourrons trouver une aide précieuse en cas de cafouillage cérébral face à ces statistiques et autres probabilités. Aussi, n’hésitez pas et écrivez-nous pour partager vos exemples les plus éclairants.
Exercice – Saurez-vous détecter en quoi nous avons affaire à un effet de probabilités inversées sur cette affiche sortie tout droit d’un restaurant McDonald’s :
Si rien ne paraît suspect à première vue, un petit détour par deux autres exemples s’impose.
Des sous-vêtements dangereux ?
Tout d’abord, voici quelques mots sur les probabilités dites inversées. Comme l’explique très bien Florent dans son article, pour avoir une utilité, une probabilité, exprimée en pourcentage, doit être clairement définie. Si j’affirme par exemple que la probabilité de gagner au loto est de 0,000000052 soit 0.0000052%, je dois alors préciser que ce chiffre correspond à la probabilité de trouver 5 numéros parmi 49 + 1 numéro parmi 10. Même si tout le monde avait compris que l’on ne parlait pas de la chance de trouver seulement trois bons numéros, il est toujours nécessaire de fournir ces précisions : probabilité de quoi ?
Lorsqu’il s’agit d’évaluer le risque de contracter une maladie, en particulier le poids de facteurs environnementaux, les choses se compliquent. Prenons l’exemple d’une maladie comme le cancer des poumons. On peut lire que « le premier facteur de risque est le tabac » avec 81% des décès, en France (voir la page d’accueil du site Fondation Recherche Médicale). Que signifie cette probabilité ? Que 81% des personnes décédées d’un cancer des poumons fumaient du tabac (d’ailleurs rien n’est précisé sur les doses, le type de tabac, etc. mais ce n’est pas le problème qui nous intéresse ici). Autrement dit, la probabilité d’avoir consommé du tabac sachant qu’on est décédé d’un cancer des poumons est de 81%,  et d’en déduire que la cause principale de ces cancers est le tabagisme. Attention, si vous en tirez cette conclusion, vous êtes en train de toucher du doigt le problème des probabilités inversées : ce n’est pas cette statistique seule qui permet d’inférer un lien de cause à effet entre tabagisme et cancer. Car on pourrait très bien trouver, en cherchant un peu, que 99% des personnes décédées portaient des sous-vêtements, sans pour autant en conclure à un lien causal direct entre porter un slip et mourir d’un cancer des poumons. Autrement dit, la probabilité de porter des sous-vêtements sachant que l’on est mort d’un cancer ne nous donne aucune information sur la dangerosité ou le risque de cette pratique.
et d’en déduire que la cause principale de ces cancers est le tabagisme. Attention, si vous en tirez cette conclusion, vous êtes en train de toucher du doigt le problème des probabilités inversées : ce n’est pas cette statistique seule qui permet d’inférer un lien de cause à effet entre tabagisme et cancer. Car on pourrait très bien trouver, en cherchant un peu, que 99% des personnes décédées portaient des sous-vêtements, sans pour autant en conclure à un lien causal direct entre porter un slip et mourir d’un cancer des poumons. Autrement dit, la probabilité de porter des sous-vêtements sachant que l’on est mort d’un cancer ne nous donne aucune information sur la dangerosité ou le risque de cette pratique.
Où se niche l’erreur subtile de raisonnement ? Dans le fait que la probabilité qu’on nous donne n’est pas la probabilité qui nous intéresse, même si elle lui ressemble à s’y méprendre. Ce qui nous intéresse n’est pas la probabilité d’avoir porté une culotte, d’avoir fumé ou de s’être curé le nez sachant qu’un cancer nous a fait passer de vie à trépas. Non, nous voulons savoir l’inverse : la probabilité de mourir d’un cancer sachant qu’on se gratte le nez.
Travailler chez McDo avec « des perspectives d’évolution rapide »
Reprenons le texte de l’affiche. En grand, on peut lire : « Plus de 70% de nos managers et directeurs adjoints ont débuté comme équipiers* ». L’enquête a été réalisée par un institut de sondage (Ipsos 2012, publiée par McDonald’s). Si l’affirmation est vraie, il nous faut nous méfier de la conclusion que nous allons en tirer. Effectivement, il est impossible d’en déduire que de nombreux équipiers deviendront managers un jour, ce que suggère pourtant la phrase « Chez McDonald’s, un emploi permet des perspectives d’évolution rapide. » Traduisons cette phrase dans les mêmes termes que pour l’exemple du cancer : nous savons à présent que la probabilité d’avoir été équipier sachant qu’on est manager est égale à 70% ou plus. Est-ce bien l’information dont nous avons besoin pour connaître les chances d’évolution dans le métier ?
Comme pour les risques sur les maladies, il nous est impossible de conclure à une évolution de poste grâce à cette seule statistique. Souvenons-nous en effet que la probabilité qui nous intéresse est celle donnant les chances d’accéder à un poste de manager sachant que l’on est équipier (et qu’on en fait la demande ou qu’on le désire). Or nous savons simplement l’inverse : la probabilité d’avoir été équipier sachant qu’on est manager, et celle-ci ne sert à rien quant aux possibilités d’évolution de carrière.
Un doute persiste : il se pourrait que cette statistique signifie vraiment quelque chose. Par exemple, que 70% des postes de managers sont réservés à des travailleurs internes à l’entreprise. Ceci est tout à fait exact : on peut devenir manager en étant équipier, la voie n’est pas fermée. Ce qui est fallacieux avec la publicité de cette affiche est de laisser croire à un lien de cause à effet entre ce pourcentage et l’affirmation que « Chez MacDonald’s, un emploi permet des perspectives d’évolution rapide » : l’un n’implique pas l’autre. Avec un calcul rapide à partir des chiffres donnés par MacDonald’s (site officiel, MacDonald’s France) on peut estimer le nombre d’équipiers et de managers. Ce faisant, nous avons trouvé une statistique encore plus intéressante : « 80% des directeurs** ont commencé leur carrière comme équipier ». Utilsons-là pour calculer le ratio directeurs/équipiers. Nous apprenons qu’en moyenne 54 personnes travaillent dans un restaurant, donc 53 ne sont pas directeurs. D’après une de nos sources internes, on peut estimer à 90% la part des équipiers dans le personnel (les cuisiniers sont des équipiers), c’est-à-dire 47 travailleurs environ, nous obtenons un ratio directeurs/équipiers = 1/47 = 0,021 soit 2,1%. Sachant que les managers peuvent être plus d’un par restaurant, le ratio est certainement plus élevé pour ceux-ci. Mais en admettant qu’on atteigne en moyenne le double, cela représente un ratio de 4%. La voie n’est donc pas fermée, mais elle reste très étroite.
Denis Caroti
Note : un autre exemple de probabilités inversées nous est donné par G. Reviron avec les propos d’Eric Zemmour sur la délinquance. De même, on pourra consulter les articles de R.Monvoisin sur le problème du Monty Hall, et de Nima Yeganefar sur la propagande.
———————–
* Impossible de ne pas réagir à ce qualificatif. « Équipier », superbe mot à effet impact et qui enjolive ce qui n’est en réalité qu’un emploi souvent mal payé car à temps-partiel, pour des étudiants précaires qui doivent financer le coût exorbitant de certains cursus et le loyer d’une chambre hors de prix dans une agglomération où l’inflation des loyers oblige à vivre loin de leur faculté, augmentant de fait le temps passé dans les transports. Équipier sonne alors comme la gloire du travail partagé, de l’investissement pour une oeuvre supérieure qui nous dépasse mais pour laquelle nous donnons tout notre possible… Ce sont avant tout des travailleurs sous-payés.
** Les directeurs sont les supérieurs hiérarchiques des managers, il y en a un seul par restaurant, assisté par un directeur adjoint. On pourra consulter l’organigramme sur le site officiel de MacDonald’s.
