
Julien Pinel, enseignant de Physique-chimie au lycée Doisneau (Lyon) et contributeur du CorteX, nous a invité dans sa classe de seconde pour animer un atelier sur les chiffres dans les médias. Je saisis l’occasion pour rappeler que la formation à l’esprit critique fait partie du programme.
J’ai donc monté un atelier qui avait pour objectifs généraux :
– de démontrer qu’il suffit de sélectionner certaines données chiffrées pour « fabriquer » de l’extraordinaire ;
– d’apprendre à questionner les chiffres pour repérer ces petites (ou grandes) manipulations.
Nous racontons ici comment les statistiques de la ligue 1 de football et les performances du buteur B. Gomis, mais aussi la momie Ötzi, les guérisons miraculeuses de Lourdes ou le triangle des Bermudes nous ont permis de faire sentir aux élèves qu’il est parfois nécessaire de confronter les chiffres.
Cet atelier a été repris dans la foulée par un autre enseignant du lycée Doisneau, Ludovic Arnaud. Il raconte son expérience ici.
Nous avons mené cette séance le 12 Janvier 2012 avec deux demi-classes de seconde.
Compétences critiques visées
- placer son curseur de vraisemblance
- questionner les chiffres, les confronter
- savoir repérer les données chiffrées manquantes
Objectifs de la séance
- repérer les chiffres dans un document et les classer selon le critère valeur absolue / valeur relative
- reconstruire une valeur relative à partir de données extraites d’un document
- faire sentir aux élèves que la seule donnée d’une valeur absolue (et même d’une valeur relative) ne permettent pas forcément de construire un savoir
Description de la séance
- Durée
Deux fois la même séance d’1h30, une pour chaque demi-classe - Effectifs
La classe de seconde était scindée en deux groupes de 15 et 16 élèves. - Encadrement
Nous étions deux pour animer l’atelier (Julien Pinel, l’enseignant de physique-chimie de la classe, et moi-même) mais une petite surprise nous attendait : un autre enseignant de physique-chimie et collègue de Julien, un peu curieux de ce qui allait se passer, s’est joint à nous et a laissé traîné ses oreilles. Un observateur discret et inattendu dont nous attendons avec impatience les retours. - Déroulement de la séance
Le groupe de 16 élèves était scindé en 4 groupes de 4 élèves qui travaillaient chacun sur un sujet différent (voir ci-dessous).
Étape 1 – chaque petit groupe visionne son document (le n°1) puis discussion libre en petit groupe
Étape 2 – Chaque élève énonce en moins d’une ligne l’idée développée dans le document puis place son curseur de vraisemblance ;
Chaque groupe explique rapidement aux autres groupes le sujet de son document.
Étape 3 – Les élèves vont chercher les données chiffrées qui viennent étayer l’idée principale ;
Ils placent leur curseur de vraisemblance ;
Chaque groupe donne rapidement aux autres la liste des chiffres recueillis.

Étape 4 – Je lance une discussion collective autour de la question suivante : « Gomis (ou tout autre attaquant de leur club préféré) est-il un bon buteur ? » Pour cela, je demande aux férus de football d’essayer de convaincre les autres du fait que B. Gomis est, selon eux, un bon (ou un mauvais) buteur.
Très rapidement, pour justifier leur point de vue, les élèves évoquent :
- Le nombre de buts marqués par Gomis (en l’occurrence, 7 buts en Ligue 1 au 12 janvier 20011) mais les « non-experts » ne semblent pas convaincus
- Le nombre de buts marqués + nombre de matchs (7 buts sur 19 matchs, ce qui fait à peu près 1 but tous les 3 matchs ) mais même cette valeur relative ne parle pas beaucoup aux « non-experts » : il leur manque un point de comparaison
- Ils en arrivent à dire qu’il leur faudrait pouvoir comparer aux résultats des autres buteurs de Ligue 1 (seuls deux buteurs de Ligue 1 ont marqué plus de buts que Bafetimbi Gomis. Il s’agit d’Olivier Giroud – 13 buts sur 19 matchs – et Kevin Gameiro : 9 buts sur 19 matchs)
Ceci nous a permis de mettre en évidence que, si nous ne sommes pas spécialistes d’un sujet, nous avons besoin de points de repères.
Or nous ne sommes en général spécialistes ni en miracles, ni en disparition d’avions, ni en fraude sociale, ni en taux de mortalité chez les scientifiques…
Étape 5 – Les élèves classent les chiffres recueillis selon les critères valeur absolue / valeur relative
Étape 6 – En groupe, ils essaient de reconstruire, si possible, une valeur relative, éventuellement à l’aide du document n°2 si le n°1 ne le permet pas. Ils placent leur curseur de vraisemblance
Étape 7 (de loin la plus difficile) – En groupe, ils essaient de répondre à la question : quel(s) autre(s) chiffres nous auraient été utiles comme point de comparaison ?
Étape 8 – Julien leur demande, pour le prochain cours, de ramener une valeur absolue et une valeur relative issue du journal télévisé du soir.
Documents utilisés
Nous avions envie de faire travailler les groupes sur des sujets différents pour mettre en évidence le fait que le même processus est très souvent utilisé. Le paranormal est toujours très attractif et a donc motivé mon choix des trois premiers sujets. Julien avait exprimé l’envie de sortir de ce cadre pour montrer que cette manière de faire pouvait aussi être utilisée dans des domaines plus politiques, où la manipulation de l’opinion a des conséquences plus importantes. J’ai donc choisi un document sur la fraude aux prestations sociales.
Il fallait aussi que les documents soient courts, et qu’ils contiennent peu de chiffres pour ne pas noyer les élèves. Voici donc notre récolte :
Poste 1 : Lourdes
Poste 2 : Momie Ötzi
Document 1
{flv}CorteX_TSD_mom1{/flv}
Document 2
{mp4-flv}CorteX_TSD_mom2{/mp4-flv}
Remarque : les données chiffrées récoltées dans les deux documents ne permettent pas de calculer de valeurs relatives. En effet, on nous donne le nombre de victimes depuis 15 ans dans une certaine catégorie de personnes (scientifiques + cameramen + guides de hautes montagnes), le nombre de scientifiques qui sont en contact avec Ötzi aujourd’hui et le nombre de visiteurs du musée en 2007. Ces chiffres ne peuvent être comparés et nous sommes plutôt satisfaits de voir que plusieurs élèves qui ont travaillé sur ce sujet s’en sont rendus compte, même si une petite aide fut nécessaire pour le formaliser.
Poste 3 : Triangle des Bermudes
Document 1
Document 2
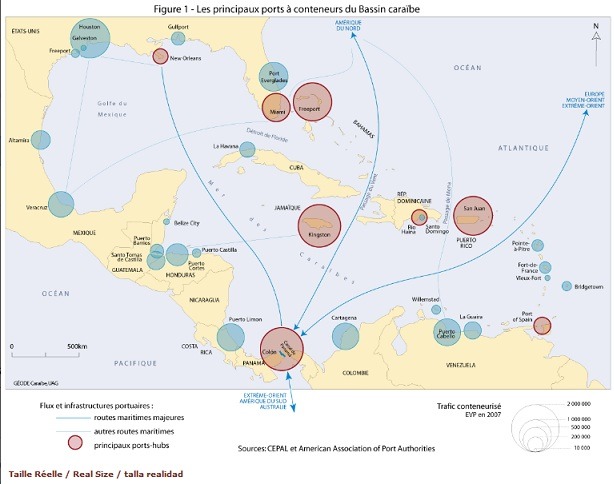
En 2007, on peut supposer qu’un porte-container a une capacité moyenne de 2 300 EVP (source : wikipedia, 10 Janvier 2012 – La flotte mondiale comprenait 3 500 porte-conteneurs au début 20061, pour une capacité totale de 8,1 millions d’EVP).
Avec le deuxième document, les élèves sont censés estimer le nombre de bateaux qui traversent la zone du triangle des Bermudes sur une année. Il a fallu les aider un peu à lire cette carte en leur posant quelques questions préliminaires : que représente cette carte ? Où est le triangle des Bermudes, Que représentent les disques ? Ensuite, ils ont pu seuls donner une première estimation du nombre de bateaux ayant traversé le triangle.
Document 1

Document 2

Document 1 (extrait de l’article)

Document 1 (extrait de l’article)

Remarque : nous avons supprimé le poste 4 pour la deuxième séance car le document était difficile d’accès et moins attrayant que les trois autres. L’article de journal est vraiment long et donner les extraits sans l’article n’a pas beaucoup de sens, puisque cela revient à faire le travail d’extraction des données chiffrées, travail que les élèves sont censés faire eux-mêmes. Pendant la pause, nous avons décidé de supprimer ce poste pour la deuxième séance, en espérant avoir le temps de le traiter collectivement à la fin ; cela nous aurait donné l’occasion de réinvestir les outils vus en petit groupe, mais nous avons été pris par le temps.
Cela reste un bon outil pour un public plus à l’aise avec l’écrit (je l’ai déjà testé sur un format conférence avec des éducateurs spécialisés).
En conséquence, les groupes de travail sont passés à 5 personnes, ce qui a nui à la qualité des échanges. Il faudra trouver un autre document pour les prochaines fois, par exemple un reportage vidéo issu d’un journal télévisé sur la fraude sociale.
Bilan
Dans l’ensemble, tous les groupes ont bien avancé et nous avons pu aborder tous les points. Ceci dit, l’étape 7 est un peu subtile et aurait mérité qu’on s’attarde un plus longtemps dessus mais le temps nous a un peu manqué. Julien nous dira ce que ses élèves en ont pensé et ce qu’ils ont retenu. En attendant, voici le tableau rempli par la deuxième demi-classe – désolée pour la mauvaise qualité de l’image, je l’ai réalisée avec les moyens du bord. Nous n’avions pas pensé à mettre en place cet outil lors de la première séance, c’est dommage, nous aurions pu comparer les deux productions.


Ce que nous modifierons la prochaine fois
1. Dans le souci de ne pas trop guider la réflexion des élèves en anticipant sur certaines questions, je n’avais pas prévu de fiche « papier » pour cadrer la séance, mais plutôt un diaporama qui me permettait de faire défiler les questions au fur et à mesure.
Comme me l’a fait remarqué Julien, cette manière de faire a un gros défaut puisque les élèves ne produisent rien et perdent parfois le fil. Il suggérait donc d’utiliser quand même un support écrit. Après discussion, nous proposons de commencer de la même façon jusqu’à l’étape 4 comprise (c’est l’exemple du football) puis de leur distribuer une fiche qui ressemblerait à ça :
1) Quelle est l’idée principale développée dans votre document (une ligne maximum) ?
2) Indépendamment de votre avis sur la question, les arguments développés dans votre document vous paraissent-ils convaincants ? (5 lignes)
3) Quels sont les chiffres avancés pour argumenter en faveur de cette idée ?
4) Après avoir observé l’exemple de Gomis, remplissez la ligne du tableau qui correspond à votre sujet :
| Valeur(s) absolue(s) | Valeur(s) relative(s) | Quels chiffres auraient été utiles comme point de comparaison ? | |
| Exemple de Gomis | 7 buts | 7 buts sur 19 matchs ≈ 0,37 buts/matchs | Résultats des autres buteurs de la Ligue 1 |
| Momie Ötzi | |||
| Lourdes | |||
| Triangle des Bermudes | |||
| Fraude au RSA |
5) Après ce travail sur les chiffres, que répondriez-vous à quelqu’un qui vous affirmerait, après avoir vu ce document, que Ötzi est une momie maudite ? Ou que Lourdes est une ville miraculeuse ? Ou qu’il y a des disparitions étranges dans le triangle des Bermudes ? (5 lignes maximum)
6) Que retenez-vous de cette séance ? (5 lignes maximum)
Remarque de Julien : il faut garder du temps pour la dernière étape, celle de la conclusion, afin que les élèves s’interrogent eux-mêmes sur ce qu’ils peuvent conclure (ou non) des données présentées dans leur document.
Nous n’avons pas eu le temps non plus de faire en sorte que chaque groupe présente son travail aux autres.
2. Visiblement, les deux demi-classes ont eu le temps de discuter pendant la pause, ce qui est peut-être à l’origine de réactions très différentes du deuxième groupe par rapport au premier (tous les curseurs de vraisemblance étaient à zéro). Il aurait fallu faire en sorte que les groupes ne se croisent pas ou animer les deux séances simultanément.
3. A chaque étape, je souhaitais « mesurer » si les débats avait un impact sur l’avis que se faisaient les élèves sur la thèse présentée dans leur document. Je leur ai donc demandé très régulièrement de positionner leur curseur de vraisemblance. A posteriori ce choix ne nous paraît pas très judicieux : nous nous sommes demandés s’il n’y avait pas un phénomène de conformisme qui empêchait certains élèves de placer ce curseur en fonction de leur ressenti personnel. En effet, même si la consigne précisait qu’il n’y avait pas de bonnes ou de mauvaises réponses, comme les groupes étaient petits, chacun pouvait voir où les autres mettaient leur curseur et pouvait se sentir « bête » d’adhérer à telle ou telle idée. Nous n’avons pas les moyens de mesurer cet effet, mais peut-être pourrait-on essayer de mesurer autre chose que leur propre adhésion en leur demandant si l’argumentaire leur paraît pertinent plutôt que de leur demander s’ils y croient. Une autre piste suggérée par Richard Monvoisin est de contrebalancer la crainte d’être ridicule par une crainte plus grande de perdre. Pour cela, on pourrait leur demander : « seriez-vous prêt à miser 100 euros sur le fait que c’est vrai ? Que c’est faux ? »
Si vous testez ce procédé ou si vous avez essayé autre chose, racontez-nous !
4. Notre présence est un élément perturbateur des discussions dans les groupes. Difficile donc d’évaluer cette séance. C’est d’autant plus frustrant que le collègue de Julien, qui a réussi à se fondre dans le paysage, nous a raconté que leurs échanges étaient passionnants. La prochaine fois, on pourrait tenter d’enregistrer leurs échanges à l’aide de dictaphones laissés sur chaque poste, avec l’accord des élèves, bien entendu.
Logistique
Cet atelier repose sur les moyens informatiques, très souvent à l’origine de déconvenues de dernière minute. Quelques précautions sont toujours bonnes à prendre :
– prévoir d’installer les postes quelques jours avant
– s’assurer que tous les ordinateurs sont équipés de logiciels permettant de lire les documents
– s’assurer que tous les ordinateurs ont du son ou s’équiper de casques si besoin
– vérifier que tous les documents sont lisibles en intégralité,
– avoir de toutes façons tous les documents très rapidement accessibles sur son propre ordinateur, des baffles, un vidéoprojecteur, une rallonge et une multiprise pour pouvoir, en cas de pépin, animer la séance en collectif.
Merci à tous les élèves de 2de 5 du lycée Doisneau qui ont travaillé avec enthousiasme.
Merci également à Julien Pinel et à notre invité surprise qui m’ont donné de nombreuses pistes pour améliorer cet atelier.
Guillemette Reviron
- Pour obtenir ces statistiques, je suis allée, sur les conseils de Denis Caroti, sur le site de l’Equipe.fr, qui recense toutes les statistiques dans l’onglet Ligue 1.