
Nicolas Martin, après avoir étudié les mathématiques appliquées à l’INSA Toulouse, a obtenu son doctorat en automatique au sein du GIPSA-lab et de l’université Grenoble Alpes. Il s’intéresse depuis plusieurs années à la zététique, l’esprit critique et leur transmission auprès du public. Depuis début 2020, Il publie des articles de vulgarisation scientifique et d’esprit critique sur le blog « Mon Œil ! »1Voici une de ses productions:
La zététique est un mouvement de pensée qui promeut l’utilisation de la pensée critique et de la méthode scientifique pour traiter efficacement le tsunami d’informations qui nous parvient chaque jour. Il semble néanmoins que cette démarche serait plus efficace encore si elle était soutenue par une vision bayésienne c’est-à-dire une approche qui prône l’usage des probabilités pour quantifier nos croyances. La démarche zététique est régulièrement le fruit de critiques : elle parait parfois dogmatique, parfois antipathique et parfois inapte à répondre à certains problèmes. Nous verrons dans cet article que le raisonnement bayésien soutient l’approche zététique et lui apporte un peu de nuance. Récemment, plusieurs travaux dans la communauté zététique sont allé dans ce sens, initiés principalement par Lê Nguyen Hoang (influencé par les travaux de Julia Galief écrivaine, conférencière et co-fondatrice du Center for Applied Rationality), avec son livre « La formule du savoir », sa série de vidéos sur le sujet 2 et ses podcasts3, l’approche bayésienne et ses apports à la zététique ont également été traités par Christophe Michel (animateur de la chaine Hygiène mentale)4, Nathan Uyttendaele (animateur de la chaine Chat Sceptique)5 ou encore Thibaud Giraud (animateur de la chaine Monsieur Phi)6. C’est dans ce mouvement que s’inscrit cet article dont l’objectif principal est de montrer comment le bayésianisme corrobore et enrichit certains outils zététiques.
Nous présenterons dans un premier temps quelques points critiques de la zététique qui motivent l’introduction d’un cadre bayésien. Nous introduirons ensuite succinctement le formalisme bayésien avant de présenter dans la dernière partie la contribution principale de cet article : la déduction de deux principes zététiques, rasoir d’Ockham et maxime de Hume, à partir de la formule de Bayes, formule sur laquelle se base l’approche bayésienne.
Cet article est loin de faire le tour de la question. Au contraire, comme son titre l’indique, le but ici est de fournir quelques arguments invitant à une réflexion plus poussée sur l’apport de l’approche bayésienne à la zététique.
Les limites de l’approche zététique
Il semble que l’approche zététique ait une mauvaise image de la part des croyant-e-s et des tenant-e-s des affirmations para-scientifiques7 mais pas seulement, certaines critiques viennent des zététiciens eux-mêmes8. Si certaines critiques peuvent être maladroites, d’autres en revanche nous paraissent pertinentes. Notons également que la plupart des critiques ne concerne pas la zététique dans son essence mais des écueils dans lesquelles il est facile de tomber. Nous proposons une liste de ces critiques ci-dessous. Nous verrons ensuite en quoi le bayésianisme peut répondre en partie à ces défaillances.
Des principes dogmatiques
Le rasoir d’Ockham, la maxime de Hume, la charge de la preuve, la valeur d’une preuve, l’impossibilité de prouver l’inexistence… Ces principes se posent parfois comme des dogmes de la zététique. Ce n’est pas un problème en soi puisque leur justification apparaît a posteriori : On se rend compte, en les utilisant, qu’effectivement on a tendance à se tromper moins souvent. En revanche, justifier a priori que ces principes sont cohérents, sont suffisants et nécessaires est une question plus complexe mais qui soutiendrait d’autant plus la démarche zététique.
En réalité, nous le verrons plus loin: le rasoir d’Ockham et la maxime de Hume peuvent se déduire de la formule de Bayes, formule dont on peut également justifier la cohérence.
De bons outils dans des mains maladroites
Carl Sagan dans The Fine art of Baloney Detection accompagne son texte de cette note appelant à la précaution : Like all tools, the baloney detection kit can be misused, applied out of context, or even employed as a rote alternative to thinking. But applied judiciously, it can make all the difference in the world — not least in evaluating our own arguments before we present them to others9. De même, dans son article critiquant la zététique, Sylvain Poirier fait remarquer : Ce n’est pas parce que beaucoup de principes zététiques affichés sont bons, que tout ce que disent les zététiciens est à croire sur parole. Si la zététique apporte un panel d’outils finement aiguisés, ils peuvent parfois être délétères lorsqu’ils sont utilisés sans un peu d’esprit critique.
Manque d’un formalisme mathématique
Le rasoir d’Ockham nous invite à “Privilégier l’hypothèse la plus parcimonieuse”. Mais comment quantifier la parcimonie d’une hypothèse ? Quelle métrique utiliser ?
La maxime de Hume, elle, stipule que “Une affirmation extraordinaire requiert des preuves extraordinaires”. Mais comment quantifier cette extraordinarité ? Et comment comparer l’extraordinarité d’une affirmation et l’extraordinarité des preuves ?
Bonne nouvelle, même si ces préceptes font office de principes généraux sans prétendre avoir une quelconque valeur quantitative, ils peuvent en fait être déduit de la formule de Bayes. Qui plus est, cette dernière leur donne un sens mathématique.
Manichéisme des arguments
Le curseur de vraisemblance10 invite à graduer la vraisemblance d’une affirmation sur une échelle continue entre 0% et 100%. Cette précaution apportée à notre jugement sur une théorie est bénéfique mais elle disparaît souvent quant on juge les preuves qui soutiennent la théorie : Il n’est pas rare d’entendre que tel argument est soit valide soit invalide; que le manque de rigueur d’un protocole invalide les résultats d’une expérience; que l’on peut jeter un discours puisque l’on y relève l’argument fallacieux n∘21 ou le n∘3711. Il semble cependant que l’on perde de l’information en disqualifiant complètement une preuve imparfaite12. Dans son article critiquant la zététique, Sylvain Poirier écrit: Le fait qu’il y ait des impostures et des erreurs de toutes sortes à la base de certaines affirmations du paranormal ou d’autres choses par les uns ou les autres, ne signifie pas que tout y est faux ni que rien n’aurait pu être effectivement prouvé. Est-il bien raisonnable de considérer la valeur d’un argument comme binaire ? Il semble peu probable qu’un protocole soit parfait tout comme il est peu probable que tout soit à jeter. En replaçant la zététique dans un cadre probabiliste, on quitte le maigre13 {0;1} pour l’infiniment plus riche14 [0,1].
Difficulté de conclure
“Est-il préférable pour la guérison d’une entorse de dormir avec un coussin bleu ou avec un coussin rouge ?”. Face à l’inexistence d’expériences randomisées en double aveugle avec groupe de contrôle, le zététicien doit-il s’enfuir laissant là son jugement suspendu ?
Devant bien des affirmations il semble que les outils de la zététique ne permettent pas de conclure. En particulier, on évoque souvent la hiérarchie suivante : une étude isolée est moins pertinente qu’une méta-analyse et une méta-analyse est moins pertinente que le consensus scientifique15. Mais alors, que dire d’un sujet sur pour lequel il existe peu ou pas d’étude ? Que dire d’un sujet face à un faisceau d’indices réduit et/ou peu rigoureux ? L’approche bayésienne permet de prendre en compte des informations de toutes sortes afin de se faire une opinion.
Et donc ?
L’approche bayésienne offre une perspective qui répond en partie aux critiques sus-citées en permettant de :
- Quantifier la validité d’une information et la probabilité d’une affirmation.
- Corroborer certains des principes dogmatiques de la zététique évoqués ci-dessus
- Replacer le discours zététique dans un langage probabiliste : Utiliser une formule comme « Il est très improbable que X » plutôt qu’un plus catégorique « À l’heure actuelle, il n’y a aucune preuve de X » rend le discours plus humble et plus propice à un échange bienveillant16.
Les apports du bayésianisme
Pour ne pas alourdir l’article la présentation du bayésianisme est assez minimaliste. Le lecteur curieux est invité à se référer aux références données dans l’introduction.
De la formule de Bayes
Le bayésianisme se base sur la formule de Bayes dont il tire son nom. La manière la plus simple d’écrire cette formule est la suivante
(1) ![]()
Les termes ℙ(A|B) et ℙ(B|A) sont des probabilités conditionnelles et se lisent respectivement “Probabilité de A sachant B” et “Probabilité de B sachant A”. La formule de Bayes permet donc simplement de lier les deux probabilités conditionnelles.
Exemple : On considère un lancer de dé, et on cherche à savoir quelle est la probabilité que le dé soit tombé sur 6 sachant que le dé est tombé sur un chiffre pair. On parle donc de probabilité conditionnelle car on cherche la probabilité d’un évènement en connaissant des informations partielles sur cet évènement.
Dans la formule de Bayes 1, on remplace A et B respectivement par “Faire un 6” et “Faire un nombre pair”. On va donc pouvoir calculer ℙ(A|B), la probabilité de “Faire un 6” sachant qu’on a “Fait un nombre pair”, ce qui est bien ce qu’on recherche. On obtient :
![]()
Ce qui se lit : la probabilité que j’ai fait un 6 sachant que j’ai fait un nombre pair est égale à la probabilité de faire un 6 (égale à 1/6) multipliée par la probabilité de faire un nombre pair sachant que j’ai fait un 6 (égale à 1) divisée par la probabilité de faire un nombre pair (égale à 1/2). Ce qui donne :
![]()
que l’on peut facilement vérifier.
À la formule du savoir
Initialement cette formule est un simple outil de calcul de probabilité conditionnelle relativement simple, et c’est ainsi qu’elle est enseignée aux étudiants. Cependant, réinterprétée, notamment par Pierre-Simon de Laplace, elle est devenue un profond principe épistémologique, que certains considèrent comme la formule ultime du savoir17 fondant ainsi le bayésianisme.
Comme nous le verrons, la formule de Bayes permet de calculer la vraisemblance d’une affirmation en fonction de la vraisemblance a priori de cette affirmation et d’une nouvelle information. Autrement dit, elle permet de mettre à jour nos croyances en fonction des preuves que l’on peut rencontrer : témoignage, étude scientifique, reportage TV, article de presse, …
Le théorème dit de Cox-Jaynes permet même de s’assurer que c’est la bonne manière de faire. Ce théorème montre que la logique bayésienne découle de certains prérequis naturels18 et qu’elle est donc indispensable pour manipuler raisonnablement de l’information.
La théorie des probabilités n’est rien d’autre que le sens commun qui fait calcul — Pierre-Simon de Laplace
Retour à la zététique
Nous voilà rendus bien loin des préoccupations zététiques. Mais en apportant une légère modification à la formule de Bayes ci-dessus nous allons y revenir. Changeons tout simplement le A dans la formule par affirmation, et le B par preuve19. Et voilà, nous avons un outil mathématique puissant pour estimer la vraisemblance d’une affirmation à partir de preuves (que ce soit des témoignages, des études, des arguments, …).
Mise en pratique :
![]()
![]() est ce que l’on cherche à évaluer: la vraisemblance d’une affirmation à partir de preuves. Plus précisément, on cherche à calculer l’évolution de la confiance à accorder en une affirmation lorsque une nouvelle preuve est disponible. Cette quantité est aussi appelée probabilité a posteriori puisqu’elle correspond à la vraisemblance de l’affirmation après avoir pris en compte la preuve.
est ce que l’on cherche à évaluer: la vraisemblance d’une affirmation à partir de preuves. Plus précisément, on cherche à calculer l’évolution de la confiance à accorder en une affirmation lorsque une nouvelle preuve est disponible. Cette quantité est aussi appelée probabilité a posteriori puisqu’elle correspond à la vraisemblance de l’affirmation après avoir pris en compte la preuve.
Par opposition, ![]() représente la probabilité a priori. C’est à dire la vraisemblance de l’affirmation avant de prendre en compte la preuve. C’est un des principes fondamentaux du bayésianisme : notre croyance en une affirmation évolue sans cesse en fonction des nouvelles preuves qui nous parviennent.
représente la probabilité a priori. C’est à dire la vraisemblance de l’affirmation avant de prendre en compte la preuve. C’est un des principes fondamentaux du bayésianisme : notre croyance en une affirmation évolue sans cesse en fonction des nouvelles preuves qui nous parviennent.![]() est la probabilité a priori d’observer la preuve. Insistons: ces deux dernières probabilités (
est la probabilité a priori d’observer la preuve. Insistons: ces deux dernières probabilités (![]() et
et ![]() ) sont calculées dans l’état initial des connaissances, c’est-à-dire sans prendre en compte la nouvelle preuve.
) sont calculées dans l’état initial des connaissances, c’est-à-dire sans prendre en compte la nouvelle preuve.
Enfin, la formule de Bayes nous dit que pour trouver ![]() , il nous faut, de plus, la probabilité d’observer cette preuve si l’affirmation est vraie. Cette probabilité est notée:
, il nous faut, de plus, la probabilité d’observer cette preuve si l’affirmation est vraie. Cette probabilité est notée: ![]() , et est également appelée « fonction de vraisemblance », ou simplement « vraisemblance ».
, et est également appelée « fonction de vraisemblance », ou simplement « vraisemblance ».
On peut alors calculer ![]() , la probabilité a posteriori de l’affirmation, c’est-à-dire la confiance à accorder en l’affirmation20 une fois pris en compte les nouveaux éléments de preuve relativement aux connaissances préalables. D’une certaine manière, la formule décrit comment utiliser raisonnablement le curseur de vraisemblance connu des zététiciens.
, la probabilité a posteriori de l’affirmation, c’est-à-dire la confiance à accorder en l’affirmation20 une fois pris en compte les nouveaux éléments de preuve relativement aux connaissances préalables. D’une certaine manière, la formule décrit comment utiliser raisonnablement le curseur de vraisemblance connu des zététiciens.
La dépendance aux connaissances initiales peut sembler gênante puisqu’elle est subjective et risque de faire aboutir deux personnes à des conclusions différentes. Cependant la formule de Bayes assure qu’avec un nombre de preuves suffisant les probabilités a posteriori convergent vers une même valeur quelque soit la probabilité a priori.
Avec ces notations, une affirmation est très probable si ![]() est proche de 1 et inversement très improbable si
est proche de 1 et inversement très improbable si ![]() est proche de 0. De même,
est proche de 0. De même, ![]() proche de 0 correspond à une preuve très improbable dans le cadre initial de nos connaissance donc à une preuve que l’on peut qualifier d’extraordinaire (par ex. « Il a neigé en Août »), alors que
proche de 0 correspond à une preuve très improbable dans le cadre initial de nos connaissance donc à une preuve que l’on peut qualifier d’extraordinaire (par ex. « Il a neigé en Août »), alors que ![]() proche de 1 est une preuve banale c’est à dire une information à laquelle on s’attend (par ex. « Il a neigé en Janvier »).
proche de 1 est une preuve banale c’est à dire une information à laquelle on s’attend (par ex. « Il a neigé en Janvier »).
Avant de voir les avantages du cadre bayésien dans la démarche zététique, voyons un exemple rapide d’utilisation de la formule de Bayes dans un cadre zététique.
Exemple : La maison de mes grand-parents est connue pour être hantée, notamment la vieille chambre du fond. Armé de tout mon courage et de mes solides outils zététique je vais la visiter. J’émets deux hypothèses :
- Affirmation Affirmation
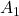 : « Il y a des oiseaux dans les combles à l’origine des phénomènes ». J’y attribue une probabilité de
: « Il y a des oiseaux dans les combles à l’origine des phénomènes ». J’y attribue une probabilité de 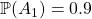 .
. - Affirmation
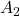 : « Il n’y a pas d’oiseau dans les combles et la maison est vraiment hantée ». J’y attribue une probabilité
: « Il n’y a pas d’oiseau dans les combles et la maison est vraiment hantée ». J’y attribue une probabilité 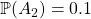 ça paraît fou mais la croyance est tenace dans la famille et dans le village.
ça paraît fou mais la croyance est tenace dans la famille et dans le village.
En arrivant dans la chambre, et non loin en dessous d’une ouverture dans le plafond qui donne accès aux combles, je vois une plume d’oiseau. Voilà ma nouvelle preuve ![]() qui va me permettre de mettre à jour mes croyances. On peut estimer la probabilité de trouver une plume là sachant qu’il y a des oiseaux dans les combles
qui va me permettre de mettre à jour mes croyances. On peut estimer la probabilité de trouver une plume là sachant qu’il y a des oiseaux dans les combles ![]() : c’est commun de trouver des plumes mais encore fallait il qu’elle passe par cette petite ouverture. De même on estime la probabilité de trouver une plume sachant qu’il n’y a pas d’oiseau
: c’est commun de trouver des plumes mais encore fallait il qu’elle passe par cette petite ouverture. De même on estime la probabilité de trouver une plume sachant qu’il n’y a pas d’oiseau ![]() : c’est très peu probable, il aurait fallu que quelqu’un l’amène ici. On peut enfin calculer la probabilité de trouver une plume
: c’est très peu probable, il aurait fallu que quelqu’un l’amène ici. On peut enfin calculer la probabilité de trouver une plume ![]() grâce à la formule suivante21:
grâce à la formule suivante21: ![]() .
.
On peut maintenant appliquer la formule de bayes pour ![]() et
et ![]() .
.
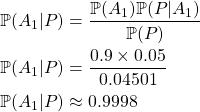
et
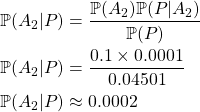
Après mise à jour des vraisemblances j’attribue donc une probabilité de ![]() pour l’affirmation
pour l’affirmation ![]() et
et ![]() pour l’affirmation
pour l’affirmation ![]() .
.
Évidemment faire une telle analyse chiffrée n’est pas possible au quotidien et ce n’est même pas utile à vrai dire. Mais il est très bénéfique d’adopter une pensée bayésienne en prenant l’habitude de mettre à jour la vraisemblance de nos croyances et en musclant notre intuition bayésienne22.
On peut maintenant voir en quoi cette approche permet de répondre aux critiques formulées dans la section précédente :
- Elle peut être utilisée pour justifier les principes a priori arbitraires de la zététique. Puisque le théorème de Cox-Jaynes montre que l’approche bayésienne est la seule cohérente, alors démontrer les principes zététiques par la formule de Bayes justifierait leur pertinence. C’est ce que nous ferons dans la dernière section pour deux de ces principes.
- Puisque dans l’approche bayésienne tout est exprimé en fonction de probabilité on évite la binarité et la rigidité que peut prendre parfois le discours zététique.
- Comme nous le verrons dans la dernière section, en plus de justifier le rasoir d’Ockham et la maxime de Hume, l’approche bayésienne apporte un cadre mathématique qui permet de quantifier ce qu’on entend par « l’hypothèse la plus parcimonieuse » ou une « affirmation extraordinaire ».
- Alors que la zététique requiert parfois une étude approfondie d’un sujet pour obtenir une conclusion, l’approche bayésienne permet toujours d’attribuer une vraisemblance à l’affirmation quel que soit la quantité d’information dont on dispose.
Les outils zététiques dans une main bayésienne
Les deux premières parties ont permis de montrer ce que le bayésianisme peut apporter à la zététique et s’alignent avec des travaux pré-existants (notamment ceux de Christophe Michel présenté dans l’introduction). Cette dernière partie est une contribution plus personnelle (et plus technique aussi peut-être) et montre comment le cadre bayésien permet de justifier deux principes fondamentaux de la zététique : le rasoir d’Ockham et la maxime de Hume répondant ainsi partiellement23 à la première critique formulée.
Rasoir d’Ockham
Quand on est confronté à plusieurs affirmations expliquant un même phénomène, le rasoir d’Ockham nous invite à privilégier l’affirmation la plus parcimonieuse. C’est à dire, l’affirmation qui requiert les hypothèses les moins coûteuses intellectuellement. Cependant, la signification de parcimonie ne va pas toujours de soi en l’absence de quantifications.
Voyons ce que l’approche bayésienne peut en dire. Admettons que l’on ait trois affirmations ![]() ,
, ![]() et
et ![]() pour expliquer la même preuve P. les formules de Bayes s’écrivent alors :
pour expliquer la même preuve P. les formules de Bayes s’écrivent alors :
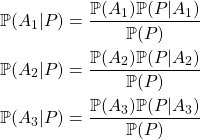
Chercher l’affirmation à privilégier revient à chercher l’affirmation la plus probable au vu de la preuve, donc la plus grande de ces trois probabilités. En multipliant toutes ces quantités par ![]() , on cherche donc l’affirmation maximisant
, on cherche donc l’affirmation maximisant ![]() .
.
Ce qui peut se lire : Probabilité de l’affirmation ![]() multipliée par la probabilité d’observer la preuve
multipliée par la probabilité d’observer la preuve ![]() sachant que l’affirmation
sachant que l’affirmation ![]() est vraie. La formule de Bayes nous dit donc comment interpréter le terme « plus parcimonieux » du rasoir d’Ockham. Ce n’est donc pas simplement l’affirmation la plus probable qu’il faut privilégier, c’est à dire
est vraie. La formule de Bayes nous dit donc comment interpréter le terme « plus parcimonieux » du rasoir d’Ockham. Ce n’est donc pas simplement l’affirmation la plus probable qu’il faut privilégier, c’est à dire ![]() , mais bien le produit de cette probabilité avec la probabilité d’observer
, mais bien le produit de cette probabilité avec la probabilité d’observer ![]() sachant que
sachant que ![]() (l’exemple à venir rendra la nuance plus claire). On peut en déduire une nouvelle formulation pour le rasoir d’Ockham:
(l’exemple à venir rendra la nuance plus claire). On peut en déduire une nouvelle formulation pour le rasoir d’Ockham:
Rasoir d’Ockham bayésien :L’hypothèse maximisant ![]() doit être privilégiée. C’est à dire l’hypothèse maximisant le produit de la probabilité de
doit être privilégiée. C’est à dire l’hypothèse maximisant le produit de la probabilité de ![]() et de la probabilité d’observer la preuve
et de la probabilité d’observer la preuve ![]() sachant
sachant ![]() .
.
Cela peut sembler être une subtilité mais l’exemple suivant montre la différence induite par ce changement.
Exemple : Monsieur M. met dans une boite un chat et un souris. Dix secondes après il rouvre la boîte et la souris a totalement disparu. On peut émettre plusieurs affirmations :
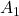 = Le chat a mangé la souris
= Le chat a mangé la souris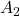 = La souris est passé dans une dimension différente pour échapper au chat
= La souris est passé dans une dimension différente pour échapper au chat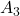 = Monsieur M. est magicien
= Monsieur M. est magicien
Usons de notre rasoir d’Ockham bayésien pour voir quelle affirmation privilégier. On considère les probabilités a priori des affirmations suivantes : ![]() : Les chats aiment manger des souris;
: Les chats aiment manger des souris;![]() : Je n’ai pas connaissance de souris ayant une telle capacité;
: Je n’ai pas connaissance de souris ayant une telle capacité;![]() : Je ne connais pas bien cette personne, mais il n’est pas impossible que ce soit un tour de magie.
: Je ne connais pas bien cette personne, mais il n’est pas impossible que ce soit un tour de magie.
- Si on s’intéresse au curseur de vraisemblance utilisé classiquement en zététique, nous pourrions penser qu’il ne faut considérer que la probabilité a priori
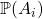 de ces affirmations. Ainsi il semblerait que l’affirmation
de ces affirmations. Ainsi il semblerait que l’affirmation 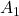 soit à privilégier.
soit à privilégier. - Considérons désormais la seconde partie du calcul uniquement (celle qui prend en compte la probabilité d’observer la donnée si l’affirmation est vraie), et que nous appelons la fonction de vraisemblance ou simplement vraisemblance. La donnée en l’occurrence est la révélation du contenu de la boite 10 secondes plus tard sans souris. On a alors par exemple :
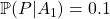 : Seulement 10 secondes pour manger une souris et ne laisser aucune trace… ça me parait suspect;
: Seulement 10 secondes pour manger une souris et ne laisser aucune trace… ça me parait suspect; 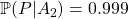 : Si la souris avait un tel pouvoir elle aurait en effet sûrement disparu;
: Si la souris avait un tel pouvoir elle aurait en effet sûrement disparu; 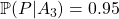 : Si Monsieur M. est magicien alors il est très probable que la disparition de la souris soit son tour de magie. En ne regardant que cette « vraisemblance », c’est alors le voyage inter-dimensionnel qui est à privilégier.
: Si Monsieur M. est magicien alors il est très probable que la disparition de la souris soit son tour de magie. En ne regardant que cette « vraisemblance », c’est alors le voyage inter-dimensionnel qui est à privilégier.
- Dans un cadre bayésien, c’est la probabilité a posteriori que nous devrions regarder. C’est le produit des deux quantités précédentes24. On trouve alors :
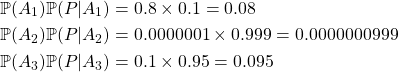
Au final, l’hypothèse à privilégier est que Monsieur M. est magicien…
Dans l’utilisation classique du rasoir d’Ockham cette précision n’est pas faite et le terme « affirmation la plus parcimonieuse » peut prêter à confusion.
On peut donc résumer le calcul ainsi :
![]()
Les termes posterior et prior sont communément utilisés dans le cadre bayésien comme indiqué dans la formule ci-dessus.
Maxime de Hume
Également appelée standard de Sagan, ou de Truzzi, ou de De Laplace25, cette maxime postule que « Une affirmation extraordinaire requiert une preuve extraordinaire ».
Ici encore, nous allons voir que le cadre bayésien permet de retrouver et de préciser cette affirmation. Reprenons à nouveau la formule de Bayes :
(2) ![]()
Comme dit précédemment une affirmation est dite extraordinaire si elle est a priori très peu probable. Une telle affirmation vérifie donc ![]() , où
, où ![]() est une quantité très petite. Pour que cette affirmation, une fois pris en compte le nouvel élément de preuve, soit vraisemblable, il faut donc une preuve qui mène à
est une quantité très petite. Pour que cette affirmation, une fois pris en compte le nouvel élément de preuve, soit vraisemblable, il faut donc une preuve qui mène à ![]() . On peut montrer que cette condition26 implique la relation suivante:
. On peut montrer que cette condition26 implique la relation suivante:
(3) ![]()
Ainsi pour qu’une affirmation a priori extraordinaire devienne vraisemblable il faut donc que la probabilité d’observer la preuve soit beaucoup plus petite que la probabilité d’observer la preuve sachant l’affirmation (nous verrons un exemple plus loin). La formule de Hume se déduit simplement en observant que comme toute probabilité est inférieur ou égale à ![]() on a
on a ![]() et donc
et donc
(4) ![]()
Ainsi la probabilité d’observer la preuve doit être très petite. En d’autres terme, la preuve doit être extraordinaire27 ! Ainsi, la formule de Bayes permet bien de démontrer la maxime de Hume.
Cependant la formule (3) en dit un petit peu plus :
la condition, ![]() n’est pas suffisante ! Il faut également que
n’est pas suffisante ! Il faut également que ![]() et donc que la probabilité d’observer la preuve sachant l’affirmation ne soit pas trop petite ! C’est à dire qu’il faut que la preuve soit ordinaire si l’affirmation est vraie :
et donc que la probabilité d’observer la preuve sachant l’affirmation ne soit pas trop petite ! C’est à dire qu’il faut que la preuve soit ordinaire si l’affirmation est vraie : ![]() .
.
On peut en déduire une nouvelle formulation pour la maxime de Hume.
Maxime de Hume bayésienne : Une affirmation extraordinaire requiert une preuve extraordinaire. Mais il faut aussi que la preuve soit ordinaire si l’affirmation est vraie.
Exemple :
Considérons l’affirmation ![]() « les licornes existent » que l’on peut qualifier d’extraordinaire. J’y octroie a priori une probabilité de un sur un milliard :
« les licornes existent » que l’on peut qualifier d’extraordinaire. J’y octroie a priori une probabilité de un sur un milliard : ![]() Pour que cette affirmation paraisse crédible, il faut donc observer une preuve
Pour que cette affirmation paraisse crédible, il faut donc observer une preuve ![]() vérifiant
vérifiant ![]() .
.
Considérons par exemple la preuve ![]() : « Quelqu’un a vu de loin une silhouette de cheval avec une corne sur le front ». Ce n’est pas une preuve si extraordinaire : il a pu se tromper, c’était peut-être une installation artistique, des petits malins ont pu attacher un postiche ou il a menti. J’estime la probabilité d’observer cela à un sur mille. On a donc
: « Quelqu’un a vu de loin une silhouette de cheval avec une corne sur le front ». Ce n’est pas une preuve si extraordinaire : il a pu se tromper, c’était peut-être une installation artistique, des petits malins ont pu attacher un postiche ou il a menti. J’estime la probabilité d’observer cela à un sur mille. On a donc ![]() . En revanche, il est clair que la probabilité que quelqu’un ait vu de loin une silhouette de cheval avec une corne sur le front sachant que les licornes existent est très élevée :
. En revanche, il est clair que la probabilité que quelqu’un ait vu de loin une silhouette de cheval avec une corne sur le front sachant que les licornes existent est très élevée : ![]() .
.
On peut maintenant appliquer la formule de Bayes pour mettre à jour ma croyance en ![]() sachant
sachant ![]() :
:
![]()
Après cette preuve, j’octroie à l’existence des licornes une crédence de un sur un million. Cette preuve satisfaisait donc un seul des deux critères de la maxime de Hume bayésienne : elle est ordinaire si l’affirmation est vraie mais elle n’est pas extraordinaire en soi.
Au contraire prenons une autre preuve ![]() qui a une chance sur un milliard d’être observée : « J’ai fait 30 piles de suite ». La preuve est bien extraordinaire
qui a une chance sur un milliard d’être observée : « J’ai fait 30 piles de suite ». La preuve est bien extraordinaire ![]() . Mais là encore la preuve ne satisfait qu’un seul des deux critères de la maxime de Hume baysésienne : elle est extraordinaire mais elle n’est pas ordinaire si l’affirmation est vraie. En effet, ici les deux évènements sont décorrélés : l’existence de licorne ne rend pas plus ordinaire une suite de 30 piles
. Mais là encore la preuve ne satisfait qu’un seul des deux critères de la maxime de Hume baysésienne : elle est extraordinaire mais elle n’est pas ordinaire si l’affirmation est vraie. En effet, ici les deux évènements sont décorrélés : l’existence de licorne ne rend pas plus ordinaire une suite de 30 piles ![]() . Ça ne suffit donc pas à me convaincre. En l’occurrence la formule de Bayes donne:
. Ça ne suffit donc pas à me convaincre. En l’occurrence la formule de Bayes donne:
![]()
Ce deuxième cas est caricatural mais il soulève une erreur de logique : se contenter d’une preuve extraordinaire sans vérifier que cette preuve est beaucoup plus probable dans l’affirmation qu’elle cherche à valider.
Enfin une preuve satisfaisante pourrait donc être ![]() un article scientifique corroboré par plusieurs chercheurs et fournissant suffisamment d’informations sur l’existence de licornes et étayé par des vidéos et des photos. Une telle preuve serait tout à fait extraordinaire en soi (estimée pour l’exemple à une chance sur 800 millions) et totalement ordinaire si l’affirmation est vraie (estimée ici à
un article scientifique corroboré par plusieurs chercheurs et fournissant suffisamment d’informations sur l’existence de licornes et étayé par des vidéos et des photos. Une telle preuve serait tout à fait extraordinaire en soi (estimée pour l’exemple à une chance sur 800 millions) et totalement ordinaire si l’affirmation est vraie (estimée ici à ![]() ). La formule de Bayes donne alors :
). La formule de Bayes donne alors :
![]()
Conclusion
Voilà donc quelques idées sur la complémentarité entre bayésianisme et zététique. Nous avons montré d’abord quelques écueils possible de la démarche zététique et comment le cadre bayésien permets en partie d’y répondre. Dans une dernière partie nous avons montré comment la formule de Bayes permet de retrouver et préciser deux principes de la zététique : le rasoir d’Ockham et la maxime de Hume.
Bien d’autres pièces restent à ajouter au puzzle afin d’obtenir un paradigme plus solide. Quid des autres principes de la zététique ? Des biais cognitifs et des sophismes ? Quid de la charge de la preuve ? Est-ce que la perspective bayésienne permet d’en dire quelque chose, voire d’enrichir ces concepts ? Néanmoins, à l’avenir, si votre recette zététique semble mécontenter votre auditoire, essayer d’y rajouter une pincée de bayésianisme pour la rendre plus légère.
- https://medium.com/mon-oeil
- Bayésianisme sur sa chaîne science4all.
- Axiome avec Thibault Giraud et Probablement? avec divers invités
- La pensée bayésienne et Le sophisme du procureur ((et quelques autres leçons Bayésiennes))
- Maladies rares : l’apport de la formule de Bayes
- La loi de Bayes
- Voici trois exemples de travaux critiquant l’approche zététique :
- Naqimon Weil – Esprit Critique en toc (2017)
- Sylvain Poirier – La zététique sujette à des dérives pseudos scientifiques
- La vidéo La décadence de la zététique par Mouton Lucide (à noter que ce dernier est revenu sur ses propos suite à son entretien avec Samuel Buisseret)
D’autres vidéastes, comme Hypno machine ou Charles Robin ont également partagé des critiques de la zététique. Certains arguments intéressants ont été repris ici.
- Thomas Durand et Vled Tapas (La Tronche en Biais) en propose également une liste dans la vidéo Y’en a marre des zététiciens
- Proposition de traduction : Comme tous les outils, le kit de détection de balivernes peut être mal utilisé, utilisé dans un mauvais contexte voire se substituer à la réflexion. Mais appliqué judicieusement, il peut faire la plus grande différence, notamment dans l’évaluation de nos propres arguments avant de les présenter aux autres.
- Voir par exemple la vidéo « Curseur de vraisemblance » d’Henri Broch.
- En réalité, c’est un argument fallacieux en soi de n’attaquer que la forme du discours. Dans sa liste de moisissures argumentatives le Cortecs l’appelle « Attaque sur la forme »
- Encore une fois, je ne pense pas que ce soit dans les fondements de la zététique mais que ce sont plutôt des « mauvaises pratiques » qui émergent souvent chez les aspirants zététiciens.
- Ensemble contenant seulement les valeurs 0 et 1, que l’on peut interpréter comme vrai/faux ou valide/invalide.
- Ensemble comprenant tous les réels entre 0 et 1 et donc infiniment plus de nuances entre vrai et faux entre valide et invalide.
- Toutefois, notons que la méta-analyse n’est pas exempte de tout biais. L’article On bias and precision in meta analysis: The error in the error montre comment les biais des études originelles sont transmises à la méta-analyse.
- L’humilité épistémique présentée par exemple dans l’article L’humilité épistémique, la clef pour convaincre éthiquement semble être intéressante pour communiquer efficacement comme le soutien l’étude The effects of communicating uncertainty on public trust in facts and numbers de l’université d’Oslo.
- La formule du savoir de Lê Nguyen Hoang.
-
-Consistance : s’il existe plusieurs façons de trouver un résultat, elles doivent aboutir au même résultat
-Continuité de méthode : un changement de valeur d’un paramètre ne doit pas obliger à changer de méthode de calcul
-Universalité : on désire un calculateur de situations général, non destiné à un usage particulier
- Dans la suite de l’article, nous utiliserons uniquement les termes « affirmation » et « preuve » par souci de consistance. Cependant le premier peut être substituer par « théorie » et le deuxième par « information », « données », « argument ».
- Cette confiance à accorder est aussi appelée crédence en l’affirmation
- Cette formule fonctionne sous réserve que
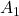 et
et 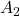 soient les deux seuls possibilités.
soient les deux seuls possibilités. - Voir la vidéo Maîtrisez l’intuition bayésienne !! sur Science4All.
- D’autres principes zététiques restent à justifier
- Notons qu’il faudrait encore diviser par
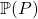 pour terminer le calcul et avoir la vraie probabilité de chaque affirmation. Mais ce calcul est suffisant pour comparer les différentes affirmations
pour terminer le calcul et avoir la vraie probabilité de chaque affirmation. Mais ce calcul est suffisant pour comparer les différentes affirmations - Cours « Zététique & autodéfense intellectuelle » de Richard Monvoisin, cours 4 épisode 4
- En reprenant la formule~(2) :
ce qui mène au résultat.
- Il est commun d’interpréter preuve extraordinaire dans le sens de preuve solide, robuste (tel qu’une étude scientifique) plutôt que dans le sens de preuve très improbable. En réalité, ces deux interprétations sont tout à fait compatibles. Pour s’en convaincre il suffit de voir qu’une preuve faible (témoignage, légende) d’une affirmation improbable est probable et qu’une preuve solide d’une affirmation probable (météo, actualité) est également probable. Par contraposée, on en déduit qu’une preuve solide (photo, vidéo, étude scientifique) d’une affirmation très improbable (licorne, extra-terrestre, EMI) est forcément très improbable.