Archives des Zététique

Chemtrails, subitisation, musicothérapie, lapin qui saute… le best of des dossiers étudiants 2022/2023

10 août 202329 août 2023 Nicolas Martin et Viven Soldé

Les formations proposées par le CORTECS sont souvent l’occasion de faire travailler des étudiant·e·s sur des projets zététiques. Ces dossiers sont de qualité variable : on comprend (et on regrette) que la charge de travail des étudiant·e·s ne leur laisse pas beaucoup de place pour les yétis, les fantômes et autres monstres de la raison. Mais parfois, certains travaux sont très bons et méritent largement d’être rendus publics pour profiter à tout le monde. S’ils ne sont pas infaillibles (mais aucun travail ne l’est) ils font preuve d’une rigueur et d’une démarche critique qui nous semblent satisfaisantes.
Vous trouverez donc sur cette page quelques-uns des meilleurs dossiers produits par les étudiant·e·s des formations zététique du Cortecs en 2022 – 2023. Les premiers proviennent des cours donnés à l’école d’ingénieur ENSEEIHT à Toulouse par Nicolas Martin, les suivants sont issus d’un cours donné à l’Institut d’enseignement à distance en Sciences de l’éducation de l’Université Paris 8 par Vivien Soldé.

Table of Contents

Cours à l’ENSEEIHT

Etude de l’influence de la couleur d’éléments sur leur subitisation

[Télécharger ici] Par L. Bahroun, A. Ecorce, N. Bertheloot, N. Groenen

La subitisation c’est la capacité à percevoir le nombre d’éléments dans un ensemble « d’un seul coup d’œil », sans les compter individuellement. Comme les cure-dents dans Rain Man vous voyez. D’ailleurs cette capacité est probablement une légende, et des études montrent que les autistes auraient d’ailleurs de moins bonnes capacité de subitisation ¹.

Mais là n’était pas la question. Il s’agissait ici de savoir si la subitisation est plus facile si les éléments à compter sont de couleurs différentes. La taille d’échantillon n’est pas énorme, mais les résultats semble montrer que oui, la bicoloration facilite la subitisation (j’aime bien cette phrase). Une chouette expérience à répliquer et à décliner !

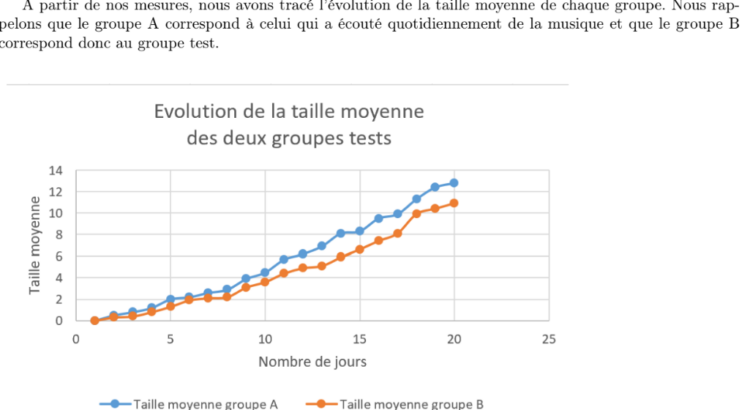
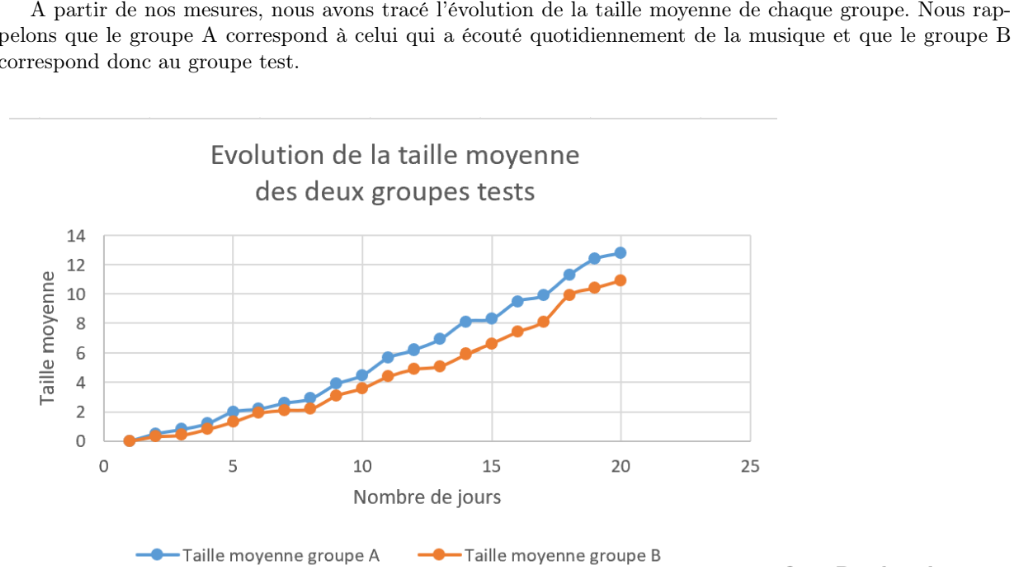
La musicothérapie (et influence de la musique sur la pousse des plantes)

[Télécharger ici] Par T. El Hadi, T. Haas, S. Léostic, D. Zribi

Les cactus poussent-ils mieux en écoutant Jacques Dutronc ?
Les étudiants ont dans un premier temps présenté les prétentions et un peu de littérature sur la musicothérapie. Ils ont ensuite voulu voir si la musique influençait la pousse de lentilles. Le protocole est très chouette mais pas parfait (pas de double aveugle, petit échantillon, plusieurs risques de biais) mais il semble que oui les plantes exposées à la nocturne n°2 de Chopin, ont bien poussé plus vite… surprenant ! Reste à essayer de comprendre ce qui a vraiment joué et si ça marcherait aussi bien avec du NTM.

Influence de la construction d’un sondage sur les réponses des participants

[Télécharger ici] Par C. Olivi, A. Wagret et C. Serre
L’ordre dans lequel les questions sont posées dans un sondage peut-il influencer les réponses des participants. On y parle de l’effet entonnoir; de l’effet de contexte logique et de l’effet de contexte sémantique.
Bien que l’analyse statistique aurait pu être plus précise, l’étude semble bien montrer une influence (dans le sens inverse de ce qui avait été prédit). Le recul critique sur l’étude est bien montré.

La génération de l’aléatoire par le cerveau et les manières de l’influencer

[Télécharger ici] Par L. Baldet, B. Berlin, G. Laumonier, M. Lourenco

Le cerveau est mauvais générateur d’aléatoire, on le sait. Si on demande de générer un nombre entre 1 et 10, chaque valeur n’a pas la même chance d’être donnée.
Mais y a-t-il une différence si on demande de penser, de choisir ou de sélectionner un nombre au hasard ? Apparemment oui !

Illusion sensorielle – Effet cutané du lapin (ECL)

[Télécharger ici] Par L. Seugnet, E. Massol, A. Goodwin, S. D’alimonte, E. Norroy

L’illusion cutanée du lapin qui saute est une illusion au nom très marrant et qu’il est vraisemblablement très difficile à observer. Pour ma part, je l’ai longtemps cherchée mais jamais réellement observée. C’est mon big foot à moi. Alors j’ai proposé à un groupe d’étudiant·e·s de partir à sa recherche avec méthode : en fouillant la littérature pour essayer de le mettre en évidence… sans grand succès. Cette illusion serait-elle illusoire ? Le mystère demeure.

Encore un grand bravo à toutes les étudiantes et étudiants et un grand merci : j’apprends beaucoup grâce à vous. Merci aussi à celles et ceux qui ne sont pas ici. On sait que vous aimeriez avoir plus de temps pour parler de yéti et de fantôme !

Cours à l’IED ² de Paris 8

Chemtrails, analyse d’une théorie complotiste

[Télécharger par ici] par E. Lépine Bazzucchi

Cette étudiante s’intéresse à la construction de la théorie des chemtrails grâce à un
ensemble de documents écrits, photos, audios et vidéos venant du web. Tout au long de ce travail, elle remet en cause ses certitudes, et si les arguments des partisans des chemtrails ne la convainquent pas, certaines ouvertures autour des épandages de pesticides et de la géo-ingénierie la laissent plus dubitative…

L’esprit jubile : recension de la BD « L’esprit critique »

26 mars 202326 mars 2023 Viven Soldé

Qu’est-ce que l’esprit critique ? On pense tous l’avoir mais sait-on vraiment le définir ? C’est la question à laquelle ont voulu répondre Isabelle Bauthian (biologiste de formation, scénariste et rédactrice culturelle et scientifique) et Gally (dessinatrice) dans cette bande-dessinée publiée aux éditions Delcourt (130 pages). Et… c’est tout bonnement une petite merveille !

Case issue de la bande-dessinée *L’esprit critique* de Isabelle Bauthian et Gally, Octopus, Delcourt, 2021, p. 4.

D’un point de vue narratif et esthétique

Lors d’une soirée, Paul rencontre une jeune femme qui se présente comme druide. Après une discussion animée autour de photos de fées, Paul rentre chez lui, se connecte sur ses réseaux sociaux et déverse sa haine de l’irrationnel. C’est alors qu’il apparaît, enfin… elle : L’esprit critique !

On prend énormément de plaisir à faire un bout de chemin avec ces personnages extrêmement attachants. Paul, croyant en La science sans aucune méthode, perdu dans la complexité du monde qui s’ouvre devant lui grâce à Elle, doppelgänger métamorphe critique aux cheveux roses qui donne au lecteur une soif de connaissance comme jamais. Paul, c’est tout simplement nous qui découvrons cet univers de l’esprit critique. Il exprime nos interrogations et nos doutes sur cette conception à laquelle nous n’avons pas forcément beaucoup réfléchit. Elle, elle est l’incarnation de l’esprit critique et de sa perfectibilité.

Grâce à ses pouvoirs elle fait sortir Paul de son petit confort, de sa petite routine pour l’emmener vers des contrées inconnues (voyage dans le temps et dans l’espace). L’odyssée de Paul commence avec une plongée dans l’histoire des sciences, des bâtons d’Ishango à Kepler et Galilée en passant par les philosophe grecs (Platon, Thalès, Aristote, Ptolémée Anaximandre de Millet, etc.). On regrette juste l’absence d’une excursion auprès des premiers sceptiques à l’instar de Pyrrhon d’Élis. Le voyage de notre personnage se poursuit ensuite sur la méthode scientifique moderne (évaluation des hypothèses, principe de réfutabilité, notion de preuve, pseudo-sciences, etc.) puis sur la déconstruction partielle de nos systèmes cognitifs principalement avec l’approche des biais (tous représentés de manière très parlante). Le périple continue avec les méthodes d’évaluation de l’information (approches des statistiques, théière de Russell, évaluation d’une étude scientifique, sophismes, etc.) et se conclut sur une note de tolérance et sur les limites de l’esprit critique (distinction entre faits et foi, valeurs, importance des émotions, différences de points de vue idéologiques, politiques et sociaux).

Planche issue de la bande-dessinée *L’esprit critique* de Isabelle Bauthian et Gally, Octopus, Delcourt, 2021, p. 21.

D’un point de vue éducatif et pédagogique

L’alchimie du couple, l’humour malicieux, la bienveillance, la douceur du trait de Gally, la joie qui se dégage de cette BD… nous rend tous simplement heureux. C’est bête à dire, mais particulièrement pertinent dans un ouvrage qui veut nous faire sortir de notre zone de confort. Une tendresse véritable alimente des représentations réfléchies et travaillées en particulier au niveau du genre. Elle, l’esprit critique, est à la fois professeure, chercheuse, super-héroïne, militaire, dragonne, étudiante, etc. Autant de modèles hautement positifs et encourageants pour des secteurs où les femmes sont encore peu représentées allant de pair avec une mise en avant de femmes scientifiques (notamment l’astronome américaine Maria Mitchell) trop souvent invisibilisées par une historiographie grandement patriarcale.

C’est une mine d’or pour qui veut commencer à modeler son esprit critique avec des outils précis quoiqu’un peu survolés. Histoire des sciences et des idées, fonctionnement de la recherche moderne, biais cognitifs, sophismes et paralogismes, etc. Presque tout y est. Chaque planche, chaque case est d’une richesse incroyable. Certaines fonctionnent parfaitement en solitaire et pourraient être affichées dans les écoles, les collèges et les lycées (coup de cœur pour la planche de la « Méthode scientifique moderne »). On regrettera peut-être le rythme extrêmement intense de la BD qui transcrit l’enthousiasme de ses autrices mais sans doute trop soutenu pour un néophyte qui commencerait à s’y intéresser et qui devra sans aucun doute reprendre ses lectures plusieurs fois. Peut-être que plusieurs tomes auraient pu être à la fois plus détaillés et prendre plus de temps sur certains concepts. Mais ce n’est pas tellement gênant finalement puisque cette lecture est tellement plaisante qu’on prendra beaucoup de bonheur à s’y replonger.

En ce qui concerne « La » science, on aurait aimé une approche plus précise notamment des différents modes de construction des connaissances et non pas uniquement de la méthode hypothético-déductive ; et donc plutôt une approche « des » sciences. Par exemple, on regrettera, page 44, la formulation : « La science moderne est objective, expérimentale et autocorrective ». En effet, concernant l’objectivité, la sociologie des sciences nous a démontré le contraire ; tandis qu’au niveau de l’expérimentation, elle n’est pas l’apanage de tous les domaines. Quid de l’histoire, de la sociologie, etc.

Il faut donc voir cet ouvrage comme une vaste introduction, qui permettra au lecteur novice de savoir où creuser pour affiner ses outils de réflexion et de compréhension du monde. Et ça, c’est déjà pas mal !

Planche issue de la bande-dessinée *L’esprit critique* de Isabelle Bauthian et Gally, Octopus, Delcourt, 2021, p. 46-47.

D’un point de vue humaniste

La bienveillance et la tendresse ne sortent pas de nulle part, mais bien d’une très grande confiance en l’être humain et en ses capacités. Dans cette époque morose où nous sommes submergés d’information, où les polémiques s’enchaînent, où la société se divise, où l’univers médiatique appuie l’idée que l’irrationalité semble l’emporter… c’est une sublime bouffée d’air frais. Nous pouvons changer, nous en tant qu’être humain, et finalement changer la société qui nous entoure en nous basant sur des outils simples et dont l’efficacité est vérifiable sans forcément se mettre au-dessus de la mêlée. Pratiquer l’esprit critique ce n’est pas devenir une machine apathique mais au contraire comprendre et maîtriser ses émotions « nécessaires au raisonnement ». Pratiquer l’esprit critique ce n’est pas défendre le scientisme, mais connaître les limites de nos connaissances et tracer la frontière entre les faits et nos opinions (même si les autrices préfère le terme « foi ») . On regrette un peu que les philosophies des lumières et leurs apports essentiels à l’émancipation des sciences n’aient pas été abordées, mais on pardonne facilement au vu de la richesse des connaissances déjà présentes.

Planche issue de la bande-dessinée *L’esprit critique* de Isabelle Bauthian et Gally, Octopus, Delcourt, 2021, p. 56.

Pour conclure

En bref, on rigole, on est ému, on apprend, on voyage… C’est une véritable aventure initiatique à mettre entre toutes les mains… Bon, à partir d’un certain âge peut-être parce qu’assez ardue. De plus, certains concepts sont illustrés de manière… originale. L’explication de la différence entre moyenne et médiane avec la b*** de Rocco Siffredi reste mon préféré. Beaucoup de choses pourront vous sembler floues, complexes, dures à conceptualiser, mais ce n’est que le début de votre expédition en terre inconnue. Avec un peu de recherches extérieures pour recouper les sources – exercice ô combien sain et indispensable – vous arriverez à vous y retrouver. De plus, la bande dessinée propose une bibliographie et une section « pour aller plus loin ».

Pour les autres, ceux déjà rompus à l’exercice, vous y redécouvrirez les marottes du scepticisme et vous amuserez à trouver les différents easter egg zététiques et références geeks cachées un peu partout. Mais pour approfondir vos connaissances sur le sujet, ce n’est sans doute pas l’objet adapté. Dans tous les cas, si vous êtes convaincu, courez l’acheter et faites vivre ses autrices ; si vous n’êtes pas convaincu, courez l’acheter parce que vous manquez sans doute d’esprit critique. Comment ça un faux dilemme ?

Cases issues de la bande-dessinée *L’esprit critique* de Isabelle Bauthian et Gally, Octopus, Delcourt, 2021, p. 93.

Best of dossiers étudiants 2021/2022

4 juillet 20224 juillet 2022 Nicolas Martin

Les formations proposées par le CORTECS sont souvent l’occasion de faire travailler des étudiant·e·s sur des projets zététiques. Ces dossiers sont de qualité variable : on comprend (et on regrette) que la charge de travail des étudiants ne leur laisse pas beaucoup de place pour les yétis, les fantômes et autres monstres de la raison. Mais parfois, certains travaux sont très bons et méritent largement d’être rendu public pour profiter à tout le monde. S’ils ne sont pas infaillibles (mais aucun travail ne l’est) ils font preuve d’une rigueur et d’une démarche critique qui nous semblent satisfaisants.
Vous trouverez donc sur cette page quelques-uns des meilleurs dossiers produits par les étudiants des formations zététique du Cortecs en 2022.

La Théorie du ruissellement [Télécharger] par Mohamed M’hand, Philippe Négrel-Jerzy, Sébastien Pont et Edgar Remy de l’ENSEEIHT
« La révélation des pyramides », comment les documentaires peuvent-ils nous manipuler ? [Télécharger] par Nathan Vergé, Natália Rafaele, Christophe Pantel et Pablo Neyens de l’ENSEEIHT
Étude des prévisions astrologiques [Télécharger] par HUC-LHUILLERY Alexia, HENRIOT Lauriane, LHEOTE Quentin et FAUCHEUX Tanguy de l’ENSEEIHT
Manipulation de graphiques [Télécharger] par les L1 en psychologie de l’université de Nîmes
Les effets de la lithothérapie sur l’anxiété et les troubles du sommeil [Télécharger] par les L1 en psychologie de l’université de Nîmes
La méditation de pleine conscience et ses bienfaits sur le sommeil [Télécharger] par les L1 en psychologie de l’université de Nîmes

Merci et félicitations à elles et eux.

Quand faut-il dépendre son jugement ? Ou l’objectif du scepticisme

28 mars 202229 juillet 2024 Nicolas Martin

La vérité est au fond du puits, nous dit-on³.
Voilà ce que nous répètent les sceptiques de tout poil depuis la nuit des temps : illusions d’optique, faux souvenirs, erreurs de jugement, limites de notre langage, erreurs de logique, sophisme, conformisme social, bulles de filtre, constructions socio-culturelles et toujours la possibilité d’un rêve, d’une simulation ou d’un malin génie, … et puis si ça se trouve vous n’êtes qu’un papillon en train de rêver d’être un humain⁴.
Les distorsions de l’information sont nombreuses et apparaissent à toutes les échelles. Il est alors tentant, à la manière de Pyrrhon, de sombrer dans l’indifférence, de ne donner pas plus de crédit à ceci qu’à cela, et laisser son jugement suspendu pour toujours. Ou alors il faut décider de dépendre son jugement – si celui-ci est suffisamment affiné.
Cet article propose quelques pistes de réflexion sur cet acte crucial dans la démarche sceptique : la dépendaison du jugement.

Table of Contents

Juger et choisir

La vérité est au fond du puits, vous dis-je. Et il y a une solution toute trouvée : n’allons plus au puits. L’univers qui m’entoure m’est éternellement inaccessible – et encore, même ceci n’est pas certain – il n’y a pas de raison d’aller y chercher une quelconque vérité.

C’est, en tout cas, la réponse qu’apporte la première grande école du scepticisme¹, celle de Pyrrhon, qui suspend son jugement aussi vite qu’il le peut. « Épochè« , nous dit-il². C’est la suspension, l’interruption, l’arrêt du jugement. Alors, on s’assoit sur le bord de la réalité et on la regarde défiler.

Appliquer cette doctrine à des enjeux actuels donnerait quelque chose comme ça : Catastrophes écologiques ? Mouais, peut-être ; Inégalités sociales ? Pas plus que ça ; Covid ? J’en sais rien ; Guerre en Ukraine ? Je m’abstient³ ; Tu boiras quand même un petit coup ? Bof, à la rigueur.

Pyrrhon ira voter blanc. Ou il n’ira pas voter. Ou bien il ira. Cela importe bien peu au final. Rien n’est mieux que rien, rien n’est plus beau que rien. Même « rien n’est mieux que rien » n’est pas mieux que « certaines choses sont mieux que d’autres ». C’est dire.

Ainsi, puisqu’il n’affirme rien, le sceptique radical ne se trompe jamais. À la bonne heure. Mais évidemment, en contrepartie, il se condamne à ne plus dire, à ne plus faire, autant dire à ne plus être. Ou à être tout juste une plante.

S’il [le sceptique] ne forme aucun jugement, ou plutôt si, indifféremment, il pense et ne pense pas en quoi différera-t-il des plantes ?

Aristote, Métaphysique⁴

Cela semble être une position bien peu satisfaisante.
Pourtant, la suspension du jugement, lorsqu’elle est appliquée temporairement, est une position épistémologiquement très saine, voire indispensable. Tant que je ne connais pas suffisamment un sujet, il est raisonnable de rester prudent, jusqu’à ce que la cumulation de connaissance me permette de trancher.

S’il veut prétendre être davantage qu’un cactus au soleil, le sceptique doit, tôt ou tard, faire le choix de dépendre son jugement qu’il avait soigneusement suspendu quelque temps.

“Certes, nous pouvons pour un moment déclarer que tout est égal, que la réalité n’est qu’un rêve. C’est très bien, cela nous fait sourire comme Bouddha ; mais ensuite, si nous choisissons de continuer à vivre dans la réalité, nous ne pouvons que nous remettre en jeu, comprendre et choisir. Nous pouvons se faisant continuer à sourire, mais nous ne continuons pas moins à nous mettre en jeu, à comprendre et décider.[…] Parce que juger et choisir est la même chose que penser et vivre”

Carlo Rovelli, Anaximandre ou la naissance de la pensée scientifique

Photo de Carlo Rovelli devant un tableau noir — Carlo Rovelli, physicien et philosophe des sciences, devant un tableau noir avec des équations (ça fait plus intelligent)

Cette position philosophique s’appelle scepticisme scientifique. On suspend prudemment son jugement (c’est la partie sceptique), jusqu’à ce que toute la puissance de la rigueur et de la démarche intellectuelle (c’est la partie scientifique) nous en libère. C’est ce que nous appellerons ici « dépendre son jugement ».

Mais donc une tension apparait : la vérité absolue nous est à jamais étrangère et pourtant il faut finir par trancher. Trancher ce qui est suffisamment fiable pour qu’on puisse le tenir pour vrai.
Et réfléchir à la manière dont on fait ce choix semble crucial pour avoir une démarche sceptique raisonnable.

La vérité au fond du puits (à gauche) et sortant du puits (à droite) deux tableaux de Jean-Léon Gérome. Le titre complet du second est « Vérité sortant du puits armée de son martinet pour châtier l’humanité ». Ça calme.

Quand faut-il « dépendre » son jugement ?

Considérons une affirmation A sur un sujet que je ne connais vraiment pas. Dans un premier temps, je n’exprime pas mon opinion sur le sujet. C’est ce que l’on appelle la suspension du jugement et c’est une position épistémologiquement saine (manière un peu pompeuse de dire « c’est pas con »).
Découvrant de mieux en mieux le sujet, j’accorde à l’affirmation A une vraisemblance croissante.
Mais à partir de quel degré de confiance en A, par rapport à non-A, est-il judicieux de commencer à exprimer mon opinion sur le sujet ? 51 % ? 75% ? 99% ? 100% ?
La réponse sceptique radicale serait 100% – autrement dit jamais – alors qu’une réponse assez crédule serait 51%.

Précisons, avant d’aller plus loin, que cela dépend fortement du contexte : je m’exprimerais avec plus ou moins de prudence suivant que ce soit au cours d’un repas de famille, d’une publication sur les réseaux ou d’un article scientifique. Mais ceci étant dit, cela ne change pas grand-chose à la suite de l’article.

Probablement que le plus judicieux est de naviguer quelque part entre ces deux positions. Mais pour trancher, il faut répondre à une question fondamentale : Qu’est-ce que l’on vise ?
Finalement, pourquoi sommes-nous sceptique, zététicien, ou penseur critique (selon votre terminologie préférée) ?⁵
L’importance de cette question était déjà identifiée par le philosophe David Hume :

Car voici la principale objection et la plus ruineuse qu’on puisse adresser au scepticisme outré⁶, qu’aucun bien durable n’en peut jamais résulter tant qu’il conserve sa pleine force et sa pleine vigueur. Il nous suffit de demander à un tel sceptique : Quelle est son intention ? Que se propose-t-il d’obtenir par toutes ces recherches curieuses ? Il est immédiatement embarrassé et ne sait que répondre.

Hume, Enquête sur l’entendement humain, cité dans Le scepticisme, Thomas Bénatouil

Hume reconnait par ailleurs la puissance des principes sceptiques. Selon lui, ceux-ci « fleurissent et triomphent dans les écoles où il est difficile, sinon impossible, de les réfuter ».
Il leur reproche en revanche leur inutilité quand ils sont employés dans leur « pleine force » : « Mais un pyrrhonien ne peut s’attendre à ce que sa philosophie ait une influence constante sur l’esprit, ou, s’il en a une, que son influence soit bienfaisante pour la société ».

Héritier de ce scepticisme, les zététiciens aujourd’hui ne tombent pas dans le piège de l’indifférence interminable des pyrrhoniens qui laissent pour toujours leurs jugements suspendus. Non, bien au contraire, les zététiciens, dépendent leur jugement : ils démystifient, ils enquêtent, ils trouvent, ils se positionnent, ils s’opposent, ils twittent, etc.
Ceci dit, cela ne devrait pas nous exempter de répondre à la question de Hume : Qu’est-ce que l’on vise en faisant cela ? Quelle règle permet de trancher si un niveau de connaissance est suffisant pour donner son avis ?

Ce qui est et qui doit être

Pour trancher sur ce qu’il faut faire, ou autrement dit, ce qui doit être, il peut-être utile de s’en remettre au principe de la guillotine de Hume⁷ que l’on pourrait formuler ainsi : « Ce qui doit être ne peut se déduire de ce qui est« .

Une proposition sur ce qui doit être, que l’on qualifiera de prescriptive (ou normative, éthique, morale, axiologique, politique selon les contextes) ne se déduit pas d’une proposition descriptive – sur ce qui est – mais d’une autre proposition prescriptive⁸.
Par exemple : la proposition prescriptive « L’homéopathie doit être déremboursée » ne peut se déduire ipso facto de la prémisse descriptive « L’homéopathie n’a pas d’effet propre ». Il faut y adjoindre une autre prémisse prescriptive comme « Ce qui est inefficace doit être déremboursée ». Dans ce cas, la démonstration est rigoureuse (ce qui ne signifie pas que la conclusion est vraie, mais que la véracité des prémisses implique la véracité de la conclusion).

Ainsi, pour savoir quand dépendre son jugement, inutile de contempler l’univers ou de charcuter des équations mathématiques. Ce n’est pas dans ce qui est que l’on trouvera une réponse. Il faut avant tout adopter une prémisse prescriptive. Il faut s’adosser à un système éthique, une règle (ou un ensemble de règles) axiomatique qui guident ce qu’il est éthique de faire ou de ne pas faire, ce que l’on considère comme bien et mal⁹.

En conjuguant des propositions prescriptives à des descriptions factuelles, il est alors possible de déduire de nouvelles affirmations prescriptives.

Illustration du principe de la guillotine de Hume

Ce prisme-là permet, d’ailleurs, de justifier la position des sceptiques pyrrhoniens. Leur objectif primordial est d’atteindre l’ataraxie, c’est-à-dire l’absence de trouble. Voilà donc leur prémisse prescriptive.
D’autre part, ils développent un argumentaire qui ressemble à cela : La suspension du jugement (épochè), engendre l’absence de jugement (adoxastous) qui engendre l’absence d’affirmation (aphasie). Enfin, puisque ne rien affirmer épargne les déceptions, erreurs et faux espoirs, il s’ensuit l’absence de trouble (ataraxie). ¹⁰.
Conclusion implacable : Il faut toujours suspendre son jugement.

Guillotine de Hume appliquée au pyrrhonisme

Il est évidemment possible de discuter de cette construction argumentaire en prenant soin de traiter les propositions descriptives et prescriptives en tant que telles. Il n’y a pas de sens à dire que la recherche de l’ataraxie est vraie ou fausse, comme il n’y a pas de sens à dire que le fait que l’aphasie implique l’ataraxie soit bien ou mal.

« Le sceptique, parce qu’il aime les hommes… »

La construction précédente n’est qu’une interprétation du scepticisme pyrrhonien – peut-être un peu naïve – qui ne rend pas entièrement hommage à cette pensée complexe qui ne se laisserait pas si simplement capturée dans un cadre aussi rigide.
Voyons maintenant, une autre interprétation du pyrrhonisme, qui permet également d’illustrer le principe de la guillotine de Hume. Elle se fonde sur cet extrait de Sextus Empiricus :

Le sceptique, parce qu’il aime les hommes , veut les guérir par le discours autant qu’il le peut, de la témérité et de la présomption dogmatique.

Sextus Empiricus , Esquisses Pyrrhoniennes

D’après ce passage, le principe prescriptif fondateur du scepticisme serait l' »amour des humains » ou autrement la défense des individus¹¹ . En le conjuguant à une proposition descriptive implicite ici (quelque chose comme « La présomption dogmatique nuit aux humains »), on en déduit qu’il faut lutter contre la présomption dogmatique.

Interpertation de Sextus Empiricus du point de vue de la guillotine de Hume — Interprétation de Sextus Empiricus du point de vue de la guillotine de Hume

Petite parenthèse : ce passage semble mettre à jour un paradoxe entre deux justifications du scepticisme. D’une part la recherche de l’ataraxie, qui justifie de suspendre éternellement son jugement, d’autre part un engagement « humaniste » qui, semble-t-il, peine à justifier cette incessante aphasie (Si « le sceptique aime les hommes » doit-il suspendre son jugement devant les pires des injustices ?).
Une réponse à ce paradoxe est peut-être donnée un peu plus loin dans le texte de Sextus Empiricus dans un paragraphe intitulé « Pourquoi le sceptique s’applique-t-il parfois à proposer des arguments d’une faible valeur persuasive ? »

[Le sceptique] use d’argument de poids propres à venir à bout de cette maladie qu’est la présomption dogmatique pour ceux qui sont fortement atteints de témérité, mais il use de plus léger pour ceux qui sont superficiellement atteints par le mal de la présomption et facile à soigner et qu’il est possible de rétablir par une persuasion plus légère.

Sextus Empiricus, Esquisses Pyrrhonienne

Ce point de vue pourrait expliquer la position extrême des sceptiques de l’antiquité : en réalité, la force de leur discours s’adapte en fonction de leur interlocuteur et ce seraient les arguments les plus radicaux qui auraient été retenus par l’histoire.
Peut-être alors que le vrai projet pyrrhonien n’était pas tant de défendre un doute absolu et inconditionnel, presque insensé, mais plutôt de protéger les hommes des discours dogmatiques et la tradition n’aura retenu que les positions les plus radicales qu’ils tenaient face à leurs adversaires les plus coriaces. Peut-être.

Refermons cette parenthèse antique qui permettait surtout d’illustrer différentes constructions argumentaires qui aboutissent à différents projets sceptiques : suivant la prémisse prescriptive qui fonde le discours, les conclusions peuvent différer. Elle influence donc notre rapport à la suspension du jugement, mais pas seulement. Elle guide également le choix des sujets que l’on va traiter, le ton que l’on va adopter, l’audience à qui l’on veut diffuser ces idées, etc.

Prenons un exemple.
Considérons les deux propositions descriptives suivantes : « X prétend être atteint de la pathologie P »; « Il est très probable que X ne soit pas vraiment atteint de la pathologie P ». Doit-on, face à une telle situation, suspendre son jugement sur ce qui est vrai ou faux et sur ce qui est bien ou mal de faire ?
La réponse dépend de la prémisse prescriptive ; par exemple : « Il faut maximiser le bonheur de X », « Il faut dévoiler coute que coute la vérité sur P », « Il faut informer au mieux sur P sans nuire à X », etc.

Posture morale par défaut

Est-il possible d’échapper au choix ?

Non seulement le sceptique doit choisir. Mais pire, il le fait. Aussi attaché soit-il à la suspension du jugement, un sceptique finira tôt ou tard par choisir. La prétention à une indifférence absolue ne survit guère en dehors du confort d’un cabinet de philosophe. Elle s’évapore à l’instant où l’on quitte ces élégantes constructions mentales.

« Comme le doute sceptique résulte naturellement d’une réflexion profonde et intense […], il augmente toujours à mesure que nous poursuivons nos réflexions, qu’elles s’opposent à lui où lui soit conformes. Seules la négligence et l’inattention peuvent nous apporter quelques remèdes.
C’est pourquoi je leur fais entière confiance et j’admets sans discussion que, quelle que soit l’opinion du lecteur à cet instant, il sera dans une heure persuadé qu’il existe à la fois un monde extérieur et un monde interne ».

David Hume, Traité de la nature humaine, I,IV, II

Ainsi, impossible de se croire exempté de la laborieuse tâche qui consiste à s’interroger sur le fondement de son entreprise sceptique.
Que ce soit réfléchi ou non, toute démarche sceptique (et intellectuelle plus généralement) s’appuie sur des hypothèses sous-jacentes sur ce qui doit être.
La vérité est au fond du puits. Qu’est ce qui me donne suffisamment soif pour m’y pencher ?

Quelles valeurs par défaut ?

On pourrait alors réfléchir, à ce qui guide inconsciemment les choix moraux, aux prémisses prescriptives que l’on applique par défaut sans en avoir conscience. On prendrait alors le risque de sortir du champ de cet article (et de mes compétences) alors que d’autres l’ont déjà fait très bien (ici par exemple, ou plus récemment là).
Simplement, il semble que l’on peut remonter à quelques invariants dans notre manière de faire des choix inconscients parmi lesquels la consistance avec son groupe social. Qu’on l’appelle conformisme à la façon de Asch, ou capital symbolique à la manière de Bourdieu, notre conception du monde, et à fortiori notre conception du bien, s’aligne souvent sur la conception que s’en font nos semblables.

Beaucoup de nos actions sont mises en œuvre, non pas pour ce qu’elles sont, mais pour acheter le regard de l’autre.

Aurélien Barrau, extrait de conférence samplé dans Nouveau Monde de Rone.

Évidemment, les milieux sceptiques ne sont pas épargnés par ce mécanisme et certains comportements ou prises de position sont motivés, au moins partiellement, non pas par leur valeur épistémique intrinsèque ou leur bénéfice espéré, mais par ce qu’elles sont valorisées par la communauté.
Que ce soit dans le choix des sujets, dans le ton adopté, dans l’audience visée. Ainsi, semblent apparaitre certaines valeurs qui s’éloignent de la démarche sceptique et humaniste défendue il y a 2000 ans déjà par Sextus Empiricus : le sceptique, parce qu’il aime les hommes…

Application : Zététique et psychophobie.

Certains discours reprochent à la zététique d’être psychophobe notamment en ce qu’elle utiliserait à tort le champ lexical de la psychiatrie et/ou banaliserait des termes péjoratifs sur la santé mentale (fou/folle, démence, parano, perché, …). Une synthèse de cette critique peut être retrouvé dans l’article « Zététique & Psychophobie » de Sohan Tricoire.
D’autres voix se sont élevées contre cette critique parce qu’elle leur paraissait infondées, moralisatrice ou inutilement tatillonne.

Du haut de mon ignorance, difficile d’avoir un avis péremptoire sur la question :
Quel est l’impact réel de l’utilisation de ces termes ? Est-ce que le fait de décrire ces termes comme violents ne contribue-t-il pas, justement, à les faire ressentir comme violents ? Cette critique procède-t-elle, comme on peut l’entendre, d’une pureté militante propre à la culture « woke » ?
D’un autre coté, les personnes qui s’opposent à cette critique ne sont-elle pas, simplement sur la défensive face à un discours qui remet en cause leurs habitudes et qui les accuse d’une certaine violence ?
Est-ce que je peux, moi, remettre en question la violence ressentie par d’autres ? Et d’ailleurs, n’étant pas concerné, est-il judicieux que je m’exprime sur cette question ?

Toutes ces questions demandent des connaissances en linguistique, en psychologie, en sociologie, en philosophie voire en politique, que je n’ai absolument pas. De ce fait, comment me positionner face à cette question ?

Si, à la manière de Sextus, on adopte la défense des individus comme objectif premier, il en découle (assez naturellement) que la défense des individus marginalisés ou soumis à des oppressions, est d’autant plus important.
Ainsi, face aux doutes que je peux avoir, mon raisonnement revient à cet objectif premier et, dans certains contextes au moins, il me semble plus important de défendre la voix des oppréssé.e.s que de laisser mon jugement suspendu.

Il me semble que personne (ou peu) refuserait consciemment la posture « humaniste » proposée ici et déciderait à la place d’adopter un autre objectif comme le triomphe coute que coute de la vérité.
En réalité, ce qui empêche certaines personnes d’adopter cette position « humaniste » relève davantage d’un aveuglement par rapport à leur valeur morale implicite qui risque de se retrouver de facto calqué sur une idéologie dominante. Ce qui ramène à l’importance cette question déjà posée plus haut : « Qu’est ce que l’on vise ? »

Une partie de l'excellente équipe de la médiathèque d'Aubagne et des services jeunesse et prévention

Ateliers Esprit critique et autodéfense intellectuelle

17 juin 202121 juin 2021 Denis Caroti

Une partie de l'excellent équipe de la médiathèque d'Aubagne

Depuis 2019, le Cortecs travaille avec la médiathèque d’Aubagne et les services jeunesse et prévention de la Mairie d’Aubagne pour élaborer et construire des ateliers sur la thématique de l’esprit critique et de l’autodéfense intellectuelle à destination des élèves des collèges et lycées de l’académie d’Aix-Marseille. Après plusieurs journées de formations, les animateurs sont intervenus régulièrement auprès des classes sur différentes thématiques. Ce travail a permis de repenser, actualiser, mais aussi de créer des ateliers permettant d’aborder des « classiques » de la zététique : effet Barnum, principe de parcimonie, échelle des preuves ou coïncidences, autant de sujets que les élèves ont pu découvrir grâce à toute l’équipe qui partage aujourd’hui ses productions et ressources avec nous. Un grand merci et surtout bravo à eux pour tout cela !

Table of Contents

Présentation du projet

Objectifs, compétences travaillées, organisation des séances : ce document présente le projet dans son ensemble.

Description des ateliers

Vous trouverez ci-dessous les différents ateliers proposés ainsi que tous les contenus utilisés et que toute l’équipe partage avec plaisir. Le dossier complet est ici. Merci à eux !

Jouer à débattre

Jouer à débattre (atelier créé par L’arbre des connaissances). Le thème choisi a été l’humain augmenté. Le but étant d’amener les élèves à argumenter et à prendre conscience de la complexité insoupçonnée des sujets de société.

Atelier philo

S’exercer à réfléchir, apprendre à discuter, écouter, raisonner et respecter l’autre avec cet atelier philo.

Fake news

Cet atelier correspond à l’atelier « Le vrai du faux » (créé par le CRIJ). L’objectif est d’appréhender la complexité à évaluer la fiabilité des informations et de se poser les bonnes questions pour y parvenir.

Test de personnalité : l’effet Barnum

Un « classique » de la zététique où l’on va reproduire l’expérience de Bertram Forer sur l’effet qui porte son nom (mais aussi celui d’effet Barnum) : un atelier mettant en scène un faux test de personnalité à évaluer par les élèves. Vous retrouverez dans ce dossier les fiches, vidéos et autres documents utilisées pour mener à bien cet atelier.

Principe de parcimonie et rasoir d’Occam

Comment travailler sur le principe de parcimonie avec les élèves ? Comment faire découvrir cet outil de tri des hypothèses et ses limites ? Le dossier avec tous les éléments se trouve ici !

Échelle des preuves et curseur de confiance

Un atelier repris de l’activité proposée dans l’excellent ouvrage publié par nos collègues de La main à la pâte, et qui permet de travailler avec les élèves sur la notion de preuves et de confiance. Tout le dossier est à retrouver ici.

Coïncidences…

Un atelier sur la notion de coïncidences : y a-t-il forcément un sens à donner à ces conjonctions d’événements intrigants et qui nous paraissent si étranges…? Le dossier complet ici !

Bilan

Voici quelques retours concernant les ateliers

Au niveau de l’enchainement des ateliers, commencer par Jouer à débattre permet de créer une bonne relation avec les élèves qui se retrouvent dans une situation de jeu qui les change de leur quotidien. L’atelier sur les fake news comme les suivants sont un peu plus scolaires, contenant plus d’explications (un peu plus descendant) : les élèves sont mis en activité, mais cela demande toujours une implication de leur part qui dépend bien entendu de beaucoup de paramètres.

On a pu remarquer que les ateliers Jouer à débattre, effet Barnum et rasoir d’Occam ont très bien fonctionné : le mélange entre travail de groupe, débat et effet de surprise motive toujours les élèves et retient leur attention.

Concernant l’atelier sur l’effet Barnum, il faut bien penser à faire attention aux contacts possibles entre élèves pour éviter qu’ils comprennent le truc.

L’atelier sur l’échelle des preuves est aussi à améliorer sur la manière de l’animer : nous proposons d’y ajouter davantage de moments d’interactions variées.

Loïc Massaïa, imperturbable mais toujours pertinent !

Un merci très spécial à Loïc Massaïa pour le soutien, l’expertise et l’aide apportée tout au long de ces ateliers, mais également pour le partage des documents !

Scepticothèque : films et esprit critique

2 décembre 20202 décembre 2020 Denis Caroti

Voilà plusieurs mois que Vivien Soldé, doctorant en sociologie à l’Université de Reims Champagne-Ardenne, nous a parlé de sa « scepticothèque : la cinémathèque sceptique et zététique » regroupant des œuvres cinématographiques en lien avec l’esprit critique, le scepticisme, l’autodéfense intellectuelle. C’est un travail précieux que nous partageons aujourd’hui car il regroupe et permet de (re)découvrir des films parfois anciens, mais dont l’objet interroge des thématiques que nous avons l’habitude de rencontrer dans notre vie de sceptiques… Du Procès du singe en passant par Contact, Yéti et compagnie, ou encore Experimenter, l’ensemble de ces œuvres peut aussi constituer un vivier pertinent de ressources pédagogiques, à exploiter avec élèves et étudiants, pour travailler sur les thématiques abordées.
Cerise sur le gâteau, Vivien a également concocté une sélection de 10 films pour le confinement (celui de mars-avril est ici), à déguster entre deux apéros à distance…
Merci et encore bravo à lui pour tout ce travail !

La scepticothèque est à découvrir ici

10 films « sceptiques » pour le confinement (1) à regarder entre deux apéros à distance : c’est là

10 filmes « sceptiques » pour le confinement (2) à regarder entre deux apéros à distance : c’est là

L’effet Matilda ou l’invisibilisation des femmes de science

2 décembre 20202 décembre 2020 Clara Egger

En pensée critique, on connaisait l’effet Mathieu ⁵ faisant référence à la moindre recognition (notamment en science) de ceux qui parte avec un capital de départ (matériel, social ou culturel) moins élévé. On doit à Margaret Rossiter, historienne des sciences états-unienne, une variante, l’effet Matilda, un clin d’oeil à la suffragiste, libre-penseuse, abolitionniste, Matilda J. Cage, une des premières à dénoncer l’absence des femmes dans les récits historiques et scientifiques.

Parmi les sans-droits et sans-noms des oubliettes de l’histoire des sciences, une écrasante majorité a en commun d’être de genre féminin. Les femmes scientifiques sont moins reconnues de leur vivant, notamment en raison de leur statut plus précaire et subordonné. ⁶ Leur contribution est aussi invisibilisée dans les récits scientifiques, par paresse – on s’attarde uniquement sur les figures, principalement masculines, déjà connues -, inertie ou biais sexiste.

Margaret W. Rossiter revient sur certaines de ces figures oubliées dans son article sur l’effet Matilda ¹⁸. Une des premières connues est Trota, une médecin de l’Italie du douzième siècle, qui documenta et traita, de manière inédite, des pathologies féminines. Son nom devint connu par l’action de son époux et de son fils, tous deux médecins également. Un moine, chargé de rédiger un traité sur la médecine au Moyen-Age, décida toutefois qu’une telle contribution ne pouvait être que le fait d’un homme et donna à son nom la forme latine masculine. Une erreur qui la fit passer, en tant qu’homme, à la prospérité. Il faudra attendre le vingtième siècle pour que cette erreur soit réctifiée par l’historien de la médecine allemand Karl Sudhoff, qui, au passage, dégrada sa qualification au rang d’assistante sage-femme, un statut qui retira toute mention à ses découvertes dans les ouvrages scientifiques postérieurs.

Trota – aussi appelée Trotula – représentée dans une gravure du quatorzième siècle.

Plus proche de nous, Frieda S. Robscheit-Robbins, doctoresse en médecine allemande experte du traitement de l’anémie, fut privée du Prix Nobel en 1934 au profit de son co-auteur. L’histoire retient par contre, sa « présence »et ses coiffes toujours élégantes ¹⁹. Si les femmes non- mariées sont d’office non reconnues, les travaux et découvertes des femmes mariées à d’autres scientifiques reviennent, quasi systématiquement, à leur conjoint, même dans les cas, nombreux, où leur contribution excède celle de leur partenaire masculin.

En qualifiant cette stratégie d’invisibilisation systématique, l’effet Matilda invite à accroître notre vigilance et à considérer, au moment de se pencher sur l’histoire des découvertes scientifiques, qu’il est fort probable que derrière chaque grand homme se cache non seulement une multitude de collaborateurs oubliés mais aussi un grand nombre de femmes.

Si vous faites partie de celles et ceux qui ont contribué à réparer cette injustice en effectuant des recherches sur des femmes scientifiques oubliées? Contactez nous !

Vers une vision bayésienne de la zététique: Justifier et enrichir la démarche zététique à partir de la formule de Bayes

17 septembre 202011 octobre 2021 Alexandre Changenet et Nicolas Martin

Nicolas Martin, après avoir étudié les mathématiques appliquées à l’INSA Toulouse, a obtenu son doctorat en automatique au sein du GIPSA-lab et de l’université Grenoble Alpes. Il s’intéresse depuis plusieurs années à la zététique, l’esprit critique et leur transmission auprès du public. Depuis début 2020, Il publie des articles de vulgarisation scientifique et d’esprit critique sur le blog « Mon Œil ! »²⁰Voici une de ses productions:

La zététique est un mouvement de pensée qui promeut l’utilisation de la pensée critique et de la méthode scientifique pour traiter efficacement le tsunami d’informations qui nous parvient chaque jour. Il semble néanmoins que cette démarche serait plus efficace encore si elle était soutenue par une vision bayésienne c’est-à-dire une approche qui prône l’usage des probabilités pour quantifier nos croyances. La démarche zététique est régulièrement le fruit de critiques : elle parait parfois dogmatique, parfois antipathique et parfois inapte à répondre à certains problèmes. Nous verrons dans cet article que le raisonnement bayésien soutient l’approche zététique et lui apporte un peu de nuance. Récemment, plusieurs travaux dans la communauté zététique sont allé dans ce sens, initiés principalement par Lê Nguyen Hoang (influencé par les travaux de Julia Galief écrivaine, conférencière et co-fondatrice du Center for Applied Rationality), avec son livre « La formule du savoir », sa série de vidéos sur le sujet ²¹ et ses podcasts²², l’approche bayésienne et ses apports à la zététique ont également été traités par Christophe Michel (animateur de la chaine Hygiène mentale)²³, Nathan Uyttendaele (animateur de la chaine Chat Sceptique)²⁴ ou encore Thibaud Giraud (animateur de la chaine Monsieur Phi)²⁵. C’est dans ce mouvement que s’inscrit cet article dont l’objectif principal est de montrer comment le bayésianisme corrobore et enrichit certains outils zététiques.
Nous présenterons dans un premier temps quelques points critiques de la zététique qui motivent l’introduction d’un cadre bayésien. Nous introduirons ensuite succinctement le formalisme bayésien avant de présenter dans la dernière partie la contribution principale de cet article : la déduction de deux principes zététiques, rasoir d’Ockham et maxime de Hume, à partir de la formule de Bayes, formule sur laquelle se base l’approche bayésienne.
Cet article est loin de faire le tour de la question. Au contraire, comme son titre l’indique, le but ici est de fournir quelques arguments invitant à une réflexion plus poussée sur l’apport de l’approche bayésienne à la zététique.

Les limites de l’approche zététique

Il semble que l’approche zététique ait une mauvaise image de la part des croyant-e-s et des tenant-e-s des affirmations para-scientifiques²⁶ mais pas seulement, certaines critiques viennent des zététiciens eux-mêmes²⁷. Si certaines critiques peuvent être maladroites, d’autres en revanche nous paraissent pertinentes. Notons également que la plupart des critiques ne concerne pas la zététique dans son essence mais des écueils dans lesquelles il est facile de tomber. Nous proposons une liste de ces critiques ci-dessous. Nous verrons ensuite en quoi le bayésianisme peut répondre en partie à ces défaillances.

Des principes dogmatiques

Le rasoir d’Ockham, la maxime de Hume, la charge de la preuve, la valeur d’une preuve, l’impossibilité de prouver l’inexistence… Ces principes se posent parfois comme des dogmes de la zététique. Ce n’est pas un problème en soi puisque leur justification apparaît a posteriori : On se rend compte, en les utilisant, qu’effectivement on a tendance à se tromper moins souvent. En revanche, justifier a priori que ces principes sont cohérents, sont suffisants et nécessaires est une question plus complexe mais qui soutiendrait d’autant plus la démarche zététique.
En réalité, nous le verrons plus loin: le rasoir d’Ockham et la maxime de Hume peuvent se déduire de la formule de Bayes, formule dont on peut également justifier la cohérence.

De bons outils dans des mains maladroites

Carl Sagan dans The Fine art of Baloney Detection accompagne son texte de cette note appelant à la précaution : Like all tools, the baloney detection kit can be misused, applied out of context, or even employed as a rote alternative to thinking. But applied judiciously, it can make all the difference in the world — not least in evaluating our own arguments before we present them to others²⁸. De même, dans son article critiquant la zététique, Sylvain Poirier fait remarquer : Ce n’est pas parce que beaucoup de principes zététiques affichés sont bons, que tout ce que disent les zététiciens est à croire sur parole. Si la zététique apporte un panel d’outils finement aiguisés, ils peuvent parfois être délétères lorsqu’ils sont utilisés sans un peu d’esprit critique.

Manque d’un formalisme mathématique

Le rasoir d’Ockham nous invite à “Privilégier l’hypothèse la plus parcimonieuse”. Mais comment quantifier la parcimonie d’une hypothèse ? Quelle métrique utiliser ?
La maxime de Hume, elle, stipule que “Une affirmation extraordinaire requiert des preuves extraordinaires”. Mais comment quantifier cette extraordinarité ? Et comment comparer l’extraordinarité d’une affirmation et l’extraordinarité des preuves ?
Bonne nouvelle, même si ces préceptes font office de principes généraux sans prétendre avoir une quelconque valeur quantitative, ils peuvent en fait être déduit de la formule de Bayes. Qui plus est, cette dernière leur donne un sens mathématique.

Manichéisme des arguments

Le curseur de vraisemblance²⁹ invite à graduer la vraisemblance d’une affirmation sur une échelle continue entre 0% et 100%. Cette précaution apportée à notre jugement sur une théorie est bénéfique mais elle disparaît souvent quant on juge les preuves qui soutiennent la théorie : Il n’est pas rare d’entendre que tel argument est soit valide soit invalide; que le manque de rigueur d’un protocole invalide les résultats d’une expérience; que l’on peut jeter un discours puisque l’on y relève l’argument fallacieux n^∘21 ou le n^∘37³⁰. Il semble cependant que l’on perde de l’information en disqualifiant complètement une preuve imparfaite³¹. Dans son article critiquant la zététique, Sylvain Poirier écrit: Le fait qu’il y ait des impostures et des erreurs de toutes sortes à la base de certaines affirmations du paranormal ou d’autres choses par les uns ou les autres, ne signifie pas que tout y est faux ni que rien n’aurait pu être effectivement prouvé. Est-il bien raisonnable de considérer la valeur d’un argument comme binaire ? Il semble peu probable qu’un protocole soit parfait tout comme il est peu probable que tout soit à jeter. En replaçant la zététique dans un cadre probabiliste, on quitte le maigre³² {0;1} pour l’infiniment plus riche³³ [0,1].

Difficulté de conclure

“Est-il préférable pour la guérison d’une entorse de dormir avec un coussin bleu ou avec un coussin rouge ?”. Face à l’inexistence d’expériences randomisées en double aveugle avec groupe de contrôle, le zététicien doit-il s’enfuir laissant là son jugement suspendu ?
Devant bien des affirmations il semble que les outils de la zététique ne permettent pas de conclure. En particulier, on évoque souvent la hiérarchie suivante : une étude isolée est moins pertinente qu’une méta-analyse et une méta-analyse est moins pertinente que le consensus scientifique³⁴. Mais alors, que dire d’un sujet sur pour lequel il existe peu ou pas d’étude ? Que dire d’un sujet face à un faisceau d’indices réduit et/ou peu rigoureux ? L’approche bayésienne permet de prendre en compte des informations de toutes sortes afin de se faire une opinion.

Et donc ?

L’approche bayésienne offre une perspective qui répond en partie aux critiques sus-citées en permettant de :

Quantifier la validité d’une information et la probabilité d’une affirmation.
Corroborer certains des principes dogmatiques de la zététique évoqués ci-dessus
Replacer le discours zététique dans un langage probabiliste : Utiliser une formule comme « Il est très improbable que X » plutôt qu’un plus catégorique « À l’heure actuelle, il n’y a aucune preuve de X » rend le discours plus humble et plus propice à un échange bienveillant³⁵.

Les apports du bayésianisme

Pour ne pas alourdir l’article la présentation du bayésianisme est assez minimaliste. Le lecteur curieux est invité à se référer aux références données dans l’introduction.

De la formule de Bayes

Le bayésianisme se base sur la formule de Bayes dont il tire son nom. La manière la plus simple d’écrire cette formule est la suivante

(1) $\begin{equation*}\Prob{A|B} = \frac{\Prob{A}\Prob{B|A}}{\Prob{B}}\end{equation*}$

Les termes ℙ(A|B) et ℙ(B|A) sont des probabilités conditionnelles et se lisent respectivement “Probabilité de A sachant B” et “Probabilité de B sachant A”. La formule de Bayes permet donc simplement de lier les deux probabilités conditionnelles.

Exemple : On considère un lancer de dé, et on cherche à savoir quelle est la probabilité que le dé soit tombé sur 6 sachant que le dé est tombé sur un chiffre pair. On parle donc de probabilité conditionnelle car on cherche la probabilité d’un évènement en connaissant des informations partielles sur cet évènement.
Dans la formule de Bayes 1, on remplace A et B respectivement par “Faire un 6” et “Faire un nombre pair”. On va donc pouvoir calculer ℙ(A|B), la probabilité de “Faire un 6” sachant qu’on a “Fait un nombre pair”, ce qui est bien ce qu’on recherche. On obtient :

$\small \Prob{\text{Faire un 6}|\text{Faire un nombre pair}} = \frac{\Prob{\text{Faire un 6}}\Prob{\text{Faire un nombre pair}|\text{Faire un 6}}}{\Prob{\text{Faire un nombre pair}}}$

Ce qui se lit : la probabilité que j’ai fait un 6 sachant que j’ai fait un nombre pair est égale à la probabilité de faire un 6 (égale à 1/6) multipliée par la probabilité de faire un nombre pair sachant que j’ai fait un 6 (égale à 1) divisée par la probabilité de faire un nombre pair (égale à 1/2). Ce qui donne :

$\begin{equation*} \Prob{\text{Faire un 6}|\text{Faire un nombre pair}} = \frac{1/6 \times 1}{1/2} = 1/3 \end{equation*}$

que l’on peut facilement vérifier.

À la formule du savoir

Initialement cette formule est un simple outil de calcul de probabilité conditionnelle relativement simple, et c’est ainsi qu’elle est enseignée aux étudiants. Cependant, réinterprétée, notamment par Pierre-Simon de Laplace, elle est devenue un profond principe épistémologique, que certains considèrent comme la formule ultime du savoir³⁶ fondant ainsi le bayésianisme.
Comme nous le verrons, la formule de Bayes permet de calculer la vraisemblance d’une affirmation en fonction de la vraisemblance a priori de cette affirmation et d’une nouvelle information. Autrement dit, elle permet de mettre à jour nos croyances en fonction des preuves que l’on peut rencontrer : témoignage, étude scientifique, reportage TV, article de presse, …
Le théorème dit de Cox-Jaynes permet même de s’assurer que c’est la bonne manière de faire. Ce théorème montre que la logique bayésienne découle de certains prérequis naturels³⁷ et qu’elle est donc indispensable pour manipuler raisonnablement de l’information.

La théorie des probabilités n’est rien d’autre que le sens commun qui fait calcul — Pierre-Simon de Laplace

Retour à la zététique

Nous voilà rendus bien loin des préoccupations zététiques. Mais en apportant une légère modification à la formule de Bayes ci-dessus nous allons y revenir. Changeons tout simplement le A dans la formule par affirmation, et le B par preuve³⁸. Et voilà, nous avons un outil mathématique puissant pour estimer la vraisemblance d’une affirmation à partir de preuves (que ce soit des témoignages, des études, des arguments, …).
Mise en pratique :

$\begin{equation*} \Prob{\text{Affirmation}|\text{Preuve}} = \frac{\Prob{\text{Affirmation}}\Prob{\text{Preuve}|\text{Affirmation}}}{\Prob{\text{Preuve}}} \end{equation*}$

$\Prob{\text{Affirmation}|\text{Preuve}}$ est ce que l’on cherche à évaluer: la vraisemblance d’une affirmation à partir de preuves. Plus précisément, on cherche à calculer l’évolution de la confiance à accorder en une affirmation lorsque une nouvelle preuve est disponible. Cette quantité est aussi appelée probabilité a posteriori puisqu’elle correspond à la vraisemblance de l’affirmation après avoir pris en compte la preuve.
Par opposition, $\Prob{\text{Affirmation}}$ représente la probabilité a priori. C’est à dire la vraisemblance de l’affirmation avant de prendre en compte la preuve. C’est un des principes fondamentaux du bayésianisme : notre croyance en une affirmation évolue sans cesse en fonction des nouvelles preuves qui nous parviennent.
$\Prob{\text{Preuve}}$ est la probabilité a priori d’observer la preuve. Insistons: ces deux dernières probabilités ( $\Prob{\text{Affirmation}}$ et $\Prob{\text{Preuve}}$ ) sont calculées dans l’état initial des connaissances, c’est-à-dire sans prendre en compte la nouvelle preuve.
Enfin, la formule de Bayes nous dit que pour trouver $\Prob{\text{Affirmation}|\text{Preuve}}$ , il nous faut, de plus, la probabilité d’observer cette preuve si l’affirmation est vraie. Cette probabilité est notée: $\Prob{\text{Preuve}|\text{Affirmation}}$ , et est également appelée « fonction de vraisemblance », ou simplement « vraisemblance ».
On peut alors calculer $\Prob{\text{Affirmation}|\text{Preuve}}$ , la probabilité a posteriori de l’affirmation, c’est-à-dire la confiance à accorder en l’affirmation³⁹ une fois pris en compte les nouveaux éléments de preuve relativement aux connaissances préalables. D’une certaine manière, la formule décrit comment utiliser raisonnablement le curseur de vraisemblance connu des zététiciens.
La dépendance aux connaissances initiales peut sembler gênante puisqu’elle est subjective et risque de faire aboutir deux personnes à des conclusions différentes. Cependant la formule de Bayes assure qu’avec un nombre de preuves suffisant les probabilités a posteriori convergent vers une même valeur quelque soit la probabilité a priori.
Avec ces notations, une affirmation est très probable si $\Prob{\text{Affirmation}}$ est proche de 1 et inversement très improbable si $\Prob{\text{Affirmation}}$ est proche de 0. De même, $\Prob{\text{Preuve}}$ proche de 0 correspond à une preuve très improbable dans le cadre initial de nos connaissance donc à une preuve que l’on peut qualifier d’extraordinaire (par ex. « Il a neigé en Août »), alors que $\Prob{\text{Preuve}}$ proche de 1 est une preuve banale c’est à dire une information à laquelle on s’attend (par ex. « Il a neigé en Janvier »).
Avant de voir les avantages du cadre bayésien dans la démarche zététique, voyons un exemple rapide d’utilisation de la formule de Bayes dans un cadre zététique.

Exemple : La maison de mes grand-parents est connue pour être hantée, notamment la vieille chambre du fond. Armé de tout mon courage et de mes solides outils zététique je vais la visiter. J’émets deux hypothèses :

Affirmation Affirmation $A_1$ : « Il y a des oiseaux dans les combles à l’origine des phénomènes ». J’y attribue une probabilité de $\Prob{A_1} = 0.9$ .
Affirmation $A_2$ : « Il n’y a pas d’oiseau dans les combles et la maison est vraiment hantée ». J’y attribue une probabilité $\Prob{A_2} = 0.1$ ça paraît fou mais la croyance est tenace dans la famille et dans le village.

En arrivant dans la chambre, et non loin en dessous d’une ouverture dans le plafond qui donne accès aux combles, je vois une plume d’oiseau. Voilà ma nouvelle preuve $P$ qui va me permettre de mettre à jour mes croyances. On peut estimer la probabilité de trouver une plume là sachant qu’il y a des oiseaux dans les combles $\Prob{P|A_1} = 0.05$ : c’est commun de trouver des plumes mais encore fallait il qu’elle passe par cette petite ouverture. De même on estime la probabilité de trouver une plume sachant qu’il n’y a pas d’oiseau $\Prob{P|A_2} = 0.0001$ : c’est très peu probable, il aurait fallu que quelqu’un l’amène ici. On peut enfin calculer la probabilité de trouver une plume $\Prob{P}$ grâce à la formule suivante⁴⁰: $\Prob{P} = \Prob{P|A_1}\times\Prob{A_1} + \Prob{P|A_2}\times\Prob{A_2} = 0.04501$ .
On peut maintenant appliquer la formule de bayes pour $A_1$ et $A_2$ .

$\begin{equation*} \begin{split} \Prob{A_1 | P}& = \frac{\Prob{A_1}\Prob{P|A_1}}{\Prob{P}}\\ \Prob{A_1 | P} & = \frac{0.9 \times 0.05}{0.04501}\\ \Prob{A_1 | P} & \approx 0.9998 \end{split} \end{equation*}$

$\begin{equation*} \begin{split} \Prob{A_2 | P} & = \frac{\Prob{A_2}\Prob{P|A_2}}{\Prob{P}}\\ \Prob{A_2 | P} & = \frac{0.1 \times 0.0001}{0.04501}\\ \Prob{A_2 | P} & \approx 0.0002 \end{split} \end{equation*}$

Après mise à jour des vraisemblances j’attribue donc une probabilité de $99,98\%$ pour l’affirmation $A_1$ et $0,02\%$ pour l’affirmation $A_2$ .
Évidemment faire une telle analyse chiffrée n’est pas possible au quotidien et ce n’est même pas utile à vrai dire. Mais il est très bénéfique d’adopter une pensée bayésienne en prenant l’habitude de mettre à jour la vraisemblance de nos croyances et en musclant notre intuition bayésienne⁴¹.

On peut maintenant voir en quoi cette approche permet de répondre aux critiques formulées dans la section précédente :

Elle peut être utilisée pour justifier les principes a priori arbitraires de la zététique. Puisque le théorème de Cox-Jaynes montre que l’approche bayésienne est la seule cohérente, alors démontrer les principes zététiques par la formule de Bayes justifierait leur pertinence. C’est ce que nous ferons dans la dernière section pour deux de ces principes.
Puisque dans l’approche bayésienne tout est exprimé en fonction de probabilité on évite la binarité et la rigidité que peut prendre parfois le discours zététique.
Comme nous le verrons dans la dernière section, en plus de justifier le rasoir d’Ockham et la maxime de Hume, l’approche bayésienne apporte un cadre mathématique qui permet de quantifier ce qu’on entend par « l’hypothèse la plus parcimonieuse » ou une « affirmation extraordinaire ».
Alors que la zététique requiert parfois une étude approfondie d’un sujet pour obtenir une conclusion, l’approche bayésienne permet toujours d’attribuer une vraisemblance à l’affirmation quel que soit la quantité d’information dont on dispose.

Les outils zététiques dans une main bayésienne

Les deux premières parties ont permis de montrer ce que le bayésianisme peut apporter à la zététique et s’alignent avec des travaux pré-existants (notamment ceux de Christophe Michel présenté dans l’introduction). Cette dernière partie est une contribution plus personnelle (et plus technique aussi peut-être) et montre comment le cadre bayésien permet de justifier deux principes fondamentaux de la zététique : le rasoir d’Ockham et la maxime de Hume répondant ainsi partiellement⁴² à la première critique formulée.

Rasoir d’Ockham

Quand on est confronté à plusieurs affirmations expliquant un même phénomène, le rasoir d’Ockham nous invite à privilégier l’affirmation la plus parcimonieuse. C’est à dire, l’affirmation qui requiert les hypothèses les moins coûteuses intellectuellement. Cependant, la signification de parcimonie ne va pas toujours de soi en l’absence de quantifications.
Voyons ce que l’approche bayésienne peut en dire. Admettons que l’on ait trois affirmations $A_1$ , $A_2$ et $A_3$ pour expliquer la même preuve P. les formules de Bayes s’écrivent alors :

$\begin{equation*} \begin{split} \Prob{A_1|P} & = \frac{\Prob{A_1}\Prob{P|A_1}}{\Prob{P}} \\ \Prob{A_2|P} & = \frac{\Prob{A_2}\Prob{P|A_2}}{\Prob{P}} \\ \Prob{A_3|P} & = \frac{\Prob{A_3}\Prob{P|A_3}}{\Prob{P}} \\ \end{split} \end{equation*}$

Chercher l’affirmation à privilégier revient à chercher l’affirmation la plus probable au vu de la preuve, donc la plus grande de ces trois probabilités. En multipliant toutes ces quantités par $\Prob{P}$ , on cherche donc l’affirmation maximisant $\Prob{A_i} \Prob{P|A_i}$ .
Ce qui peut se lire : Probabilité de l’affirmation $A_i$ multipliée par la probabilité d’observer la preuve $P$ sachant que l’affirmation $A_i$ est vraie. La formule de Bayes nous dit donc comment interpréter le terme « plus parcimonieux » du rasoir d’Ockham. Ce n’est donc pas simplement l’affirmation la plus probable qu’il faut privilégier, c’est à dire $\Prob{A_i}$ , mais bien le produit de cette probabilité avec la probabilité d’observer $P$ sachant que $A_i$ (l’exemple à venir rendra la nuance plus claire). On peut en déduire une nouvelle formulation pour le rasoir d’Ockham:

Rasoir d’Ockham bayésien :L’hypothèse maximisant $\Prob{A_i} \Prob{P|A_i}$ doit être privilégiée. C’est à dire l’hypothèse maximisant le produit de la probabilité de $A_i$ et de la probabilité d’observer la preuve $P$ sachant $A_i$ .

Cela peut sembler être une subtilité mais l’exemple suivant montre la différence induite par ce changement.

Exemple : Monsieur M. met dans une boite un chat et un souris. Dix secondes après il rouvre la boîte et la souris a totalement disparu. On peut émettre plusieurs affirmations :

$A_1$ = Le chat a mangé la souris
$A_2$ = La souris est passé dans une dimension différente pour échapper au chat
$A_3$ = Monsieur M. est magicien

Usons de notre rasoir d’Ockham bayésien pour voir quelle affirmation privilégier. On considère les probabilités a priori des affirmations suivantes : $\Prob{A_1} = 0.8$ : Les chats aiment manger des souris;
$\Prob{A_2} = 0.0000001$ : Je n’ai pas connaissance de souris ayant une telle capacité;
$\Prob{A_3} = 0.1$ : Je ne connais pas bien cette personne, mais il n’est pas impossible que ce soit un tour de magie.

Si on s’intéresse au curseur de vraisemblance utilisé classiquement en zététique, nous pourrions penser qu’il ne faut considérer que la probabilité a priori $\Prob{A_i}$ de ces affirmations. Ainsi il semblerait que l’affirmation $A_1$ soit à privilégier.
Considérons désormais la seconde partie du calcul uniquement (celle qui prend en compte la probabilité d’observer la donnée si l’affirmation est vraie), et que nous appelons la fonction de vraisemblance ou simplement vraisemblance. La donnée en l’occurrence est la révélation du contenu de la boite 10 secondes plus tard sans souris. On a alors par exemple : $\Prob{P | A_1} = 0.1$ : Seulement 10 secondes pour manger une souris et ne laisser aucune trace… ça me parait suspect; $\Prob{P | A_2} = 0.999$ : Si la souris avait un tel pouvoir elle aurait en effet sûrement disparu; $\Prob{P | A_3} = 0.95$ : Si Monsieur M. est magicien alors il est très probable que la disparition de la souris soit son tour de magie. En ne regardant que cette « vraisemblance », c’est alors le voyage inter-dimensionnel qui est à privilégier.

Dans un cadre bayésien, c’est la probabilité a posteriori que nous devrions regarder. C’est le produit des deux quantités précédentes⁴³. On trouve alors :

$\begin{equation*} \begin{split} \Prob{A_1}\Prob{P|A_1} &= 0.8 \times 0.1 = 0.08 \\ \Prob{A_2}\Prob{P|A_2} &= 0.0000001 \times 0.999 = 0.0000000999 \\ \Prob{A_3}\Prob{P|A_3} &= 0.1 \times 0.95 = 0.095 \end{split} \end{equation*}$

Au final, l’hypothèse à privilégier est que Monsieur M. est magicien…
Dans l’utilisation classique du rasoir d’Ockham cette précision n’est pas faite et le terme « affirmation la plus parcimonieuse » peut prêter à confusion.
On peut donc résumer le calcul ainsi :

$\begin{equation*} \begin{split} & \text{Probabilité a posteriori (ou \textit{posterior})} = \\ & \text{curseur de vraisemblance non bayésien (ou\textit{ prior})} \times \text{vraisemblance} \end{split} \end{equation*}$

Les termes posterior et prior sont communément utilisés dans le cadre bayésien comme indiqué dans la formule ci-dessus.

Maxime de Hume

Également appelée standard de Sagan, ou de Truzzi, ou de De Laplace⁴⁴, cette maxime postule que « Une affirmation extraordinaire requiert une preuve extraordinaire ».
Ici encore, nous allons voir que le cadre bayésien permet de retrouver et de préciser cette affirmation. Reprenons à nouveau la formule de Bayes :

(2) $\begin{equation*}\Prob{\text{Affirmation}|\text{Preuve}} = \frac{\Prob{\text{Affirmation}}\Prob{\text{Preuve}|\text{Affirmation}}}{\Prob{\text{Preuve}}}\end{equation*}$

Comme dit précédemment une affirmation est dite extraordinaire si elle est a priori très peu probable. Une telle affirmation vérifie donc $\Prob{\text{Affirmation}} = \epsilon$ , où $\epsilon$ est une quantité très petite. Pour que cette affirmation, une fois pris en compte le nouvel élément de preuve, soit vraisemblable, il faut donc une preuve qui mène à $\Prob{\text{Affirmation}|\text{Preuve}} \approx1$ . On peut montrer que cette condition⁴⁵ implique la relation suivante:

(3) $\begin{equation*}\Prob{\text{Preuve}} \ll \Prob{\text{Preuve}|\text{Affirmation}}\end{equation*}$

Ainsi pour qu’une affirmation a priori extraordinaire devienne vraisemblable il faut donc que la probabilité d’observer la preuve soit beaucoup plus petite que la probabilité d’observer la preuve sachant l’affirmation (nous verrons un exemple plus loin). La formule de Hume se déduit simplement en observant que comme toute probabilité est inférieur ou égale à $1$ on a $\Prob{\text{Preuve}|\text{Affirmation}} \leq 1$ et donc

(4) $\begin{equation*}\Prob{\text{Preuve}} \ll 1\end{equation*}$

Ainsi la probabilité d’observer la preuve doit être très petite. En d’autres terme, la preuve doit être extraordinaire⁴⁶ ! Ainsi, la formule de Bayes permet bien de démontrer la maxime de Hume.
Cependant la formule (3) en dit un petit peu plus :

la condition, $\Prob{\text{Preuve}} \ll 1$ n’est pas suffisante ! Il faut également que $\Prob{\text{Preuve}} \ll \Prob{\text{Preuve}|\text{Affirmation}}$ et donc que la probabilité d’observer la preuve sachant l’affirmation ne soit pas trop petite ! C’est à dire qu’il faut que la preuve soit ordinaire si l’affirmation est vraie : $\Prob{\text{Preuve}|\text{Affirmation}} \equiv 1$ .
On peut en déduire une nouvelle formulation pour la maxime de Hume.

Maxime de Hume bayésienne : Une affirmation extraordinaire requiert une preuve extraordinaire. Mais il faut aussi que la preuve soit ordinaire si l’affirmation est vraie.

Exemple :

Considérons l’affirmation $A =$ « les licornes existent » que l’on peut qualifier d’extraordinaire. J’y octroie a priori une probabilité de un sur un milliard : $\Prob{A} = 10^{-9}$ Pour que cette affirmation paraisse crédible, il faut donc observer une preuve $P$ vérifiant $\Prob{P} \ll \Prob{\text{P}|\text{A}}$ .
Considérons par exemple la preuve $P_1$ : « Quelqu’un a vu de loin une silhouette de cheval avec une corne sur le front ». Ce n’est pas une preuve si extraordinaire : il a pu se tromper, c’était peut-être une installation artistique, des petits malins ont pu attacher un postiche ou il a menti. J’estime la probabilité d’observer cela à un sur mille. On a donc $\Prob{P_1} = 0.001$ . En revanche, il est clair que la probabilité que quelqu’un ait vu de loin une silhouette de cheval avec une corne sur le front sachant que les licornes existent est très élevée : $P(P_1 | A) \approx 1$ .
On peut maintenant appliquer la formule de Bayes pour mettre à jour ma croyance en $A$ sachant $P_1$ :

$\begin{align*} \Prob{A|P_1} & = \frac{\Prob{A}\Prob{P_1|A}}{\Prob{P_1}} = \frac{10^{-9} \times 1}{0.001} = 10^{-6} \end{align*}$

Après cette preuve, j’octroie à l’existence des licornes une crédence de un sur un million. Cette preuve satisfaisait donc un seul des deux critères de la maxime de Hume bayésienne : elle est ordinaire si l’affirmation est vraie mais elle n’est pas extraordinaire en soi.
Au contraire prenons une autre preuve $P_2$ qui a une chance sur un milliard d’être observée : « J’ai fait 30 piles de suite ». La preuve est bien extraordinaire $\Prob{P_2} \approx 10^{-9}$ . Mais là encore la preuve ne satisfait qu’un seul des deux critères de la maxime de Hume baysésienne : elle est extraordinaire mais elle n’est pas ordinaire si l’affirmation est vraie. En effet, ici les deux évènements sont décorrélés : l’existence de licorne ne rend pas plus ordinaire une suite de 30 piles $P(P_2 | A) \approx 10^{-9}$ . Ça ne suffit donc pas à me convaincre. En l’occurrence la formule de Bayes donne:

$\begin{align*} \Prob{A|P_2} & = \frac{\Prob{A}\Prob{P_2|A}}{\Prob{P_2}} = \frac{10^{-9} \times 10^{-9}}{10^{-9}} = 10^{-9} \end{align*}$

Ce deuxième cas est caricatural mais il soulève une erreur de logique : se contenter d’une preuve extraordinaire sans vérifier que cette preuve est beaucoup plus probable dans l’affirmation qu’elle cherche à valider.
Enfin une preuve satisfaisante pourrait donc être $P_3$ un article scientifique corroboré par plusieurs chercheurs et fournissant suffisamment d’informations sur l’existence de licornes et étayé par des vidéos et des photos. Une telle preuve serait tout à fait extraordinaire en soi (estimée pour l’exemple à une chance sur 800 millions) et totalement ordinaire si l’affirmation est vraie (estimée ici à $0.99\%$ ). La formule de Bayes donne alors :

$\begin{align*} \Prob{A|P_3} & = \frac{\Prob{A}\Prob{P_3|A}}{\Prob{P_3}} = \frac{10^{-9} \times 0.99}{1.25*10^{-9}} = 0.792 \end{align*}$

Ma crédence en l’existence des licornes est donc passé à environ $80\%$ .

Conclusion

Voilà donc quelques idées sur la complémentarité entre bayésianisme et zététique. Nous avons montré d’abord quelques écueils possible de la démarche zététique et comment le cadre bayésien permets en partie d’y répondre. Dans une dernière partie nous avons montré comment la formule de Bayes permet de retrouver et préciser deux principes de la zététique : le rasoir d’Ockham et la maxime de Hume.
Bien d’autres pièces restent à ajouter au puzzle afin d’obtenir un paradigme plus solide. Quid des autres principes de la zététique ? Des biais cognitifs et des sophismes ? Quid de la charge de la preuve ? Est-ce que la perspective bayésienne permet d’en dire quelque chose, voire d’enrichir ces concepts ? Néanmoins, à l’avenir, si votre recette zététique semble mécontenter votre auditoire, essayer d’y rajouter une pincée de bayésianisme pour la rendre plus légère.

Conférence Esprit critique et sciences ( Lycée Fourcade – D.Caroti) : quelques extraits

3 septembre 20203 septembre 2020 Denis Caroti

Dans le cadre d’une conférence donnée en novembre 2019 au lycée Marie Madeleine Fourcade de Gardanne, notre collègue Denis Caroti avait été filmé… Mais l’enregistrement n’ayant pas les qualités attendues, nous lui avons demandé de publier certains extraits de celle-ci, en mode diaporama commenté, extraits que nous publions à présent. Cette conférence, organisée par Véronique Bianchi pour la « cafèt des sciences », était à destination des élèves et des enseignants et personnels présents. Merci à ces derniers pour leur accueil chaleureux en coulisse ainsi que pour toute l’attention des élèves pendant cette intervention.

Table of Contents

Esprit critique ?

Cette première « pastille » présente ce que l’on peut entendre par esprit critique en lien avec l’enquête et l’analyse de l’information : qu’est-ce que l’esprit critique et pourquoi s’en inquiéter ?

Quelques références pour aller plus loin :

Le rapport « Définir et éduquer l’esprit critique » produit dans le cadre des travaux de l’ANR « Éducation à l’esprit critique ».
Une interview donnée par Denis Caroti dans le cadre de cette ANR ainsi qu’un article en ligne sur ce site et un autre publié dans la revue de l’AFIS.
L’ouvrage « Esprit critique : outils et méthodes pour le second degré » publié par Canopé.
Un article de Serge Cospérec sur la pensée critique dans le milieu anglo-saxon.

Évaluer les preuves

Dans cette vidéo, après avoir défini la notion de preuve, on présente l’échelle des preuves ainsi que les différents sens du mot science, l’importance de préciser les types de registres qui s’entremêlent dans un débat ainsi que les limites et forces de la science en tant que démarche d’enquête et ensemble de connaissances.

Quelques références pour aller plus loin :

Sur l’échelle des preuves, une vidéo de notre collègue Christophe Michel (Hygiène Mentale), notamment à partir de 5’30.
Un article du Cortecs sur les différents sens du mot science.
L’excellent livre de notre collègue Guillaume Lecointre : Savoirs, opinions, croyances, chez Belin.

Prendre conscience de la limite de nos sens

Dans la vidéo suivante, on aborde la question de la faillibilité de nos sens à travers quelques exemples d’illusions d’optique classiques : l’objectif n’est pas de faire douter systématiquement de nos sens mais plutôt de faire comprendre qu’ils ne sont pas infaillibles : si l’on souhaite gagner en fiabilité, il sera alors utile (et rationnel) d’avoir recours à des preuves plus solides que notre seule expérience personnelle.

Pour aller plus loin :

Doit-on encore présenter le délectable cours en ligne de notre collègue et Cortexien de la première heure Richard Monvoisin qui aborde de nombreux exemples sur la limite de nos sens ?

Comment évaluer un témoignage ?

Dans cette partie, il est question d’apprendre à placer son curseur de vraisemblance en fonction du contenu du témoignage que l’on reçoit : toutes choses égales par ailleurs, plus une affirmation sort de l’ordinaire et des connaissances que l’on a, plus on doit exiger des preuves solides soutenant celle-ci. C’est, entre autre, ce que le philosophe David Hume relevait déjà il y a trois siècles dans son Enquête sur l’entendement humain mais aussi Laplace quelques années plus tard en écrivant : « De ce qui précède, nous devons généralement conclure que plus un fait est extraordinaire, plus il a besoin d’être appuyé de fortes preuves ; car, ceux qui l’attestent pouvant ou tromper ou avoir été trompés, ces deux causes sont d’autant plus probables que la réalité du fait l’est moins en elle-même. » (Théorie analytique des probabilités, 2e édition, 1812, p.17)

L’effet cigogne (ou comment ne pas confondre corrélation et causalité)

Dans cette vidéo, on aborde la fameuse confusion corrélation-causalité, que notre collègue Henri Broch a nommé « Effet cigogne » il y a déjà plusieurs années : un lien statistique entre deux variables (corrélation) n’implique pas forcément un lien de causalité entre celles-ci… Attention, la conclusion sur l’établissement du lien causal n’est pas l’objet de cette vidéo : pour en savoir davantage, voir les références ci-dessous.

Pour aller plus loin :

Un article sur la confusion corrélation-causalité
Une vidéo de la chaine Risque Alpha, qui aborde les critères de Bradford Hill permettant de conclure à une causalité.

Effet paillasson et impostures intellectuelles

Dans cette dernière vidéo, on présente ce qu’a nommé Henri Broch « l’effet paillasson » ainsi que les dérives qui y sont liées, notamment en termes d’impostures intellectuelles dans le champ du soin (avec le recours au verbiage pseudoscientifique).

Pour aller plus loin :

La vidéo d’Hygiène Mentale d’où est tiré l’extrait utilisé dans ce diaporama.
Le site du Gemppi qui a produit des vidéos pour expliquer en quoi ces dérives pouvaient être graves pour la santé des personnes
Sur l’effet paillasson et l’exemple du mot quantique : un article de Richard Monvoisin.

La COVID-19? Un bon prétexte pour causer démarche scientifique

10 juin 202011 juin 2020 Clara Egger

Les Presses Universitaires de Grenoble (PUG) ont profité de la crise du coronavirus pour proposer de la pensée critique au temps de cerveau disponible. Des membres et anciens membres du CORTECS ont ainsi pris la parole dans la série « Le virus de la recherche ». De belles pépites à lire et relire pour changer de Netflix.

« Non, non merci bien, moi vous savez le COVID ce n’est pas franchement ma tasse de thé… » On ne peut pas dire que Raul ait été d’emblée emballé par l’invitation des PUG. Il s’est finalement ravisé pour souligner que « contrairement aux activités de voyance, la science ne peut dire de l’avenir que ce que le passé nous permet d’inférer ». Une invitation à distinguer faits scientifiques et interprétation de ces faits, disponible en libre accès ici.

Nos deux amis, Nicolas et Richard, en routards de la pensée critique, invitent à la prudence quand il s’agit de se faire une opinion sur de telles questions de santé publique qui présentent un combo d’économie, d’infectiologie, de statistiques bayésiennes, de science politique et de philosophie morale. Grande est la tentation de donner son avis sur tout et n’importe quoi dans ce contexte.

Cours à l’ENSEEIHT

Etude de l’influence de la couleur d’éléments sur leur subitisation

La musicothérapie (et influence de la musique sur la pousse des plantes)

Influence de la construction d’un sondage sur les réponses des participants

La génération de l’aléatoire par le cerveau et les manières de l’influencer

Illusion sensorielle – Effet cutané du lapin (ECL)

Cours à l’IED 2 de Paris 8

Chemtrails, analyse d’une théorie complotiste

D’un point de vue narratif et esthétique

D’un point de vue éducatif et pédagogique

D’un point de vue humaniste

Pour conclure

Juger et choisir

Quand faut-il « dépendre » son jugement ?

Ce qui est et qui doit être

« Le sceptique, parce qu’il aime les hommes… »

Posture morale par défaut

Est-il possible d’échapper au choix ?

Quelles valeurs par défaut ?

Application : Zététique et psychophobie.

Présentation du projet

Description des ateliers

Jouer à débattre

Atelier philo

Fake news

Test de personnalité : l’effet Barnum

Principe de parcimonie et rasoir d’Occam

Échelle des preuves et curseur de confiance

Coïncidences…

Bilan

Les limites de l’approche zététique

Des principes dogmatiques

De bons outils dans des mains maladroites

Manque d’un formalisme mathématique

Manichéisme des arguments

Difficulté de conclure

Et donc ?

Les apports du bayésianisme

De la formule de Bayes

À la formule du savoir

Retour à la zététique

Les outils zététiques dans une main bayésienne

Rasoir d’Ockham

Maxime de Hume

Conclusion

Esprit critique ?

Évaluer les preuves

Prendre conscience de la limite de nos sens

Comment évaluer un témoignage ?

L’effet cigogne (ou comment ne pas confondre corrélation et causalité)

Effet paillasson et impostures intellectuelles

Cours à l’IED ² de Paris 8