Louis Paternault est enseignant de mathématiques au lycée Ella Fitzgerald de Saint Romain en Gal (69). Il nous présente ici une séquence effectuée avec ses élèves de seconde et première S concernant l’analyse des graphiques, en étudiant les différents biais qui peuvent se glisser dans leur réalisation et interprétation. Un travail précieux qui utilise des informations réelles, parues dans différents médias, renforçant l’idée que notre esprit critique gagne toujours à être en éveil face aux chiffres et autres présentations numériques dans la vie quotidienne. Merci et bravo à Louis !
L’article rédigé par Louis est déjà publié et mis en forme sur son blog, nous le reproduisons ici avec son autorisation.
[toc]
Objectif principal
Cette activité de lycée a pour but d’étudier différentes manières permettant de tromper (volontairement ou non) avec des graphiques. En d’autres termes, comment la représentation de vraies données statistiques permet de donner une impression erronée ?
Téléchargement
Pour les personnes pressées, commençons par les documents nécessaires pour réaliser cette séance en classes :
- le diaporama ;
- les polycopiés pour les deux groupes (groupe A et groupe B) ;
- l’énoncé de la séance sur tableur, ainsi que les données de travail ;
- l’ensemble des sources à compiler avec LuaLATEX
(fichiers LaTeX et images ; à décompresser avec le logiciel libre 7zip si votre système d’exploitation ne sait pas quoi faire de ce fichier).
Contexte
Cette séquence a été réalisée en accompagnement personnalisé, en seconde et en première S. Je pense qu’elle peut-être réalisée à n’importe quel niveau du lycée général.
Elle a été effectuée en demi-groupes (17 élèves environ).
Objectifs de la séquence
En ce qui concerne le programme de mathématique, cette séquence permet de :
- lire, analyser, créer différentes représentations de séries statistiques ;
- « faire réfléchir les élèves sur des données réelles et variées » (programme de seconde) ;
- manipuler le tableur (principalement pour représenter une série statistique).
Pour l’esprit critique, cette séquence permet :
- de voir comment les mêmes données peuvent donner une impression différente selon la manière dont elles sont représentée ;
- d’apprendre à ne pas se laisser tromper par de telles erreurs (volontaires ou non).
Déroulement
Cette séquence se déroule en deux parties (d’environ une séance chacune) : dans un premier temps, les élèves étudient des graphiques « réels » (publiés dans des journaux, à la télé, par des partis politiques, etc.) pour établir une liste d’erreurs fréquentes ; dans un second temps, ils sont amenés à créer eux-même un graphique trompeur (qui, à partir de vraies données, donne une impression fausse ou fantaisiste).
Première séance : Analyse de graphiques
Note : J’ai réalisé d’abord cette séance ; ma collègue Céline l’a utilisée et améliorée. C’est sa version que je décris ici.
La professeure commence par présenter oralement l’objectif de la séance :
À partir de données réelles : répertorier différentes manières de tromper les autres en construisant des graphiques (et donc, répertorier aussi des pièges à éviter pour ne pas se tromper en observant des graphiques).
Travail en groupe
Les élèves sont séparés en deux groupes, et doivent prendre un stylo chacun. Chaque groupe se voit distribuer :
- les polycopiés groupeA.pdf pour le premier groupe, groupeB.pdf pour le second groupe (dans chacun des deux polycopiés, les mêmes données sont représentées de deux manières différentes, menant à des conclusions différentes) ;
- des post-it.
Les élèves ont eu quelques minutes pour analyser chaque graphique et prendre des notes de leurs idées (une par post-it).
Mise en commun
La professeure leur présente la première partie du diaporama (qui reprend les graphiques qu’ils ont eus entre les mains), en leur disant qu’il s’agit des graphiques qu’ils ont analysés sur polycopié, et qu’ils vont répertorier aux tableaux chacune des « manipulations » possibles.
Leurs idées (d’erreurs ou manipulation) sont relevées au cours du diaporama, à partir de leurs post-it, et des nouvelles idées qui peuvent alors venir.
À la fin de cette partie, une liste des erreurs possibles est disponible au tableau (voir ci-dessous).
Nouveaux graphiques
La seconde partie du diaporama est alors projetée, et les élèvent doivent identifier pourquoi les graphiques proposés sont trompeurs, en se référant à la liste construite précédemment.
Seconde séance : Création d’un graphique trompeur
Note : Cette séance n’a pas été réalisée entièrement ; je pense qu’elle prend une ou deux séances d’une heure.
Cette séance se déroule sur tableur, par binôme. Le but de la séance est de créer un graphique trompeur (réalisé à partir de vraies données, mais qui donne une impression fausse ou fantaisiste).
Première partie
Les élèves ont à disposition l’énoncé, et des séries de données statistiques (réelles, mais a priori sans lien entre elles).
Ils doivent tracer différents graphiques (le détail est dans l’énoncé) ; le but est de leur faire manipuler le tableur (différents types de graphiques, plusieurs axes pour un même graphique, axes ne commençant pas à zéro, etc.).
Seconde partie
Après avoir vu comment manipuler des graphiques, c’est au tour des élèves de produire un graphique trompeur : ils doivent produire un graphique qui montre une corrélation entre deux des séries données pourtant sans lien entre elles.
Les données (population, nombre de mariages, dépenses en fruit et légume, entrées au cinéma en France depuis 1960) sont dans un fichier donnees.ods (sur lequel ils ont travaillé dans la partie précédente). Les élèves peuvent sélectionner les données représentées, supprimer celles qui ne servent pas leurs objectifs, mais ils n’ont pas le droit d’inventer ou modifier des données.
Troisième partie
Enfin, il est possible de terminer (je ne l’ai pas fait ; voir la partie Bilan) en faisant présenter aux élèves leurs corrélations bidon de manière aussi convaincante que possible : en les faisant trouver des fausses explications (« la consommation de légumes favorise les mariages car… ») ou des conséquences (« il faut encourager les français à aller au cinéma pour que la consommation de fruits et légumes augmente »).
Bilan
Analyse de graphiques
Les élèves ont semblé apprécier cette séance : ils ont été très dynamiques. Ils ont bien détecté les problèmes et ont fait des commentaires intéressants sur les différents thèmes. L’objectif de la séance (remarquer des erreurs dans les graphiques) semble donc atteint.
Création d’un graphique trompeur
Je n’ai réalisé que partiellement cette séance (j’ai commencé, mais les vacances sont arrivées, et des séances ont été annulées, et finalement, la suite se serait déroulée plus de six semaines après la première partie ; j’ai préféré abandonner) ; ma collègue ne l’a pas réalisée (à cause de la fin de l’année), donc le bilan est très partiel.
La création de graphiques (pas encore trompeurs) a plutôt fonctionné, en demandant leur attention régulièrement pour expliquer comment faire certains gestes techniques (calcul en base 100, deux axes différents, etc.). Comme alternative, je vois :
- faire un sujet très dirigé (mais je voulais les laisser tâtonner, pour qu’ils apprennent à chercher) ;
- distribuer un mémo sur l’utilisation des graphiques avec LibreOffice.
Seuls quelques binômes se sont essayés à la création de graphiques trompeurs, et seul l’un d’entre eux a été jusqu’au bout, et a réussi à montrer une relation entre deux séries a priori indépendantes. Les autres n’ont pas terminé par manque de temps.
Je pense qu’une séance d’une heure ne suffit pas à faire cette partie : deux séances devraient convenir. La dernière partie (présenter à la classe son graphique) peut servir de variable d’ajustement si les élèves ont terminé trop tôt.
Liste des erreurs
Les erreurs analysées dans cette séquence sont les suivantes :
- Utiliser une échelle logarithmique au lieu d’une échelle linéaire (cela peut être parfois très utile, mais c’est trompeur si on ne fait pas bien attention).
- Ne pas faire commencer l’axe des ordonnées à 0 (très courant).
- Utiliser la 2D ou la 3D pour donner de fausses impressions (doubler l’échelle multiplie les aires par quatre, et les volumes par huit).
- Trier les données : effacer celles qui ne nous plaisent pas (particulièrement efficace en sélectionnant la période de temps qui sert notre propos).
- Choisir la bonne année de référence pour des indices en base 100 (ce qui est la raison d’être des indices, mais qui peut créer un effet exagéré par rapport à la réalité des données).
Exemples traités
Je donne pour chacun des exemples la question posée aux élèves, sur laquelle porte la manipulation ou l’erreur du graphique.
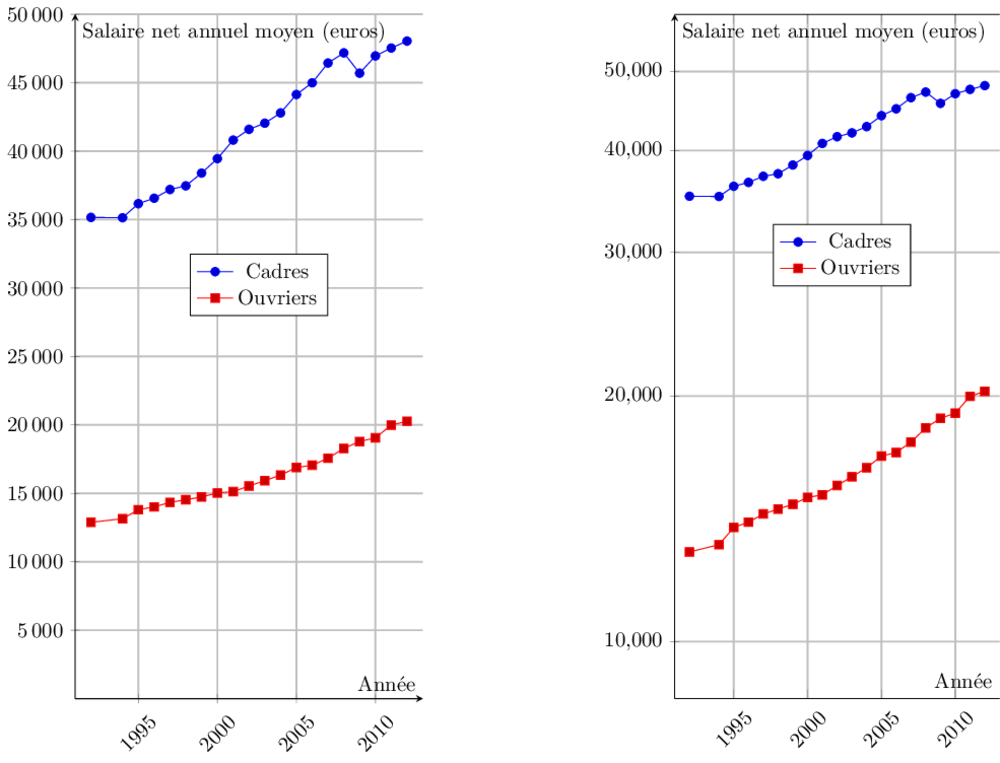
Évolution des salaires
Qui, des cadres ou des ouvriers, a vu son salaire annuel net moyen augmenter le plus entre 1992 et 2012 ?
Le graphique de droite utilise une échelle logarithmique, alors que celui de gauche utilise une échelle linéaire (à laquelle nous sommes le plus habitués). Ce que montrent ces graphiques, c’est que le salaire des cadres augmente le plus en valeur absolue (graphique de gauche), alors que c’est le salaire des ouvriers qui augmente le plus en taux d’évolution (graphique de droite).
Laquelle des deux réponses est la bonne ? C’est une question politique, pas mathématique.
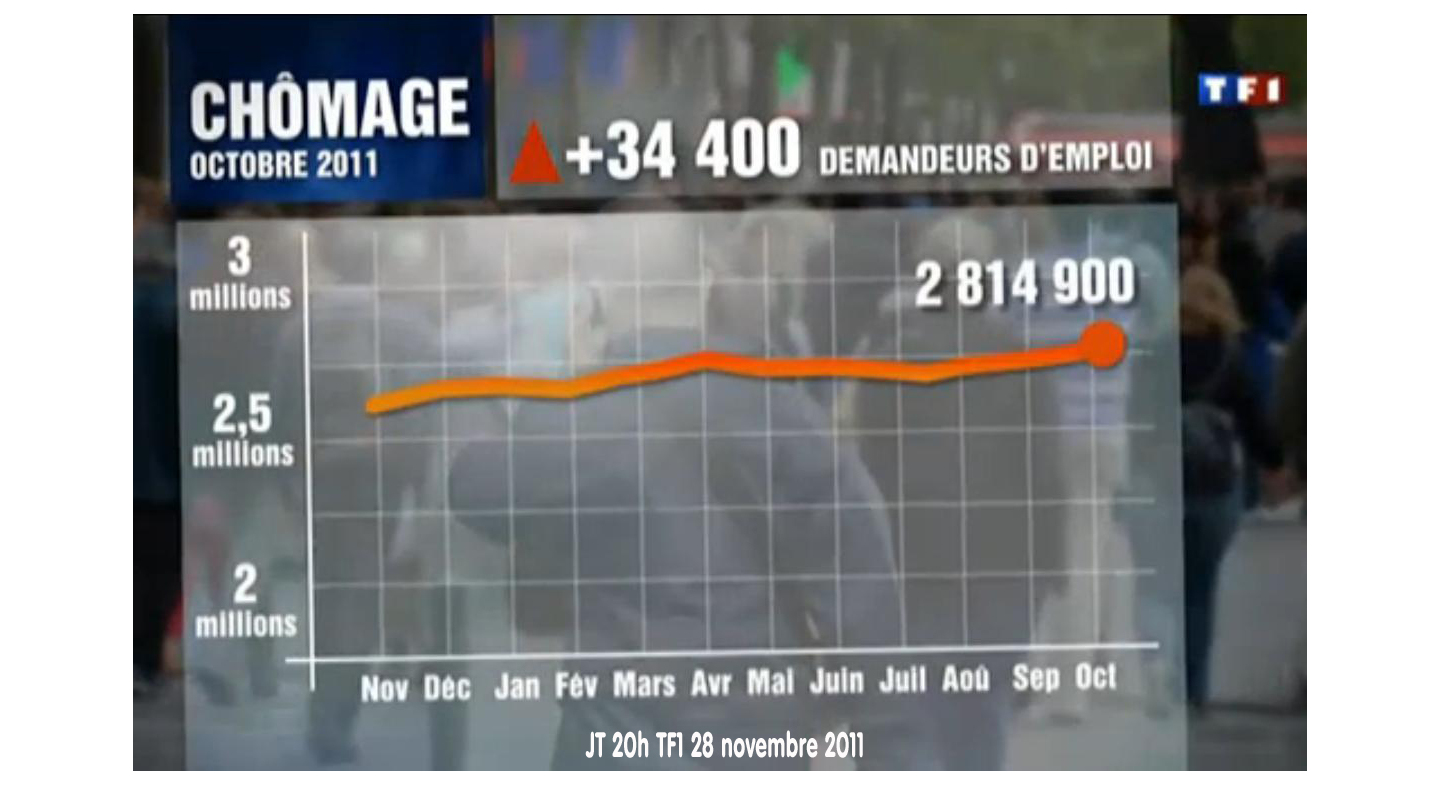
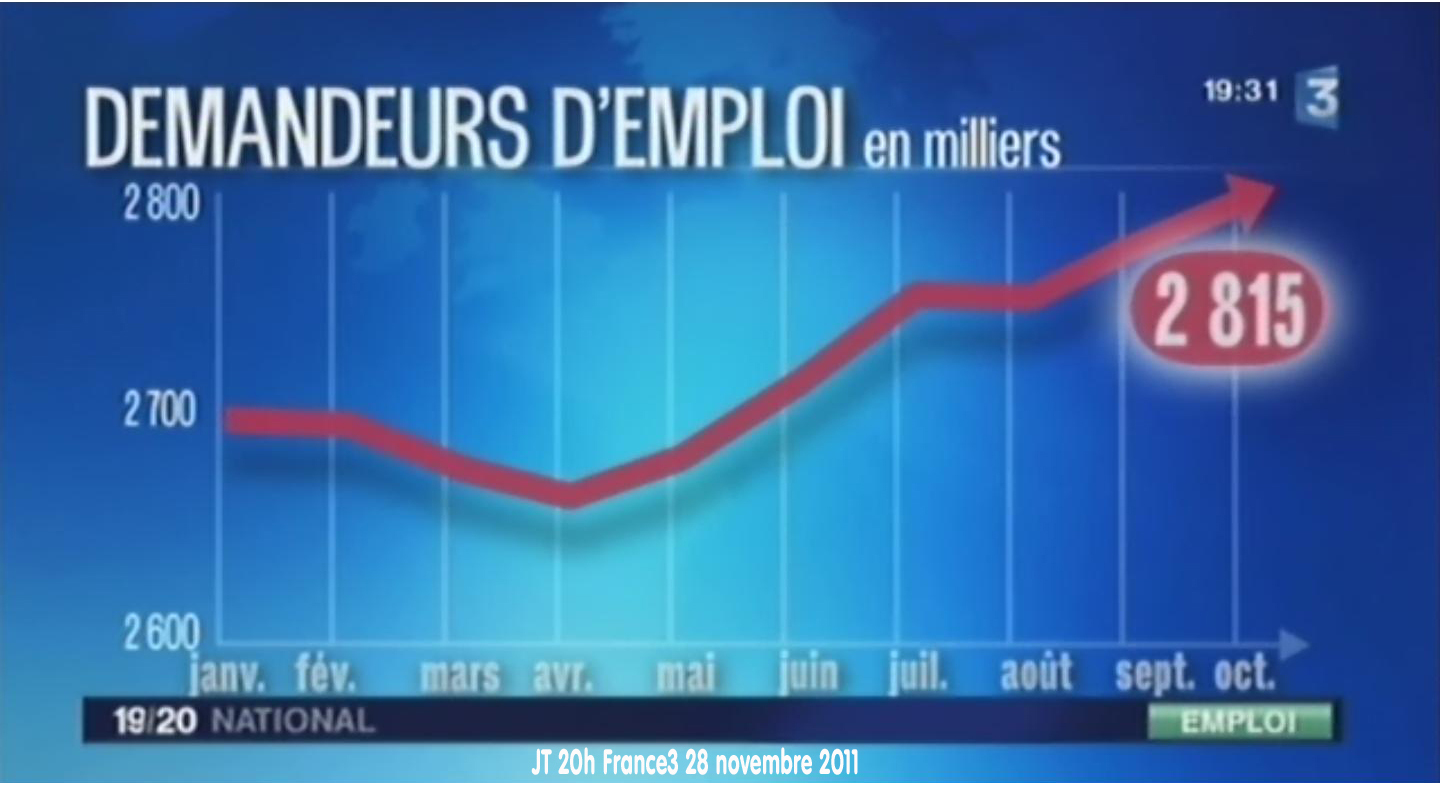
Évolution du chômage
Le chômage a-t-il :
- un peu, ou pas augmenté ?
- moyennement augmenté ?
- beaucoup augmenté ?
Ces trois graphiques présentent la même information (les mêmes données) de trois manières différentes.
- Sur aucun des trois graphiques, l’échelle verticale ne commence à zéro (et sur celui de France 2, elle n’est même pas présente) : cela augmente artificiellement les évolutions.
- La légende de l’axe horizontal est difficilement lisible.
Évolution du taux de grévistes
Le nombre de grévistes a-t-il :
- peu diminué ?
- beaucoup diminué ?
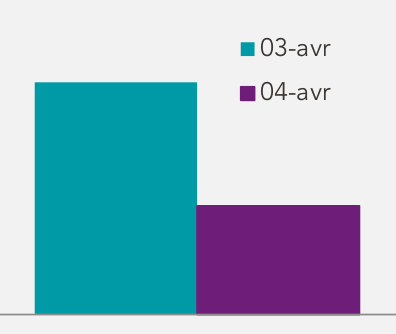
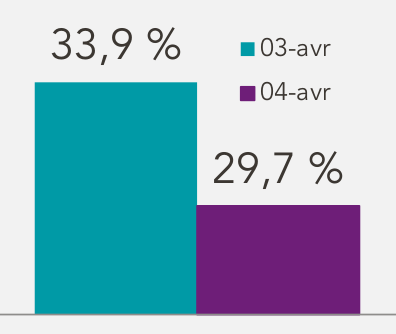
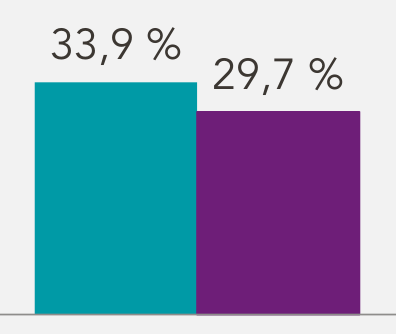
D’après le communiqué de presse de la SNCF du 4 avril 2018 ; relevé par l’émission C’est à vous du 6 avril 2018 (France 5).
L’erreur ici est que l’échelle verticale ne commence pas à 0.
Il est intéressant de rappeler le contexte : ce communiqué a été publié durant une grève des cheminots contre la direction de la SNCF (et plus largement contre une mesure du gouvernement) ; la direction de la SNCF a tout intérêt à minimiser le succès de la grève, pour décourager les cheminots et rassurer les usagers.
Part de marché
Quelles sont (dans l’ordre) les trois premières marques de smartphones en fonction de leur part de marché ?
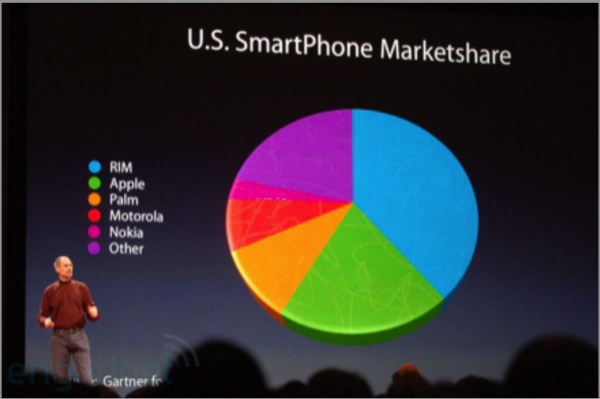
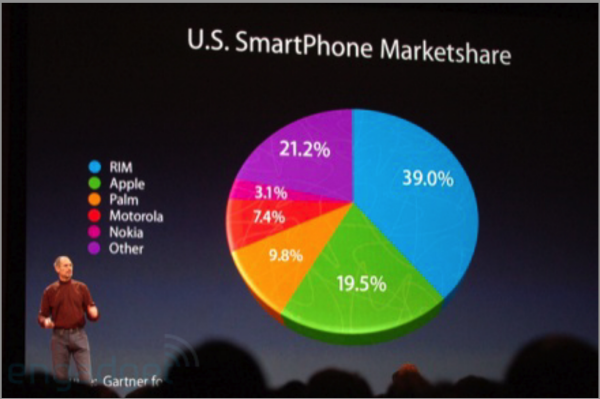
D’après une conférence de presse d’Apple (laquelle ?), repéré par Vandy Berten.
La 3D donne l’impression que la section verte est plus grosse que la violette, mais c’est l’inverse qui est vrai.
D’une manière générale : ne jamais utiliser de 3D dans les graphiques : c’est joli, mais ça fausse très souvent les résultats.
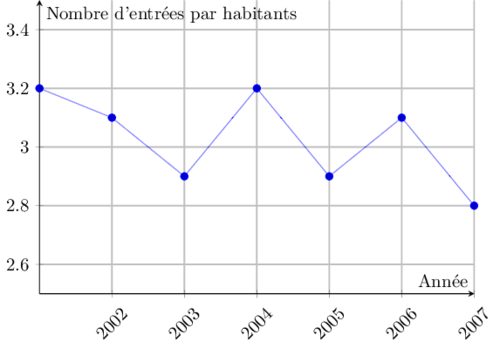
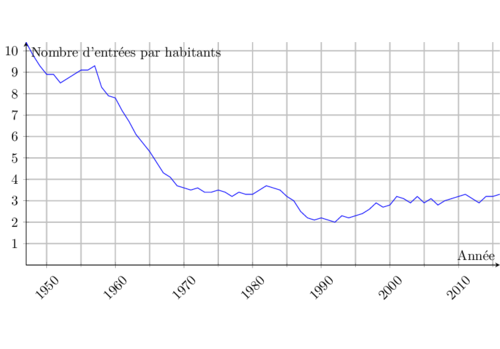
Évolution de la fréquentation des cinémas
La démocratisation d’internet en France (à partir des années 2000) a-t-elle eu un effet négatif/neutre/positif sur la fréquentation des français au cinéma ?
Les personnes luttant contre le téléchargement illégal affirment souvent que le « piratage » tue le cinéma. Ces données le prouvent-elles ?
Si l’on regarde le premier graphique, qui ne présente que les données sur la période 2001—2007, on a l’impression que la fréquentation stagne, voire décroît. En revanche, en regardant les données depuis les années 50 (second graphique), on voit que la fréquentation a plutôt tendance à augmenter ces dernières années.
Ici, selon la période de temps présentée, on montre un effet ou son contraire.
Aires de disques
En regardant le premier graphique :
- Le disque rose est « combien de fois » plus grand que le disque vert ?
- Quel pourcentage représente-t-il ?
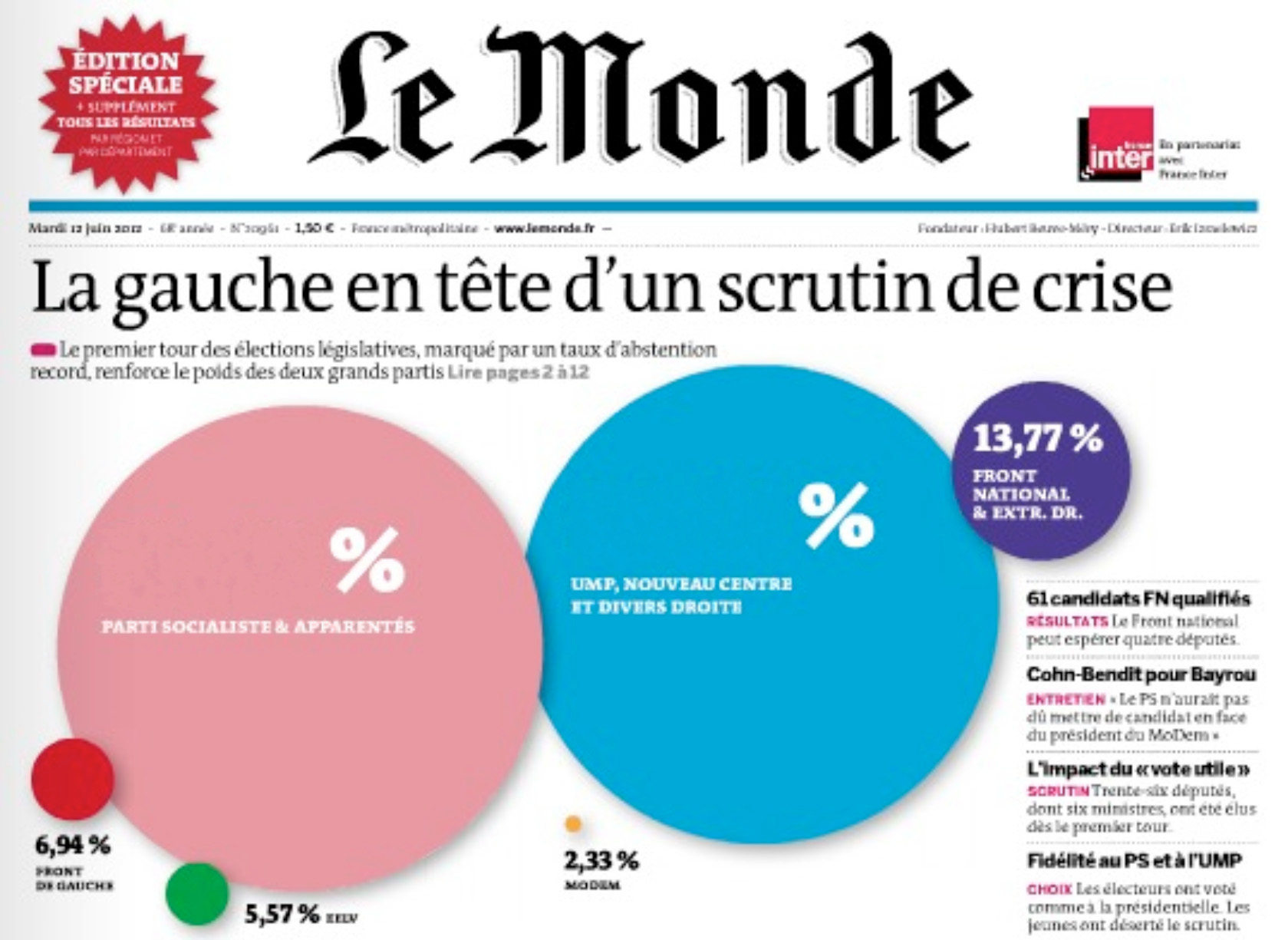
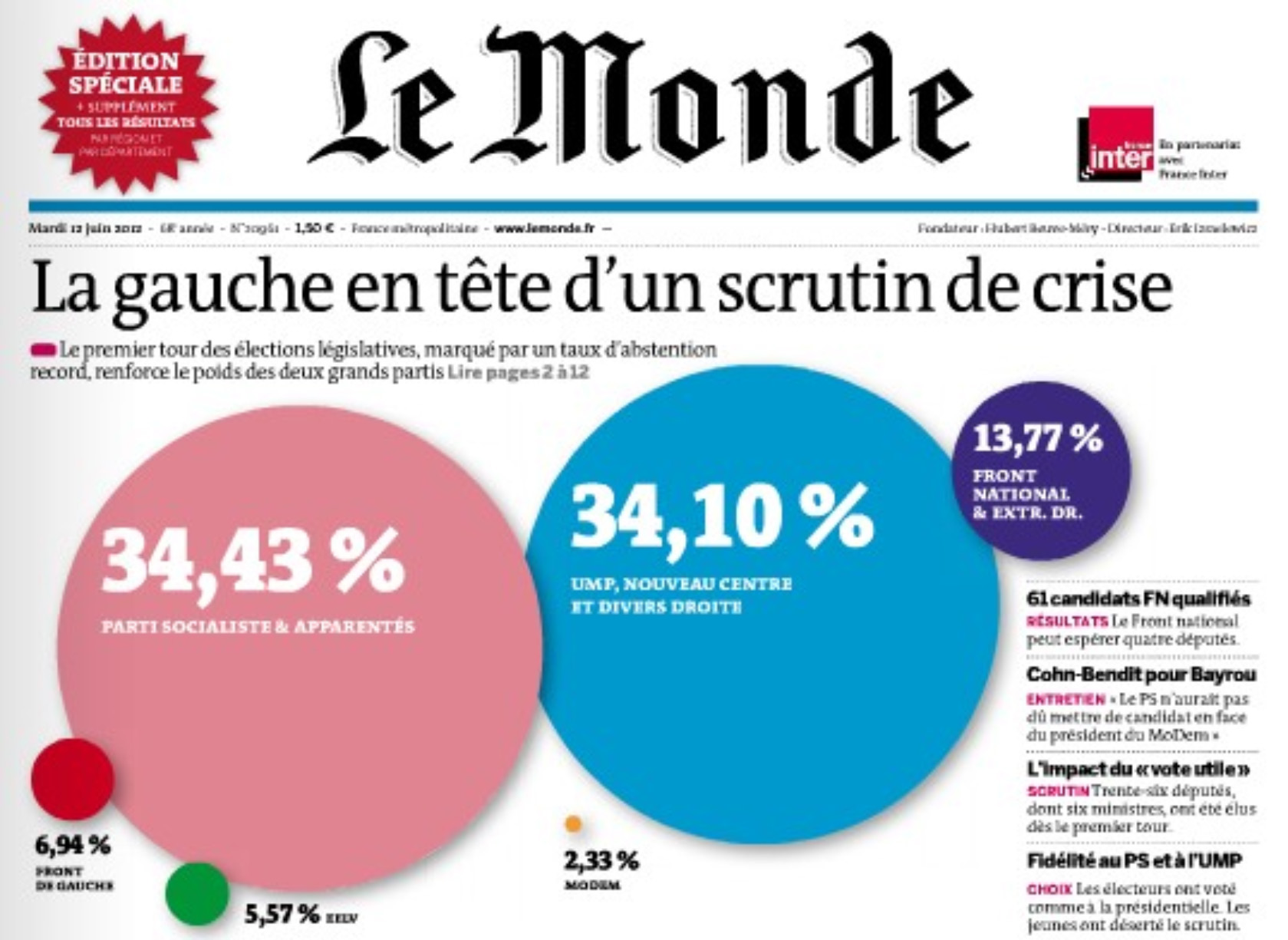
Source : Le Monde, édition du 12 juin 2012.
Les rayons des cercles sont proportionnels aux pourcentages, mais les aires donnent du coup une impression faussée. Si les rayons des cercles rose et vert sont proportionnels aux pourcentage (environ six fois plus grand), les aires ne le sont pas : l’aire du disque rose est 36 fois celle du disque vert.
Il y a deux problèmes ici.
- D’une part, sur un graphique en deux dimensions (comme ici) ou en trois dimensions, une multiplication de l’échelle par deux produit une multiplication de l’aire par 4, et du volume par 8, ce qui est trompeur (attention donc aux graphiques qui, par exemple, pour représenter l’évolution des dépenses de santé, représentent un hôpital plus ou moins gros : est-ce que l’échelle est proportionnelle aux données, ou le volume ?).
- D’autre part, l’œil et le cerveau humains savent bien comparer des distances (hauteur ou longueur), mais ne sont pas bons pour comparer des aires (cité par Vandy Berten dans la partie Confondre surface et taille de son article Comment mentir avec un graphique).
Conclusion : Ne pas utiliser de 2D ou 3D (ou alors faire très attention).
Radicalisation en France
Voir la version sans légende sur laquelle travailler en classe.
- Classer les couleurs par nombre de cas signalés.
- Quelle est la particularité des départements noirs ?

Deux erreurs faussent cette cartographie :
- Le choix des couleurs n’est pas usuel. Le plus souvent, pour montrer une gradation de données, les couleurs utilisées vont du plus clair au plus foncé (exemple), ou suivent plus ou moins le spectre lumineux (exemple). Sur cette carte, comparer deux départements sans se référer à la légende n’est pas évident.
- Les données représentées sont des données brutes, et non pas relatives. Ce graphique montre que dans les départements les plus peuplés sont relevés le plus grand nombre de cas de radicalisation, ce qui est tout à fait normal si le taux de radicalisation est indépendant de la géographie (voir une présentation humoristique de ce problème).
Tract électoral
Quel procédé a été utilisé pour renforcer l’argument de ce tract électoral ?
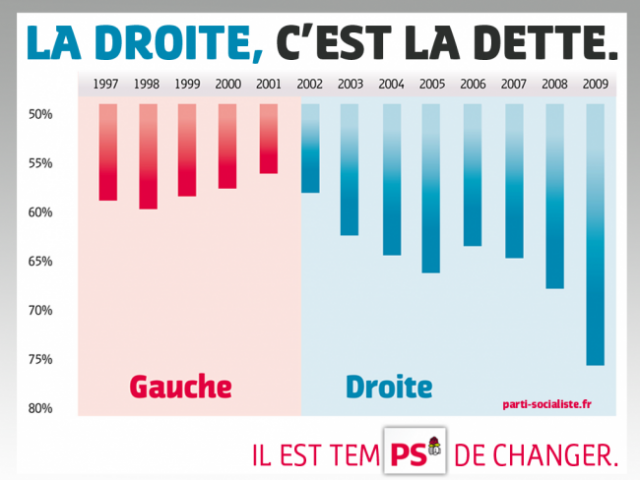
L’échelle verticale ne commence pas à 0.
Chiffres de la délinquance
En quoi l’utilisation du graphique par Brice Hortefeux (alors ministre de l’intérieur, donc en charge de la délinquance) est-elle fallacieuse ?
Source : Journal télévisé du 20 janvier 2011, TF1 (repéré par le Cortecs).
- Un premier problème classique est que l’échelle verticale est absente. Il est assez facile d’observer qu’elle ne commence pas à zéro.
- Le titre est particulièrement vague : Qu’est-ce qui est mesuré ici ? La délinquance réelle ? Le nombre de plaintes ? On a vu des policiers jouer avec les chiffres (faire déposer une plainte par personne à un groupe de personnes pour augmenter ces chiffres ; requalifier une tentative de cambriolage en destruction de biens pour transformer un crime en délit). Les violences interpersonnelles (violences conjugales par exemple) semblent augmenter, mais c’est plutôt dû au fait que les victimes portent maintenant plus souvent plainte (pour une analyse plus approfondie, voir cet article écrit en réaction à ces annonces de Brice Hortefeux). Le nombre de plaintes n’est donc pas un bon indicateur de la délinquance.Est-ce la délinquance ressentie qui est mesurée ? Celle-ci augmente plutôt, alors que le monde n’a jamais été aussi peu violent.Bref, avec assez peu de rigeur (ou beaucoup de mauvaise foi), il est possible de faire dire à peu près n’importe quoi aux chiffres de la délinquance.
Production industrielle
Pouvez-vous classer les quatre pays représentés en fonction de leur production industrielle en 2015 ?
Source : Débat télévisé du 20 mars 2017 (durant la campagne pour l’élection présidentielle). Marine Le Pen a publié ce graphique sur son compte Twitter.
Ce classement n’est pas celui représenté sur le graphique qui représente des indices, base 100 en 2001 (année d’introduction de l’euro). En choisissant une autre année de référence, on obtient des graphiques dans lesquels l’effet annoncé par Marine Le Pen, s’il est toujours présent, est beaucoup moins impressionnant.
Les « décodeurs » du Monde font une analyse détaillée de ce graphique.
Corrélation n’est pas causalité 1
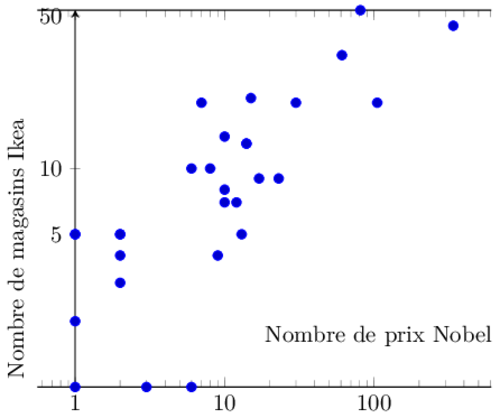
Quel est le lien entre le nombre de magasin Ikéa dans chaque pays, et son nombre de prix Nobel ?
Commençons par remarquer que j’ai supprimé de ce graphique les données qui ne servaient pas mon propos (comme la Chine, qui a beaucoup de prix Nobel, mais peu de magasin Ikéa).
Une règle bien connue des zététiciens est « Corrélation n’est pas causalité ». Il est probable que le nombre de magasins Ikéa dans un pays soit corrélé au nombre de prix Nobel, mais ce n’est pas pour autant que l’un est la cause de l’autre. Dans ce cas, il y a sans doute un troisième facteur qui est la cause de cette corrélation : le niveau de vie. Plus le niveau de vie d’un pays est élevé, plus il y aura de magasin Ikéa et de prix Nobel.
Un autre exemple célèbre est que dans les écoles, la taille des pieds (la pointure) est corrélée au niveau de lecture : en général, les élèves qui ont les plus grands pieds savent mieux lire que les autres. Bien qu’étrange à première vue, ce lien est parfaitement normal : les élèves plus agés ont des pieds plus grands, et savent mieux lire.
Conclusion : Ce n’est pas parce que deux mesures sont liées que l’une est la cause de l’autre.
Corrélation n’est pas causalité 2
Quel est le lien entre le nombre de divorces dans le Maine (un état américain) et la consommation de margarine (aux États-Unis ?) ?
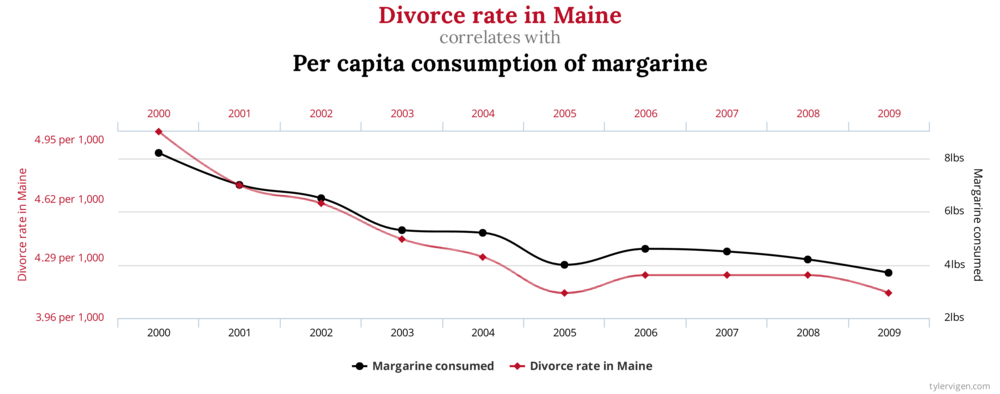
Encore une fois, corrélation n’est pas causalité. Mais cette fois-ci, contrairement à l’exemple précédent, il n’y a sans doute pas de liens entre les deux séries de données : ce n’est probablement qu’un hasard.
Les zététiciens disent également que « L’improbable est probable ». S’il est quasiment impossible que deux séries statistiques prises au hasard soient corrélées, il est tout à fait normal que, parmi les milliards de séries statistiques qui existent dans le monde, plusieurs séries sans lien entre elles varient de la même manière. C’est ce qui se passe ici.
Variations et Valeurs cumulatives
Je n’ai pas utilisé cet exemple avec mes élèves, mais en utilisant les valeurs cumulatives plutôt que les valeurs absolues, il est possible de donner une impression fausse. Vandy Berten donne un exemple dans Comment mentir avec un graphique.
Bibliographie
J’ai puisé mes exemples de graphiques trompeurs dans les articles suivants (mais pas uniquement).
- Nicolas Gauvrit : Graphiques, attention aux axes !
- Denis Caroti, Alain Le Métayer, Guillemette Reviron : Mathématiques – Comment tromper avec des graphiques.
- Vandy Berten : Comment mentir avec un graphique.
- Mathilde Damgé : Sept conseils pour ne pas se faire avoir par les représentations graphiques.
- Étienne Ghys : Graphiques frelatés.