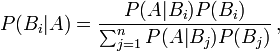Voici la solution au jeu des trois boîtes, ou problème de Monty Hall, donnée par Louis Dubé, et complétée par le CorteX.
Pour revenir à l’énoncé, voir ici.
Voici différentes approches de la version initiale
Table des matières
Explication de Louis Dubé
La bonne réponse est la 2 : je change mon premier choix
La meilleure stratégie est de TOUJOURS changer son premier choix. En conservant votre premier choix, vous
ne changez pas de probabilité de succès, qui demeure un tiers. En changeant toujours de choix, vos chances de succès sont deux fois plus grandes. Car, en dévoilant l’une des boîtes qui n’a pas d’argent sous elle, le maître de cérémonie vous offre effectivement l’ensemble des deux choix qui restent, dont la probabilité égale deux tiers. La figure ci-contre illustre ce concept.
L’illusion est de penser que s’il reste deux choix et qu’on ignore lequel, notre premier choix est aussi bon que le deuxième offert (soit 50 %).
Tentez vous-mêmes l’expérience : un joueur cache l’argent sous l’une des trois boîtes à l’insu d’un deuxième joueur; le deuxième joueur tente de deviner où le premier joueur a caché l’argent en utilisant systématiquement – pendant disons 30 coups – l’une ou l’autre des stratégies proposées. Vous obtiendrez environ 20 succès sur 30, en suivant la stratégie de toujours changer de choix ; deux fois mieux que si vous gardiez toujours votre premier choix.
Une autre façon de saisir l’importance de changer son premier choix est de considérer un problème similaire : au lieu de trois boîtes, supposons que le choix original vous propose un millier de boîtes, dont une seule contient l’argent convoité. Vous choisissez au hasard la boîte N°527. Pour vous aider, le maître de cérémonie dévoile 998 boîtes qui ne contiennent pas d’argent, seule la boîte N°721 demeure, ainsi que votre choix original : la boîte N°527. Garderiez-vous votre choix original qui n’avait qu’une chance sur mille de contenir l’argent ? Croyez-vous vraiment que votre premier choix aurait maintenant une probabilité de 50 % ? Il apparaît évident que vous changeriez de choix en croyant (justement) qu’il y a beaucoup plus de chances (999 chances sur 1000) que l’argent se trouve sous la seule boîte (autre que votre choix original) qui n’a pas été dévoilée.
Louis Dubé
Approche expérimentale
Louis Dubé suggère à tout élève de collège de rendre fous ses professeurs en leur faisant une simple démonstration sur 30 essais. Personnellement, je vais essayer de le faire aux étudiants de zététique avec des gobelets, un euro et deux chewing gum mâchés (je viendrai raconter l’expérience).
Explication de Guillemette Reviron
À l’issue du premier tirage, la probabilité que je sois tombée sur la bonne boîte est de 1/3 et la probabilité que je me sois trompée, c’est-à-dire que la bonne boîte soit une des deux autres, est de 2/3. L’animateur ouvre ensuite une boîte vide. Cette petite manipulation ne change pas ces probabilités puisque le choix de la boîte a été fait avant :
– la probabilité d’être tombée sur la bonne boîte vaut toujours 1/3
– la probabilité que ce ne soit pas la bonne vaut toujours 2/3.
Ce qui a changé, c’est qu’à la première étape, si je me suis trompée, l’argent est sous l’une des deux autres boîtes alors qu’à présent, si je me suis trompée, l’argent est sous la seule autre boîte. J’avais 2 chances sur 3 qu’elle soit sous une des autres boîte, j’ai deux chances sur trois qu’elle soit sous l’autre boite.
Le tour est joué !
Regardez, j’ai parié, et j’ai gagné deux bouteilles de vin.
Explication grâce à l’arbre des possibles
Voici les versions (en anglais) de la version des tasses et (en français) de celle voiture/chèvres.
Démonstration à l’aide du théorème de Bayes
Pour des étudiants d’un certain niveau en mathématiques, on pourra résoudre le « paradoxe » avec le théorème du révérend Bayes, qui nous dit :
Soit un événement quelconque, et soit (Bi)i=1..n un ensemble d’événements à la fois exhaustifs et mutuellement exclusifs. Alors pour tout 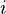 , on a :
, on a :
Supposons que je choisisse la boite n°3 – le raisonnement serait identique dans les deux autres cas – et notons :
– F1 (respectivement F2 et F3) : la voiture se trouve dans la boite n°1 (resp. 2 et 3)
– O1 (respectivement O2 et O3): l’animateur ouvre la boite vide n°1 (resp. 2 et 3)
Supposons alors que l’animateur ouvre la boite 1 – le raisonnement est le même s’il ouvre la boite 2.
La probabilité de gagner en changeant mon choix est alors la probabilité que la voiture soit dans la boite 2 sachant que l’animateur a ouvert la boite n°1, c’est-à-dire P(F2/01). Or, d’après la formule de Bayes.
En effet, si la voiture est dans la boite 2 et que j’ai choisi la boite 3 au premier tirage, la seule boite que peut ouvrir l’animateur est la boite n°1 donc P(01/F2) = 1.
De la même manière, si la voiture est dans la boite 1, l’animateur ne peut pas l’ouvrir donc P(O1/F1)=0 et si la voiture est dans la boite 3, l’animateur a deux choix équiprobables (la boite 1 ou la boite 2) donc P(O1/F3) = 1/2.
Pour aller plus loin
- On retrouvera également une simulation avec chèvres et voiture sur le site du Laboratoire de Mathématiques Raphaël Salem de l’Université de Rouen (ici).
- Pour les fans de l’utilisation des sciences dans les fictions, voici un extrait de Las Vegas 21, de Robert Luketic (2008) lors duquel l’enseignant (Kevin Spacey) pose la question à ses étudiants – dont le jeune héros (Jim Sturgess) qui répond bien (extrait en anglais – je cherche une version originale sous-titrée, en attendant contentons-nous du doublage français)
[youtube=http://www.youtube.com/watch?v=huLoJcTppXk]
- Pour l’histoire, il semble que la paternité de ce dilemme revienne à Joseph Bertrand (ci-contre) en 1889, sous le nom de « Paradoxe de la boîte de Bertrand ».
 Puis c’est le regretté Martin Gardner, incontournable pionnier de la pensée critique décédé en 2010, qui l’exhuma en 1959 dans sa rubrique Mathematical Games du Scientific American sous le nom de « problème des trois prisonniers » (« Mathematical Games » column, Scientific American, October 1959, pp. 180–182). Enfin, c’est Steve Selvin qui rouvrit la question dans « A problem in probability (letter to the editor)« , American Statistician 29 (1): 67 (February 1975) et « On the Monty Hall problem (letter to the editor) », American Statistician 29 (3): 134 (August 1975).
Puis c’est le regretté Martin Gardner, incontournable pionnier de la pensée critique décédé en 2010, qui l’exhuma en 1959 dans sa rubrique Mathematical Games du Scientific American sous le nom de « problème des trois prisonniers » (« Mathematical Games » column, Scientific American, October 1959, pp. 180–182). Enfin, c’est Steve Selvin qui rouvrit la question dans « A problem in probability (letter to the editor)« , American Statistician 29 (1): 67 (February 1975) et « On the Monty Hall problem (letter to the editor) », American Statistician 29 (3): 134 (August 1975).
-
Un site est entièrement consacré au problème, ainsi qu’un livre : Jason Rosenhouse, The Monty Hall problem – The Remarkable Story of Math’s Most Contentious Brain Teaser (Oxford University Press 2009).
 Louis Dubé nous offre en prime un court programme commenté en langage Basic qui simule ce problème avec « N » boîtes (donc aussi avec 3 boîtes).
Louis Dubé nous offre en prime un court programme commenté en langage Basic qui simule ce problème avec « N » boîtes (donc aussi avec 3 boîtes).
Voici :
- le code du programme avec commentaires.
- Le code source en fichier texte (qui peut facilement être copié)
- Les résultats pour 9 essais (chaque étape en détail pour bien saisir le processus) et les résultats cumulatifs pour 9 essais et pour 1000 essais.