Mensonges, sacrés mensonges et modèles de régression

20 février 20224 mars 2022 Nicolas Martin et Alexandre Changenet

Quel sera le record du 100m en 2100 ? C’est une question que se sont posée des chercheurs anglais dans un article de 2004 et qui, pour y répondre, ont déployé leurs outils statistiques de manière assez maladroite. Une erreur qui n’est qu’une perche tendue pour faire une lecture critique d’un article scientifique et montrer comment on peut prédire n’importe quoi en ayant l’air scientifique.

Et quand on dit “statistiques”, on entend déjà un chuchotement dans l’oreille qui nous rappelle à la prudence avec ces mots popularisés¹ par Mark Twain : “Il y a trois sortes de mensonges : les mensonges, les sacrés mensonges et les statistiques” ²

Mensonge ou erreur, peu importe, toujours est-il qu’il est facile de (se) tromper avec des chiffres. Et une de ces erreurs potentielles concerne les prédictions que l’on peut faire à partir des données passées. Pour faire de telles prédictions, bien souvent la méthode est la suivante : on observe les données passées puis on prolonge la tendance observée dans le futur.
Il est donc nécessaire de décider comment prolonger ces données : c’est ce que l’on appelle le modèle de régression. Et ce choix peut-être assez fallacieux. Pour illustrer ceci, reprenons l’exemple des performances athlétiques sur 100m.

Les Jeux-Olympiques de 2156 seront historiques !

Pour prédire l’avenir des perfomances athlétiques, une manière de faire consiste à analyser l’évolution des performances passés pour en déduire l’évolution future. On trace sur un graphique les données passées, on trace une courbe qui a l’air de coller aux données et on peut prédire le futur ! Facile !

C’est ce qui a, donc, été fait dans un article publié en 2004 dans la revue Nature et dont le titre peut se traduire par “Un sprint historique aux Jeux Olympiques de 2156 ?”³.
Les auteurs de l’étude ont collecté tous les temps des champions olympiques, masculins et féminins, du 100m (depuis 1900 pour les hommes et -seulement- depuis 1928 pour les femmes, et jusqu’en 2004 date de publication de l’article). Ces données ont ensuite été tracées sur un graphique et approchées par une courbe supposée représenter la tendance (voir ci dessous).

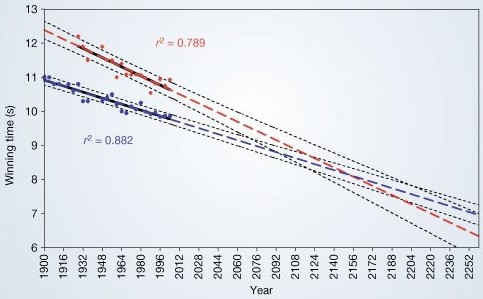
Tiré de « Momentous sprint at the 2156 Olympics? ».
Les points bleus et rouge correspondent aux données passées : temps du vainqueur (respectivement masculin et féminin) du 100m aux JO par année.
Les pointillés épais représentent la prédiction future et les pointillés fins représentent les intervalles de confiances.

Ainsi l’étude prédit qu’en 2100 le temps féminin du 100m olympique sera d’environ 8.9sec et le record masculin sera d’environ 8.5sec. Il prédit également qu’aux Jeux Olympiques de 2156, le temps de la course féminine pourrait, pour la première fois, passer en dessous de celui de la course masculine. En prenant en compte une marge d’erreur, ils prédisent plus exactement que ce dépassement devrait avoir lieu entre 2064 et 2788 (!)

Cette information a été reprise dans différents médias, par exemple dans Les Echos, sur RDS média sportif canadien, ou en anglais dans The Telegraph ou dans Manchester Eveningnews.

Quelques critiques générales peuvent être émises sur ce résultat, notamment sur la qualité des données qui sont assez peu nombreuses (elle ne comprend qu’une information tous les 4 ans; d’autres articles sur le sujet, considèrent les meilleures performances annuelles) et pas très consistantes (le chronométrage et le règlement ont évolué pendant cette période).
Mais la critique principale concerne le modèle de régression utilisé, autrement dit le choix des tracés bleu et rouge supposés approximer les données.

Préparez le chronométrage négatif

Les auteurs de l’étude proposent d’utiliser une régression linéaire, c’est-à-dire une ligne droite qui passe au plus près des données. Ce choix peut être tout à fait opportun si le phénomène étudié correspond effectivement à une évolution linéaire, au moins localement. Mais est-ce le cas ici ?

Avec le jeu de données qui est proposé, on s’aperçoit qu’une approximation avec une droite semble, en effet, assez bien coller aux données et c’est ce que remarquent les auteurs : “Une gamme de modèles a été testée, […]. Les modèles linéaires (proposés ici) ont donc été adoptés car ils représentaient l’option la plus simple.”⁴.
Il semble donc que localement, à l’échelle de quelques décennies l’utilisation d’un modèle linéaire pourrait être pertinent.

Mais vous avez certainement remarqué le piège ici : en suivant les prédictions de ce modèle, dans un futur lointain, on finit par tomber sur des résultats absurdes : les temps finiront par arriver à 0s (aux alentours de 2615 pour les femmes et de 2876 pour les hommes) puis négatif (les Jeux Olympiques de l’an 3000 devraient se gagner en -6,67sec pour les femmes et en -1,39sec pour les hommes !). Cette absurdité a d’ailleurs été pointée du doigt dans le numéro suivant de Nature par la chercheuse en biostatistiques Kenneth Rice ⁵Si l’on prolonge dans le passé, on remarque aussi que les premiers athlètes olympiques (vers -800) auraient couru le 100m en environ 41 secondes pour les hommes et 59 secondes pour les femme (s’il y en avait eu).
Pour comparaison, le record actuel du 100m des plus de 105 ans est de 34”50).

Dans ce cas, l’utilisation d’une régression linéaire pour modéliser l’évolution des performances en sprint sur le long terme n’est pas du tout adaptée et ne nous dit en réalité rien de très intéressant sur les Jeux Olympiques de 2156.
Une critique de l’utilisation d’un modèle linéaire dans cette situation a également été publiée dans le numéro suivant de Nature par Weia Reinboud ⁶ (qui n’est pas une scientifique mais une athlète).

Affutez son regard critique sur les modèles de régression

Un exercice intéressant consisterait à réfléchir, en premier lieu, aux propriétés que doit avoir un bon modèle de régression, autrement dit quelle forme devrait avoir la courbe pour approximer les données de manière cohérente.
Dans le cas de la prédiction des performances athlétiques futures, en voici trois :

Comme on l’a vu, le modèle ne devrait pas décroitre indéfiniment. La courbe d’approximation doit atteindre un minimum, on dit qu’elle doit avoir une borne inférieure.
Cette borne inférieure doit être strictement positive (évidemment, le temps de course ne peut être ni négatif, ni nul).⁷.
Si l’on souhaite étendre l’extrapolation dans le passé pour estimer le meilleur coureur à chaque époque, il faut également que le modèle aie une borne supérieure.

Ces contraintes théoriques étant établies (et possiblement d’autres), il est alors possible de choisir un modèle de régression qui les respecte. C’est ce qui est fait par exemple dans l’image ci-dessous extrait d’un autre article⁸ sur cette même problématique.

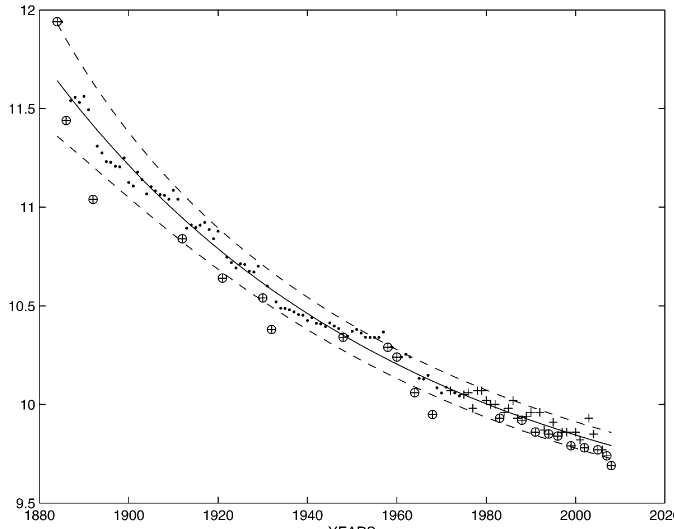
Meilleurs performances annuelles en 100m masculin connues (croix) ou estimées (points). Les cercles représentent les records. Tiré de Volf (2011).
Le modèle de régression utilisé ici (en trait plein) a une pente qui diminue dans le temps ce qui correspond bien à un phénomène qui a une borne inférieure.

Une fois le modèle choisi, les paramètres doivent être ajustés pour coller au plus près aux données existantes et pouvoir ainsi prédire la tendance future.
Cette recherche d’un modèle de régression adéquat qui est ensuite ajusté aux données illustre le fait que souvent, un résultat scientifique robuste se nourrit d’une part d’une cohérence théorique et d’autre part d’une conformité aux données factuelles.

Alors évidemment ici l’enjeu est minimal et si ces chercheurs anglais et leurs prédictions pour 2156 ont fait cette erreur, par maladresse ou pour le buzz, les conséquences sont négligeables.
Il peut, cependant, être utile de garder à l’esprit que faire des prédictions futures à partir de données passées est assez périlleux et peut amener à des conclusions hasardeuses. Si l’on se soustrait à une rigueur scientifique, aux méthodes mathématiques qui encadrent ce type d’estimation et que l’on confie au cerveau humain le soin de tracer les lignes qui prolongent des tendances, il y a fort à parier que l’on retrouvera les biais que l’on connait déjà par ailleurs.

Bonus

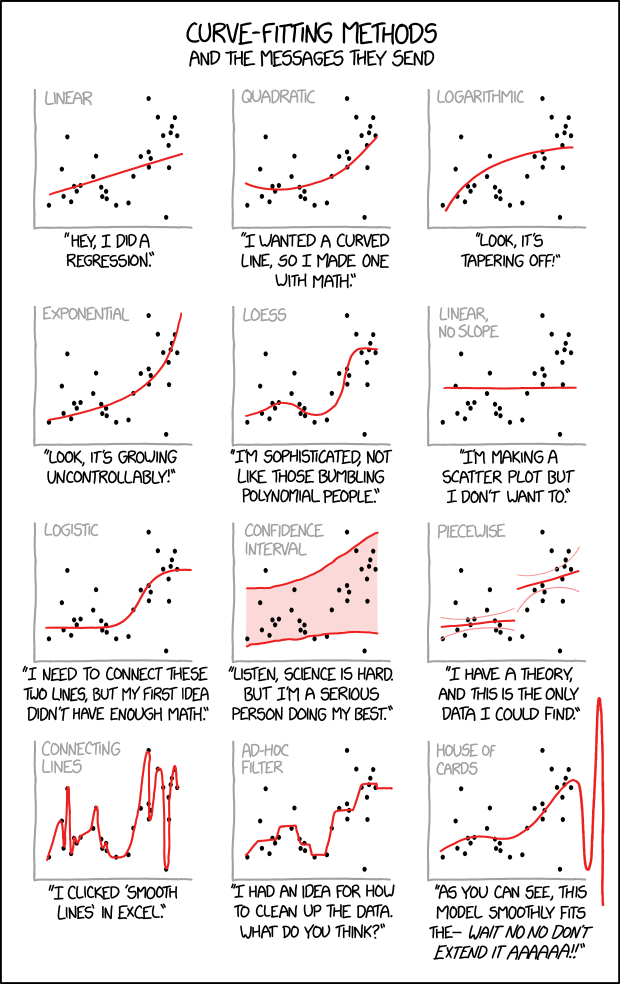
Et en bonus quelques planches supplémentaires de xkcd qui n’en finit pas d’extrapoler des données au delà du raisonnable.

La résolution de Google Earth augmentera-t-elle jusqu’à dépasser la résolution de la réalité elle-même ? (qui correspond à la longueur de planck)

En 2012, il prédisait que le nombre de personnages légo surpassera le nombre d’humains autour de 2020. En 2022, il semblerait que ce soit effectivement le cas⁹.

La fréquence d’utilisation du mot « durable » semble croitre exponentiellement depuis les années 50.
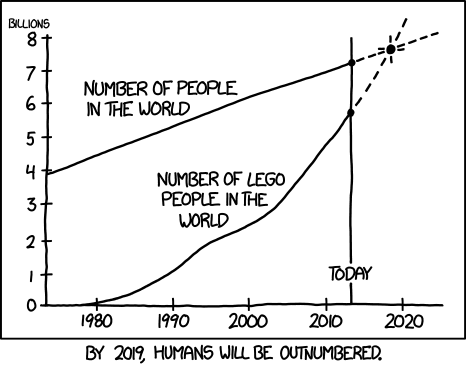
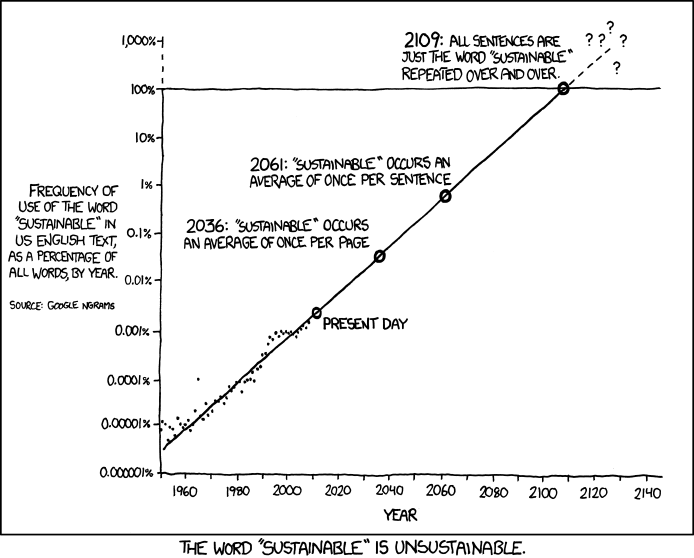
Il prédit qu’en 2036, le mot durable apparaitra en moyenne une fois par page; qu’en 2061 ce sera en moyenne une fois par phrase puis qu’en 2109, les phrases ne seront composées que du mot durable répété inlassablement. Au-delà de cette date, c’est « terra incognita ».

xkcd: Curve-Fitting — Les méthodes de régression et ce qu’elle signifie. Linéaire : « Hey, j’ai fait une regression »; Quadratique : « Je voulais une ligne courbe, du coup j’en ai tracé une mathématiquement »; Logarithmique : « Regardez, ça plafonne ! « ; Exponentielle : « Regardez, c’est hors de contrôle »; LOESS : « Je suis sophistiqué, pas comme ces empotés de polynomieux »; Constante : « Je fais un graphique, mais j’ai pas envie »; Logistique : » Il faut connecter ces deux lignes, mais ma première idée n’était pas assez mathématique ». Intervalle de confiance : « Bon, la science c’est compliqué. Mais je suis une personne consciencieuse qui fait de son mieux ». Par morceaux : « J’ai une théorie, et ce sont les seuls données que j’ai pu trouver ». Lignes connectées : « J’ai cliqué sur « Lisser les données » sur excel; Filtre ad-hoc « J’ai eu une idée pour nettoyer les données, tu en penses quoi ? »; Château de cartes : « Comme vous pouvez le voir, le modèle colle parfaitem- attends, non non ne prolonge paaaaaaas »

Vers une vision bayésienne de la zététique: Justifier et enrichir la démarche zététique à partir de la formule de Bayes

17 septembre 202011 octobre 2021 Alexandre Changenet et Nicolas Martin

Nicolas Martin, après avoir étudié les mathématiques appliquées à l’INSA Toulouse, a obtenu son doctorat en automatique au sein du GIPSA-lab et de l’université Grenoble Alpes. Il s’intéresse depuis plusieurs années à la zététique, l’esprit critique et leur transmission auprès du public. Depuis début 2020, Il publie des articles de vulgarisation scientifique et d’esprit critique sur le blog « Mon Œil ! »¹⁰Voici une de ses productions:

La zététique est un mouvement de pensée qui promeut l’utilisation de la pensée critique et de la méthode scientifique pour traiter efficacement le tsunami d’informations qui nous parvient chaque jour. Il semble néanmoins que cette démarche serait plus efficace encore si elle était soutenue par une vision bayésienne c’est-à-dire une approche qui prône l’usage des probabilités pour quantifier nos croyances. La démarche zététique est régulièrement le fruit de critiques : elle parait parfois dogmatique, parfois antipathique et parfois inapte à répondre à certains problèmes. Nous verrons dans cet article que le raisonnement bayésien soutient l’approche zététique et lui apporte un peu de nuance. Récemment, plusieurs travaux dans la communauté zététique sont allé dans ce sens, initiés principalement par Lê Nguyen Hoang (influencé par les travaux de Julia Galief écrivaine, conférencière et co-fondatrice du Center for Applied Rationality), avec son livre « La formule du savoir », sa série de vidéos sur le sujet ¹¹ et ses podcasts¹², l’approche bayésienne et ses apports à la zététique ont également été traités par Christophe Michel (animateur de la chaine Hygiène mentale)¹³, Nathan Uyttendaele (animateur de la chaine Chat Sceptique)¹⁴ ou encore Thibaud Giraud (animateur de la chaine Monsieur Phi)¹⁵. C’est dans ce mouvement que s’inscrit cet article dont l’objectif principal est de montrer comment le bayésianisme corrobore et enrichit certains outils zététiques.
Nous présenterons dans un premier temps quelques points critiques de la zététique qui motivent l’introduction d’un cadre bayésien. Nous introduirons ensuite succinctement le formalisme bayésien avant de présenter dans la dernière partie la contribution principale de cet article : la déduction de deux principes zététiques, rasoir d’Ockham et maxime de Hume, à partir de la formule de Bayes, formule sur laquelle se base l’approche bayésienne.
Cet article est loin de faire le tour de la question. Au contraire, comme son titre l’indique, le but ici est de fournir quelques arguments invitant à une réflexion plus poussée sur l’apport de l’approche bayésienne à la zététique.

Les limites de l’approche zététique

Il semble que l’approche zététique ait une mauvaise image de la part des croyant-e-s et des tenant-e-s des affirmations para-scientifiques¹⁶ mais pas seulement, certaines critiques viennent des zététiciens eux-mêmes¹⁷. Si certaines critiques peuvent être maladroites, d’autres en revanche nous paraissent pertinentes. Notons également que la plupart des critiques ne concerne pas la zététique dans son essence mais des écueils dans lesquelles il est facile de tomber. Nous proposons une liste de ces critiques ci-dessous. Nous verrons ensuite en quoi le bayésianisme peut répondre en partie à ces défaillances.

Des principes dogmatiques

Le rasoir d’Ockham, la maxime de Hume, la charge de la preuve, la valeur d’une preuve, l’impossibilité de prouver l’inexistence… Ces principes se posent parfois comme des dogmes de la zététique. Ce n’est pas un problème en soi puisque leur justification apparaît a posteriori : On se rend compte, en les utilisant, qu’effectivement on a tendance à se tromper moins souvent. En revanche, justifier a priori que ces principes sont cohérents, sont suffisants et nécessaires est une question plus complexe mais qui soutiendrait d’autant plus la démarche zététique.
En réalité, nous le verrons plus loin: le rasoir d’Ockham et la maxime de Hume peuvent se déduire de la formule de Bayes, formule dont on peut également justifier la cohérence.

De bons outils dans des mains maladroites

Carl Sagan dans The Fine art of Baloney Detection accompagne son texte de cette note appelant à la précaution : Like all tools, the baloney detection kit can be misused, applied out of context, or even employed as a rote alternative to thinking. But applied judiciously, it can make all the difference in the world — not least in evaluating our own arguments before we present them to others¹⁸. De même, dans son article critiquant la zététique, Sylvain Poirier fait remarquer : Ce n’est pas parce que beaucoup de principes zététiques affichés sont bons, que tout ce que disent les zététiciens est à croire sur parole. Si la zététique apporte un panel d’outils finement aiguisés, ils peuvent parfois être délétères lorsqu’ils sont utilisés sans un peu d’esprit critique.

Manque d’un formalisme mathématique

Le rasoir d’Ockham nous invite à “Privilégier l’hypothèse la plus parcimonieuse”. Mais comment quantifier la parcimonie d’une hypothèse ? Quelle métrique utiliser ?
La maxime de Hume, elle, stipule que “Une affirmation extraordinaire requiert des preuves extraordinaires”. Mais comment quantifier cette extraordinarité ? Et comment comparer l’extraordinarité d’une affirmation et l’extraordinarité des preuves ?
Bonne nouvelle, même si ces préceptes font office de principes généraux sans prétendre avoir une quelconque valeur quantitative, ils peuvent en fait être déduit de la formule de Bayes. Qui plus est, cette dernière leur donne un sens mathématique.

Manichéisme des arguments

Le curseur de vraisemblance¹⁹ invite à graduer la vraisemblance d’une affirmation sur une échelle continue entre 0% et 100%. Cette précaution apportée à notre jugement sur une théorie est bénéfique mais elle disparaît souvent quant on juge les preuves qui soutiennent la théorie : Il n’est pas rare d’entendre que tel argument est soit valide soit invalide; que le manque de rigueur d’un protocole invalide les résultats d’une expérience; que l’on peut jeter un discours puisque l’on y relève l’argument fallacieux n^∘21 ou le n^∘37²⁰. Il semble cependant que l’on perde de l’information en disqualifiant complètement une preuve imparfaite²¹. Dans son article critiquant la zététique, Sylvain Poirier écrit: Le fait qu’il y ait des impostures et des erreurs de toutes sortes à la base de certaines affirmations du paranormal ou d’autres choses par les uns ou les autres, ne signifie pas que tout y est faux ni que rien n’aurait pu être effectivement prouvé. Est-il bien raisonnable de considérer la valeur d’un argument comme binaire ? Il semble peu probable qu’un protocole soit parfait tout comme il est peu probable que tout soit à jeter. En replaçant la zététique dans un cadre probabiliste, on quitte le maigre²² {0;1} pour l’infiniment plus riche²³ [0,1].

Difficulté de conclure

“Est-il préférable pour la guérison d’une entorse de dormir avec un coussin bleu ou avec un coussin rouge ?”. Face à l’inexistence d’expériences randomisées en double aveugle avec groupe de contrôle, le zététicien doit-il s’enfuir laissant là son jugement suspendu ?
Devant bien des affirmations il semble que les outils de la zététique ne permettent pas de conclure. En particulier, on évoque souvent la hiérarchie suivante : une étude isolée est moins pertinente qu’une méta-analyse et une méta-analyse est moins pertinente que le consensus scientifique²⁴. Mais alors, que dire d’un sujet sur pour lequel il existe peu ou pas d’étude ? Que dire d’un sujet face à un faisceau d’indices réduit et/ou peu rigoureux ? L’approche bayésienne permet de prendre en compte des informations de toutes sortes afin de se faire une opinion.

Et donc ?

L’approche bayésienne offre une perspective qui répond en partie aux critiques sus-citées en permettant de :

Quantifier la validité d’une information et la probabilité d’une affirmation.
Corroborer certains des principes dogmatiques de la zététique évoqués ci-dessus
Replacer le discours zététique dans un langage probabiliste : Utiliser une formule comme « Il est très improbable que X » plutôt qu’un plus catégorique « À l’heure actuelle, il n’y a aucune preuve de X » rend le discours plus humble et plus propice à un échange bienveillant²⁵.

Les apports du bayésianisme

Pour ne pas alourdir l’article la présentation du bayésianisme est assez minimaliste. Le lecteur curieux est invité à se référer aux références données dans l’introduction.

De la formule de Bayes

Le bayésianisme se base sur la formule de Bayes dont il tire son nom. La manière la plus simple d’écrire cette formule est la suivante

(1) $\begin{equation*}\Prob{A|B} = \frac{\Prob{A}\Prob{B|A}}{\Prob{B}}\end{equation*}$

Les termes ℙ(A|B) et ℙ(B|A) sont des probabilités conditionnelles et se lisent respectivement “Probabilité de A sachant B” et “Probabilité de B sachant A”. La formule de Bayes permet donc simplement de lier les deux probabilités conditionnelles.

Exemple : On considère un lancer de dé, et on cherche à savoir quelle est la probabilité que le dé soit tombé sur 6 sachant que le dé est tombé sur un chiffre pair. On parle donc de probabilité conditionnelle car on cherche la probabilité d’un évènement en connaissant des informations partielles sur cet évènement.
Dans la formule de Bayes 1, on remplace A et B respectivement par “Faire un 6” et “Faire un nombre pair”. On va donc pouvoir calculer ℙ(A|B), la probabilité de “Faire un 6” sachant qu’on a “Fait un nombre pair”, ce qui est bien ce qu’on recherche. On obtient :

$\small \Prob{\text{Faire un 6}|\text{Faire un nombre pair}} = \frac{\Prob{\text{Faire un 6}}\Prob{\text{Faire un nombre pair}|\text{Faire un 6}}}{\Prob{\text{Faire un nombre pair}}}$

Ce qui se lit : la probabilité que j’ai fait un 6 sachant que j’ai fait un nombre pair est égale à la probabilité de faire un 6 (égale à 1/6) multipliée par la probabilité de faire un nombre pair sachant que j’ai fait un 6 (égale à 1) divisée par la probabilité de faire un nombre pair (égale à 1/2). Ce qui donne :

$\begin{equation*} \Prob{\text{Faire un 6}|\text{Faire un nombre pair}} = \frac{1/6 \times 1}{1/2} = 1/3 \end{equation*}$

que l’on peut facilement vérifier.

À la formule du savoir

Initialement cette formule est un simple outil de calcul de probabilité conditionnelle relativement simple, et c’est ainsi qu’elle est enseignée aux étudiants. Cependant, réinterprétée, notamment par Pierre-Simon de Laplace, elle est devenue un profond principe épistémologique, que certains considèrent comme la formule ultime du savoir²⁶ fondant ainsi le bayésianisme.
Comme nous le verrons, la formule de Bayes permet de calculer la vraisemblance d’une affirmation en fonction de la vraisemblance a priori de cette affirmation et d’une nouvelle information. Autrement dit, elle permet de mettre à jour nos croyances en fonction des preuves que l’on peut rencontrer : témoignage, étude scientifique, reportage TV, article de presse, …
Le théorème dit de Cox-Jaynes permet même de s’assurer que c’est la bonne manière de faire. Ce théorème montre que la logique bayésienne découle de certains prérequis naturels²⁷ et qu’elle est donc indispensable pour manipuler raisonnablement de l’information.

La théorie des probabilités n’est rien d’autre que le sens commun qui fait calcul — Pierre-Simon de Laplace

Retour à la zététique

Nous voilà rendus bien loin des préoccupations zététiques. Mais en apportant une légère modification à la formule de Bayes ci-dessus nous allons y revenir. Changeons tout simplement le A dans la formule par affirmation, et le B par preuve²⁸. Et voilà, nous avons un outil mathématique puissant pour estimer la vraisemblance d’une affirmation à partir de preuves (que ce soit des témoignages, des études, des arguments, …).
Mise en pratique :

$\begin{equation*} \Prob{\text{Affirmation}|\text{Preuve}} = \frac{\Prob{\text{Affirmation}}\Prob{\text{Preuve}|\text{Affirmation}}}{\Prob{\text{Preuve}}} \end{equation*}$

$\Prob{\text{Affirmation}|\text{Preuve}}$ est ce que l’on cherche à évaluer: la vraisemblance d’une affirmation à partir de preuves. Plus précisément, on cherche à calculer l’évolution de la confiance à accorder en une affirmation lorsque une nouvelle preuve est disponible. Cette quantité est aussi appelée probabilité a posteriori puisqu’elle correspond à la vraisemblance de l’affirmation après avoir pris en compte la preuve.
Par opposition, $\Prob{\text{Affirmation}}$ représente la probabilité a priori. C’est à dire la vraisemblance de l’affirmation avant de prendre en compte la preuve. C’est un des principes fondamentaux du bayésianisme : notre croyance en une affirmation évolue sans cesse en fonction des nouvelles preuves qui nous parviennent.
$\Prob{\text{Preuve}}$ est la probabilité a priori d’observer la preuve. Insistons: ces deux dernières probabilités ( $\Prob{\text{Affirmation}}$ et $\Prob{\text{Preuve}}$ ) sont calculées dans l’état initial des connaissances, c’est-à-dire sans prendre en compte la nouvelle preuve.
Enfin, la formule de Bayes nous dit que pour trouver $\Prob{\text{Affirmation}|\text{Preuve}}$ , il nous faut, de plus, la probabilité d’observer cette preuve si l’affirmation est vraie. Cette probabilité est notée: $\Prob{\text{Preuve}|\text{Affirmation}}$ , et est également appelée « fonction de vraisemblance », ou simplement « vraisemblance ».
On peut alors calculer $\Prob{\text{Affirmation}|\text{Preuve}}$ , la probabilité a posteriori de l’affirmation, c’est-à-dire la confiance à accorder en l’affirmation²⁹ une fois pris en compte les nouveaux éléments de preuve relativement aux connaissances préalables. D’une certaine manière, la formule décrit comment utiliser raisonnablement le curseur de vraisemblance connu des zététiciens.
La dépendance aux connaissances initiales peut sembler gênante puisqu’elle est subjective et risque de faire aboutir deux personnes à des conclusions différentes. Cependant la formule de Bayes assure qu’avec un nombre de preuves suffisant les probabilités a posteriori convergent vers une même valeur quelque soit la probabilité a priori.
Avec ces notations, une affirmation est très probable si $\Prob{\text{Affirmation}}$ est proche de 1 et inversement très improbable si $\Prob{\text{Affirmation}}$ est proche de 0. De même, $\Prob{\text{Preuve}}$ proche de 0 correspond à une preuve très improbable dans le cadre initial de nos connaissance donc à une preuve que l’on peut qualifier d’extraordinaire (par ex. « Il a neigé en Août »), alors que $\Prob{\text{Preuve}}$ proche de 1 est une preuve banale c’est à dire une information à laquelle on s’attend (par ex. « Il a neigé en Janvier »).
Avant de voir les avantages du cadre bayésien dans la démarche zététique, voyons un exemple rapide d’utilisation de la formule de Bayes dans un cadre zététique.

Exemple : La maison de mes grand-parents est connue pour être hantée, notamment la vieille chambre du fond. Armé de tout mon courage et de mes solides outils zététique je vais la visiter. J’émets deux hypothèses :

Affirmation Affirmation $A_1$ : « Il y a des oiseaux dans les combles à l’origine des phénomènes ». J’y attribue une probabilité de $\Prob{A_1} = 0.9$ .
Affirmation $A_2$ : « Il n’y a pas d’oiseau dans les combles et la maison est vraiment hantée ». J’y attribue une probabilité $\Prob{A_2} = 0.1$ ça paraît fou mais la croyance est tenace dans la famille et dans le village.

En arrivant dans la chambre, et non loin en dessous d’une ouverture dans le plafond qui donne accès aux combles, je vois une plume d’oiseau. Voilà ma nouvelle preuve $P$ qui va me permettre de mettre à jour mes croyances. On peut estimer la probabilité de trouver une plume là sachant qu’il y a des oiseaux dans les combles $\Prob{P|A_1} = 0.05$ : c’est commun de trouver des plumes mais encore fallait il qu’elle passe par cette petite ouverture. De même on estime la probabilité de trouver une plume sachant qu’il n’y a pas d’oiseau $\Prob{P|A_2} = 0.0001$ : c’est très peu probable, il aurait fallu que quelqu’un l’amène ici. On peut enfin calculer la probabilité de trouver une plume $\Prob{P}$ grâce à la formule suivante³⁰: $\Prob{P} = \Prob{P|A_1}\times\Prob{A_1} + \Prob{P|A_2}\times\Prob{A_2} = 0.04501$ .
On peut maintenant appliquer la formule de bayes pour $A_1$ et $A_2$ .

$\begin{equation*} \begin{split} \Prob{A_1 | P}& = \frac{\Prob{A_1}\Prob{P|A_1}}{\Prob{P}}\\ \Prob{A_1 | P} & = \frac{0.9 \times 0.05}{0.04501}\\ \Prob{A_1 | P} & \approx 0.9998 \end{split} \end{equation*}$

$\begin{equation*} \begin{split} \Prob{A_2 | P} & = \frac{\Prob{A_2}\Prob{P|A_2}}{\Prob{P}}\\ \Prob{A_2 | P} & = \frac{0.1 \times 0.0001}{0.04501}\\ \Prob{A_2 | P} & \approx 0.0002 \end{split} \end{equation*}$

Après mise à jour des vraisemblances j’attribue donc une probabilité de $99,98\%$ pour l’affirmation $A_1$ et $0,02\%$ pour l’affirmation $A_2$ .
Évidemment faire une telle analyse chiffrée n’est pas possible au quotidien et ce n’est même pas utile à vrai dire. Mais il est très bénéfique d’adopter une pensée bayésienne en prenant l’habitude de mettre à jour la vraisemblance de nos croyances et en musclant notre intuition bayésienne³¹.

On peut maintenant voir en quoi cette approche permet de répondre aux critiques formulées dans la section précédente :

Elle peut être utilisée pour justifier les principes a priori arbitraires de la zététique. Puisque le théorème de Cox-Jaynes montre que l’approche bayésienne est la seule cohérente, alors démontrer les principes zététiques par la formule de Bayes justifierait leur pertinence. C’est ce que nous ferons dans la dernière section pour deux de ces principes.
Puisque dans l’approche bayésienne tout est exprimé en fonction de probabilité on évite la binarité et la rigidité que peut prendre parfois le discours zététique.
Comme nous le verrons dans la dernière section, en plus de justifier le rasoir d’Ockham et la maxime de Hume, l’approche bayésienne apporte un cadre mathématique qui permet de quantifier ce qu’on entend par « l’hypothèse la plus parcimonieuse » ou une « affirmation extraordinaire ».
Alors que la zététique requiert parfois une étude approfondie d’un sujet pour obtenir une conclusion, l’approche bayésienne permet toujours d’attribuer une vraisemblance à l’affirmation quel que soit la quantité d’information dont on dispose.

Les outils zététiques dans une main bayésienne

Les deux premières parties ont permis de montrer ce que le bayésianisme peut apporter à la zététique et s’alignent avec des travaux pré-existants (notamment ceux de Christophe Michel présenté dans l’introduction). Cette dernière partie est une contribution plus personnelle (et plus technique aussi peut-être) et montre comment le cadre bayésien permet de justifier deux principes fondamentaux de la zététique : le rasoir d’Ockham et la maxime de Hume répondant ainsi partiellement³² à la première critique formulée.

Rasoir d’Ockham

Quand on est confronté à plusieurs affirmations expliquant un même phénomène, le rasoir d’Ockham nous invite à privilégier l’affirmation la plus parcimonieuse. C’est à dire, l’affirmation qui requiert les hypothèses les moins coûteuses intellectuellement. Cependant, la signification de parcimonie ne va pas toujours de soi en l’absence de quantifications.
Voyons ce que l’approche bayésienne peut en dire. Admettons que l’on ait trois affirmations $A_1$ , $A_2$ et $A_3$ pour expliquer la même preuve P. les formules de Bayes s’écrivent alors :

$\begin{equation*} \begin{split} \Prob{A_1|P} & = \frac{\Prob{A_1}\Prob{P|A_1}}{\Prob{P}} \\ \Prob{A_2|P} & = \frac{\Prob{A_2}\Prob{P|A_2}}{\Prob{P}} \\ \Prob{A_3|P} & = \frac{\Prob{A_3}\Prob{P|A_3}}{\Prob{P}} \\ \end{split} \end{equation*}$

Chercher l’affirmation à privilégier revient à chercher l’affirmation la plus probable au vu de la preuve, donc la plus grande de ces trois probabilités. En multipliant toutes ces quantités par $\Prob{P}$ , on cherche donc l’affirmation maximisant $\Prob{A_i} \Prob{P|A_i}$ .
Ce qui peut se lire : Probabilité de l’affirmation $A_i$ multipliée par la probabilité d’observer la preuve $P$ sachant que l’affirmation $A_i$ est vraie. La formule de Bayes nous dit donc comment interpréter le terme « plus parcimonieux » du rasoir d’Ockham. Ce n’est donc pas simplement l’affirmation la plus probable qu’il faut privilégier, c’est à dire $\Prob{A_i}$ , mais bien le produit de cette probabilité avec la probabilité d’observer $P$ sachant que $A_i$ (l’exemple à venir rendra la nuance plus claire). On peut en déduire une nouvelle formulation pour le rasoir d’Ockham:

Rasoir d’Ockham bayésien :L’hypothèse maximisant $\Prob{A_i} \Prob{P|A_i}$ doit être privilégiée. C’est à dire l’hypothèse maximisant le produit de la probabilité de $A_i$ et de la probabilité d’observer la preuve $P$ sachant $A_i$ .

Cela peut sembler être une subtilité mais l’exemple suivant montre la différence induite par ce changement.

Exemple : Monsieur M. met dans une boite un chat et un souris. Dix secondes après il rouvre la boîte et la souris a totalement disparu. On peut émettre plusieurs affirmations :

$A_1$ = Le chat a mangé la souris
$A_2$ = La souris est passé dans une dimension différente pour échapper au chat
$A_3$ = Monsieur M. est magicien

Usons de notre rasoir d’Ockham bayésien pour voir quelle affirmation privilégier. On considère les probabilités a priori des affirmations suivantes : $\Prob{A_1} = 0.8$ : Les chats aiment manger des souris;
$\Prob{A_2} = 0.0000001$ : Je n’ai pas connaissance de souris ayant une telle capacité;
$\Prob{A_3} = 0.1$ : Je ne connais pas bien cette personne, mais il n’est pas impossible que ce soit un tour de magie.

Si on s’intéresse au curseur de vraisemblance utilisé classiquement en zététique, nous pourrions penser qu’il ne faut considérer que la probabilité a priori $\Prob{A_i}$ de ces affirmations. Ainsi il semblerait que l’affirmation $A_1$ soit à privilégier.
Considérons désormais la seconde partie du calcul uniquement (celle qui prend en compte la probabilité d’observer la donnée si l’affirmation est vraie), et que nous appelons la fonction de vraisemblance ou simplement vraisemblance. La donnée en l’occurrence est la révélation du contenu de la boite 10 secondes plus tard sans souris. On a alors par exemple : $\Prob{P | A_1} = 0.1$ : Seulement 10 secondes pour manger une souris et ne laisser aucune trace… ça me parait suspect; $\Prob{P | A_2} = 0.999$ : Si la souris avait un tel pouvoir elle aurait en effet sûrement disparu; $\Prob{P | A_3} = 0.95$ : Si Monsieur M. est magicien alors il est très probable que la disparition de la souris soit son tour de magie. En ne regardant que cette « vraisemblance », c’est alors le voyage inter-dimensionnel qui est à privilégier.

Dans un cadre bayésien, c’est la probabilité a posteriori que nous devrions regarder. C’est le produit des deux quantités précédentes³³. On trouve alors :

$\begin{equation*} \begin{split} \Prob{A_1}\Prob{P|A_1} &= 0.8 \times 0.1 = 0.08 \\ \Prob{A_2}\Prob{P|A_2} &= 0.0000001 \times 0.999 = 0.0000000999 \\ \Prob{A_3}\Prob{P|A_3} &= 0.1 \times 0.95 = 0.095 \end{split} \end{equation*}$

Au final, l’hypothèse à privilégier est que Monsieur M. est magicien…
Dans l’utilisation classique du rasoir d’Ockham cette précision n’est pas faite et le terme « affirmation la plus parcimonieuse » peut prêter à confusion.
On peut donc résumer le calcul ainsi :

$\begin{equation*} \begin{split} & \text{Probabilité a posteriori (ou \textit{posterior})} = \\ & \text{curseur de vraisemblance non bayésien (ou\textit{ prior})} \times \text{vraisemblance} \end{split} \end{equation*}$

Les termes posterior et prior sont communément utilisés dans le cadre bayésien comme indiqué dans la formule ci-dessus.

Maxime de Hume

Également appelée standard de Sagan, ou de Truzzi, ou de De Laplace³⁴, cette maxime postule que « Une affirmation extraordinaire requiert une preuve extraordinaire ».
Ici encore, nous allons voir que le cadre bayésien permet de retrouver et de préciser cette affirmation. Reprenons à nouveau la formule de Bayes :

(2) $\begin{equation*}\Prob{\text{Affirmation}|\text{Preuve}} = \frac{\Prob{\text{Affirmation}}\Prob{\text{Preuve}|\text{Affirmation}}}{\Prob{\text{Preuve}}}\end{equation*}$

Comme dit précédemment une affirmation est dite extraordinaire si elle est a priori très peu probable. Une telle affirmation vérifie donc $\Prob{\text{Affirmation}} = \epsilon$ , où $\epsilon$ est une quantité très petite. Pour que cette affirmation, une fois pris en compte le nouvel élément de preuve, soit vraisemblable, il faut donc une preuve qui mène à $\Prob{\text{Affirmation}|\text{Preuve}} \approx1$ . On peut montrer que cette condition³⁵ implique la relation suivante:

(3) $\begin{equation*}\Prob{\text{Preuve}} \ll \Prob{\text{Preuve}|\text{Affirmation}}\end{equation*}$

Ainsi pour qu’une affirmation a priori extraordinaire devienne vraisemblable il faut donc que la probabilité d’observer la preuve soit beaucoup plus petite que la probabilité d’observer la preuve sachant l’affirmation (nous verrons un exemple plus loin). La formule de Hume se déduit simplement en observant que comme toute probabilité est inférieur ou égale à $1$ on a $\Prob{\text{Preuve}|\text{Affirmation}} \leq 1$ et donc

(4) $\begin{equation*}\Prob{\text{Preuve}} \ll 1\end{equation*}$

Ainsi la probabilité d’observer la preuve doit être très petite. En d’autres terme, la preuve doit être extraordinaire³⁶ ! Ainsi, la formule de Bayes permet bien de démontrer la maxime de Hume.
Cependant la formule (3) en dit un petit peu plus :

la condition, $\Prob{\text{Preuve}} \ll 1$ n’est pas suffisante ! Il faut également que $\Prob{\text{Preuve}} \ll \Prob{\text{Preuve}|\text{Affirmation}}$ et donc que la probabilité d’observer la preuve sachant l’affirmation ne soit pas trop petite ! C’est à dire qu’il faut que la preuve soit ordinaire si l’affirmation est vraie : $\Prob{\text{Preuve}|\text{Affirmation}} \equiv 1$ .
On peut en déduire une nouvelle formulation pour la maxime de Hume.

Maxime de Hume bayésienne : Une affirmation extraordinaire requiert une preuve extraordinaire. Mais il faut aussi que la preuve soit ordinaire si l’affirmation est vraie.

Exemple :

Considérons l’affirmation $A =$ « les licornes existent » que l’on peut qualifier d’extraordinaire. J’y octroie a priori une probabilité de un sur un milliard : $\Prob{A} = 10^{-9}$ Pour que cette affirmation paraisse crédible, il faut donc observer une preuve $P$ vérifiant $\Prob{P} \ll \Prob{\text{P}|\text{A}}$ .
Considérons par exemple la preuve $P_1$ : « Quelqu’un a vu de loin une silhouette de cheval avec une corne sur le front ». Ce n’est pas une preuve si extraordinaire : il a pu se tromper, c’était peut-être une installation artistique, des petits malins ont pu attacher un postiche ou il a menti. J’estime la probabilité d’observer cela à un sur mille. On a donc $\Prob{P_1} = 0.001$ . En revanche, il est clair que la probabilité que quelqu’un ait vu de loin une silhouette de cheval avec une corne sur le front sachant que les licornes existent est très élevée : $P(P_1 | A) \approx 1$ .
On peut maintenant appliquer la formule de Bayes pour mettre à jour ma croyance en $A$ sachant $P_1$ :

$\begin{align*} \Prob{A|P_1} & = \frac{\Prob{A}\Prob{P_1|A}}{\Prob{P_1}} = \frac{10^{-9} \times 1}{0.001} = 10^{-6} \end{align*}$

Après cette preuve, j’octroie à l’existence des licornes une crédence de un sur un million. Cette preuve satisfaisait donc un seul des deux critères de la maxime de Hume bayésienne : elle est ordinaire si l’affirmation est vraie mais elle n’est pas extraordinaire en soi.
Au contraire prenons une autre preuve $P_2$ qui a une chance sur un milliard d’être observée : « J’ai fait 30 piles de suite ». La preuve est bien extraordinaire $\Prob{P_2} \approx 10^{-9}$ . Mais là encore la preuve ne satisfait qu’un seul des deux critères de la maxime de Hume baysésienne : elle est extraordinaire mais elle n’est pas ordinaire si l’affirmation est vraie. En effet, ici les deux évènements sont décorrélés : l’existence de licorne ne rend pas plus ordinaire une suite de 30 piles $P(P_2 | A) \approx 10^{-9}$ . Ça ne suffit donc pas à me convaincre. En l’occurrence la formule de Bayes donne:

$\begin{align*} \Prob{A|P_2} & = \frac{\Prob{A}\Prob{P_2|A}}{\Prob{P_2}} = \frac{10^{-9} \times 10^{-9}}{10^{-9}} = 10^{-9} \end{align*}$

Ce deuxième cas est caricatural mais il soulève une erreur de logique : se contenter d’une preuve extraordinaire sans vérifier que cette preuve est beaucoup plus probable dans l’affirmation qu’elle cherche à valider.
Enfin une preuve satisfaisante pourrait donc être $P_3$ un article scientifique corroboré par plusieurs chercheurs et fournissant suffisamment d’informations sur l’existence de licornes et étayé par des vidéos et des photos. Une telle preuve serait tout à fait extraordinaire en soi (estimée pour l’exemple à une chance sur 800 millions) et totalement ordinaire si l’affirmation est vraie (estimée ici à $0.99\%$ ). La formule de Bayes donne alors :

$\begin{align*} \Prob{A|P_3} & = \frac{\Prob{A}\Prob{P_3|A}}{\Prob{P_3}} = \frac{10^{-9} \times 0.99}{1.25*10^{-9}} = 0.792 \end{align*}$

Ma crédence en l’existence des licornes est donc passé à environ $80\%$ .

Conclusion

Voilà donc quelques idées sur la complémentarité entre bayésianisme et zététique. Nous avons montré d’abord quelques écueils possible de la démarche zététique et comment le cadre bayésien permets en partie d’y répondre. Dans une dernière partie nous avons montré comment la formule de Bayes permet de retrouver et préciser deux principes de la zététique : le rasoir d’Ockham et la maxime de Hume.
Bien d’autres pièces restent à ajouter au puzzle afin d’obtenir un paradigme plus solide. Quid des autres principes de la zététique ? Des biais cognitifs et des sophismes ? Quid de la charge de la preuve ? Est-ce que la perspective bayésienne permet d’en dire quelque chose, voire d’enrichir ces concepts ? Néanmoins, à l’avenir, si votre recette zététique semble mécontenter votre auditoire, essayer d’y rajouter une pincée de bayésianisme pour la rendre plus légère.

Le jugement majoritaire et ses alternatives

11 juin 202011 juin 2020 Raul Magni-Berton

Le système électoral français est critiqué pour de très bonnes raisons. Parmi les alternatives, celle qui connait le plus de succès auprès des citoyens est le jugement majoritaire. Cependant, ce système a aussi des défauts. Cet article vise à illustrer comment débattre des systèmes électoraux
et à montrer que d’autres alternatives – comme le vote par approbation – mériteraient d’être davantage discutées dans un public plus large que les chercheurs spécialistes.

Critiquer un système électoral est facile puisqu’en matière de décompte de voix, aucune méthode n’est parfaite. Si la critique se borne à identifier les défauts d’un système – il y en a toujours plus d’un – et le délégitimer en vertu de ceux-ci, tout système est critiquable. Toutefois, il existe des systèmes électoraux avec moins de défauts que d’autres, ou avec des défauts qui ont des conséquences moins graves. Et c’est sur ce point que la discussion devient intéressante. Parmi les défauts existants, quels sont ceux qui sont rédhibitoires ?

La France dispose d’un système électoral uninominal à deux tours. Ce système a de nombreux problèmes si bien que deux chercheurs CNRS Michel Balinski et Rida Laraki ont proposé, au début des années 2000, un système alternatif : le jugement majoritaire ³⁷. Ce système s’est diffusée comme une traînée de poudre dans les cercles politiques et militants où on lui a attribué de nombreuses qualités. Seulement voilà : ce système pose lui aussi de sérieux problèmes. Je reviens ici sur une controverse bien informée, lancée par la publication en 2019 dans la Revue Economique, d’une analyse critique du jugement majoritaire par Jean-François Laslier ³⁸, critique face à laquelle Michel Balinski, décédé depuis, a réagi ³⁹. Laslier est par ailleurs un défenseur du système du vote « par approbation » qui récolte aussi mon soutien.

L’occasion est donc parfaite pour comparer ces trois systèmes sur un des défauts les plus problématiques à mon sens : l’absence de monotonie. Un système est monotone si, quand le soutien en faveur d’un candidat élu augmente, celui-ci reste élu. Et, symétriquement, si le soutien en faveur d’un candidat non élu diminue, alors celui-ci n’est toujours pas élu.

Compte tenu de l’existence d’une longue liste de critères pour évaluer un système électoral⁴⁰, pourquoi l’absence de monotonie est si regrettable ? Parce que non seulement elle offre une capacité de manipuler les résultats électoraux mais surtout, comme on le verra plus bas, elle incite parfois les élus à nuire à certains électeurs, voire à délibérément mal faire leur travail afin de gagner les prochaines élections. Or, si on élit des gens à des intervalles réguliers, c’est pour qu’ils soient incités à nous satisfaire et pour les soumettre à notre contrôle. Si, au lieu de cela, notre mode de scrutin les incite à nous déplaire pour gagner les élections, l’utilité des élections disparaît.

Analysons trois modes de scrutins – le système à deux tours, le jugement majoritaire et le vote par approbation – par rapport au problème de l’absence de monotonie. Les choses étant vite techniques, le raisonnement va être limité aux élections présidentielles, et ne prendra pas en compte les votes blancs et les abstentions.

Le système à deux tours

Avec notre système actuel, chacun vote pour un candidat, les deux premiers se qualifient au second tour où celui qui récolte le plus de voix gagne.

Revenons dans le temps, à l’élection présidentielle de 2017. Prenons en compte, pour plus de simplicité, seulement les trois candidats qui ont eu le plus de voix au premier tour : Emmanuel Macron, Marine Le Pen et François Fillon.

Pour chaque candidat, les électeurs se répartissent en deux catégories différentes, ce qui donne six configurations possibles (Figure 1). En effet, parmi ceux qui choisissent de voter Macron, certains (1) préfèrent ensuite Fillon à Le Pen alors que d’autres (2) préfèrent Le Pen à Fillon. De même, parmi les électeurs ayant voté pour Fillon, certains (3) préfèrent Macron à Le Pen, alors que d’autres (4) préfèrent Le Pen à Macron. Enfin, les électeurs de Le Pen peuvent préférer Fillon à Macron (5) et d’autres Macron à Fillon (6).

Supposons que 21% des électeurs préfèrent, par ordre, Macron/Fillon/Le Pen, et seulement 3% préfèrent Macron/Le Pen/Fillon. La somme des deux, permet à Macron d’obtenir 24% au premier tour (colonne à gauche). Conformément à ce qui est arrivé en 2017, Fillon a obtenu 20% (nous supposons que ¾ de ses électeurs préfèrent Macron à Le Pen, soit 15% des votes) et Le Pen a eu 21% (parmi ceux-ci,17% préférant Fillon à Macron, et 4% Macron à Fillon).

Le second tour voit donc s’affronter Macron contre Le Pen. Compte tenu de nos chiffres, qui excluent les autres candidats, Macron ajoute à ses 24%, les 15% qui avaient voté pour Fillon et qui préfèrent tout de même Macron à Le Pen (colonne de gauche de la figure de droite). Cela fait 39% en tout. Le Pen, elle, n’obtiendra que 26%, en récupérant 5% dans l’électorat de Fillon. Macron gagne donc haut la main.

Entrons maintenant dans la science-fiction. Nous sommes en 2022. Supposons – et cela nécessite quelques efforts j’en conviens – qu’Emmanuel Macron ait bien gouverné, si bien que tous ses électeurs continuent à voter pour lui, mais, de surcroît, il arrive à séduire 2% d’électeurs qui lui préféraient Le Pen en 2017. Hormis ces 2%, tous les autres électeurs gardent la même opinion qu’en 2017 (Figure 2). A priori une bonne affaire pour Macron : il avait déjà gagné avec 2% d’électeurs en moins, maintenant qu’il garde son électorat tout en l’élargissant, il devrait triompher sans peine.

Calculez l’issue du vote vous-mêmes à partir de la figure 2. A cause de la perte de 2% des électeurs, Le Pen n’est plus qualifié au second tour, au profit de Fillon. Fillon obtiendra alors 37% au second tour (grâce au soutien massif de l’électorat Le Pen), alors que Macron s’arrêtera à 28%. Fillon sera donc président (Figure 3).

En quoi est-ce gênant ? D’abord pour le bon sens, car dans notre fiction, Macron ayant bien gouverné, il a non seulement continué à satisfaire son électorat de 2017, mais il a aussi séduit des électeurs supplémentaires. Mais c’est surtout politiquement gênant, puisque Macron n’a aucun intérêt à gagner des voix parmi l’électorat du Rassemblement National. Il doit en effet viser un second tour contre Le Pen. Il va donc essayer de séduire l’électorat Fillon et de déplaire à l’électorat Le Pen. Sachant que le premier est constitué de cadres supérieurs et de professions libérales, alors que le second est largement composé d’ouvriers et d’artisans, Macron n’a pas d’autre choix : plaire aux premiers, déplaire aux seconds. S’il veut gagner, il doit mettre en place une politique inégalitaire. Ses choix sont donc partiellement guidés par les contraintes de notre système électoral.

Le jugement majoritaire

Est-ce que ce le jugement majoritaire peut résoudre cet important problème? Le jugement majoritaire est un mode de scrutin par évaluation qui conduit à l’élection du candidat ayant la meilleure « évaluation médiane ». Autrement dit, si une personne pense que je suis bon cuisinier, une autre pense que je suis plutôt moyen et une dernière pense que je suis carrément mauvais, mon évaluation médiane est celle du milieu : « moyen ».

Par conséquent, il semble impossible qu’un candidat qui avait gagné auparavant, puisse perdre en ayant amélioré ses évaluations. Cela est cependant possible si l’électorat évolue (s’il augmente ou, au contraire, s’il se réduit). Autrement dit, cela peut se produire si entre 2017 et 2022 quelques jeunes obtiennent le droit de vote ou si des personnes âgées meurent.

Postulons donc deux candidats, Macron et Le Pen et neuf électeurs (on peut multiplier par cinq millions, si on veut s’approcher de la taille de l’électorat français). Le jugement majoritaire détermine le gagnant en cherchant l’évaluation du 5^ème électeur, l’électeur médian. D’après la figure 4 (les deux colonnes de gauche), selon cet électeur, Macron est « assez bon », alors que Le Pen est « acceptable ». Macron sera donc président.

La partie droite de la Figure 3 analyse la situation cinq ans plus tard, en 2022. Supposons d’abord que chaque électeur vote comme 2017. Supposons également que personne ne soit mort, mais, par contre, deux adolescents aient atteint la majorité et puissent maintenant voter. La jeunesse (dans ce jeu fictionnel) adore Macron : les deux le trouvent « excellent », alors qu’ils considèrent Le Pen simplement « bonne ». A priori, donc, tout va bien pour Macron qui avait déjà gagné sans les deux jeunes en 2017.

Mais hélas, après calcul, il va être déçu. Les votants sont maintenant onze, par conséquent l’évaluation médiane est celle du 6^èmeélecteur. Comptez : le sixième considère Macron « assez bon » et Le Pen « bon ». C’est donc Le Pen qui est élue présidente, grâce à ces deux jeunes qui ont évalué de façon enthousiaste le bilan de Macron.

Pour gagner, Macron aurait dû se débrouiller pour que les deux jeunes considèrent Le Pen au mieux acceptable, quitte à être lui-même considéré médiocre ou à rejeter. En fait, avec le jugement majoritaire, Macron n’aurait aucun intérêt à plaire aux deux jeunes car même si ces derniers le détestent, cela ne lui coutera rien lors des élections. Il a en revanche intérêt à ce que les jeunes notent moyennement Le Pen. Au lieu de gouverner le mieux possible, de faire des bonnes politiques pour la jeunesse, il essayera donc de décrédibiliser son adversaire après des jeunes, quitte à se décrédibiliser lui-même.

Le système par approbation

C’est ce qu’il passe lorsqu’un système n’est pas monotone : les stratégies politiques vont être contraintes par le système électoral et poussent les candidats à mal faire leur travail. Pour répondre à ce problème, Balinski a raison de dire que le jugement majoritaire a beaucoup moins de chances que le système à deux tours de produire ce paradoxe, lorsque la population est grande. Néanmoins, il reconnait implicitement que, lorsqu’elle est petite (dans les associations ou groupes militants où ce système est prisé par exemple), il vaut mieux ne pas utiliser le jugement majoritaire.

Le système par approbation, lui, est extrêmement simple. Chacun vote pour autant de candidats qu’il souhaite, et celui qui a plus de voix gagne. Par exemple, si quelqu’un acceptait d’avoir comme président Le Pen et Fillon, mais pas Macron, il voterait pour les deux premiers. D’après les expériences qui ont été menées en France, avec le vote par approbation, il n’y aurait pas eu de changement notable depuis 2002 concernant l’identité du président, sauf en 2007 où le gagnant aurait été probablement Bayrou ⁴¹. Au demeurant, ce résultat permet de ne pas oublier que l’opinion des gens compte aussi. Quand la majorité préfère un candidat aux autres, ce candidat aura plus de chances de gagner, quel que soit le mode de scrutin.

Outre sa simplicité, le vote par approbation a beaucoup de qualités, en particulier celle d’être monotone. Autrement dit, il est impossible, avec ce système, que les paradoxes décrits plus haut apparaissent. Ainsi, tous les candidats ont intérêt à satisfaire un maximum d’électeurs.

Une affaire de marketing ? Le succès du jugement majoritaire

J’avoue que, à ce jour, je continue de penser que le système par approbation est meilleur que le jugement majoritaire. Mais j’ai été impressionné par la campagne dont ce dernier a bénéficié en France. Un système électoral, au fond, est comme une marque de vêtement. Sa qualité n’est pas suffisante pour être vendu, il faut également de la publicité.

Lorsqu’on se rend sur wikipedia.fr, l’article sur le jugement majoritaire compte presque 3000 mots, alors que celui sur le vote par approbation n’en a que 576. On pourrait avoir l’impression que ce dernier est la petite lubie de quelques snobs. Mais en regardant de plus près, l’article sur le vote par approbation existe en 21 langues, alors que l’article sur le jugement majoritaire en 4 seulement. En anglais, il faut 2500 mots pour expliquer le jugement majoritaire, 6300 pour expliquer le vote par approbation. La qualité de ce dernier peut aussi s’apprécier par le fait que l’association états-unienne de mathématique (qui inclue les spécialistes des théorèmes sur les modes de scrutin) l’a choisi comme mode de scrutin.

Evidemment, le fait que le jugement majoritaire ait été créé par des chercheurs français, qui en ont fait une grande publicité en France, ne le discrédite pas. Mais il ne devrait pas l’avantager pas non plus. Or, cette publicité produit une exposition sélective : beaucoup de personnes finissent par connaitre le jugement majoritaire, mais sans connaitre ses alternatives, comme le vote par approbation. Sans trop y réfléchir, donc, le français boira du vin et soutiendra le jugement majoritaire. L’américain, lui, optera pour le soda et le vote par approbation. Mais c’est seulement en y réfléchissant qu’on peut se faire un véritable avis. Personnellement, après avoir pesé le pour et le contre, je prends le vin et le vote par approbation.

CorteX_Chiffres_de_la_delinquance_Diagrammes_Surrepresentation

Sciences politiques et Statistiques – Analyse de chiffres sur la délinquance

19 septembre 201920 mai 2020 Le CorteX

Dans les nombreux débats sur la délinquance ⁴² pleuvent chiffres et statistiques, la plupart du temps sans qu’aucune précaution ne soit prise pour replacer ces chiffres dans leur contexte ou pour expliquer ce qu’ils traduisent réellement.
Pourtant, ces chiffres, particulièrement difficiles à obtenir que ce soit pour des raisons techniques ou éthiques, ont un impact très fort sur les représentations que nous nous faisons de la situation. Il m’a donc semblé important de faire un bilan de ce qui était vérifié et ce qui ne l’était pas, pour lutter contre les idées reçues et leurs conséquences sociales.

Le matériau de base de cet article est le fameux débat entre B. Murat et E. Zemmour chez T. Ardisson.
Une des notions statistiques clés abordées ici est la notion de surreprésentation.

Extrait de Salut les terriens, 6 Mars 2010.

Retranscription de la fin de la discussion :
B. Murat : Quand on est contrôlé 17 fois dans la journée, ça modifie le caractère
E. Zemmour : Mais pourquoi on est contrôlé 17 fois par jour ? Pourquoi ? Parce que la plupart des trafiquants sont noirs et arabes. C’est comme ça, c’est un fait !
B. Murat : Pas forcément, pas forcément.
E. Zemmour : Ben, si.

A la suite de cette émission, E. Zemmour déclare dans Le Parisien du 08.03.2010 :

Ce n’est pas un dérapage, c’est une vérité. Je ne dis pas que tous les Noirs et les Arabes sont des délinquants ! Je dis juste qu’ils sont contrôlés plus souvent parce qu’il y a plus de délinquance parmi eux. Demandez à n’importe quel policier.

Avant-propos

Si le but premier de ce travail est d’analyser ces échanges d’un point de vue statistique, il me semble tout de même nécessaire de commencer par faire quelques remarques :

Autorité
Quelle est la l’expertise de E. Zemmour et B. Murat sur le sujet ? Ont-ils une expertise scientifique c’est-à-dire dépassant le cadre de la simple opinion ? Ont-ils réalisé une étude sociologique sur la question ? Ont-ils réalisé un bilan des connaissances sur le sujet ? Si la réponse est non, il y a de fortes chances qu’ils n’expriment sur ce plateau qu’une opinion personnelle. Se poser cette question (et aller chercher la réponse) est essentiel pour déceler d’éventuels arguments d’autorité.
Source de l’information – Le témoignage
Quelles sont les sources des deux protagonistes ?
Pour B. Murat, on ne sait pas.
Pour E. Zemmour, n’importe quel policier. Mais n’oublions pas ce proverbe critique (ou facette zététique) : un témoignage, mille témoignages, ne font pas une preuve. Le fait que mille personnes assurent avoir vu des soucoupes d’extra-terrestres n’est pas une preuve de leur existence.
Prédiction auto-réalisatrice
Les propos d’E. Zemmour constituent une prédiction auto-réalisatrice. Considérons en effet qu’un délinquant est quelqu’un qui a été qualifié comme tel après avoir été arrêté par la police et acceptons momentanément les prémisses d’E. Zemmour :
(a) La plupart des trafiquants sont Noirs et les Arabes
(b) Le contrôle d’identité est efficace pour détecter des trafiquants.
Si une majorité de policiers pensent que la phrase (a) est vraie, ils tendront à contrôler plus les Noirs et les Arabes. Et si la phrase (b) est vraie, ils tendront à trouver, de fait, plus de délinquants Noirs et Arabes. Ils conforteront ainsi les dires d’E. Zemmour.
Plurium interrogationum, essentialisation et effet cigogne
Dans la dernière partie de ce travail, nous discutons du sens et de la validité statistique de la phrase Il y a plus de délinquance chez les Noirs et les Arabes, mais nous n’aborderons pas une autre prémisse qui, même si ce n’est pas l’intention de l’auteur, est très souvent entendue dans cette même phrase : Les Noirs et les Arabes sont plus délinquants (par essence) que les Autres.
L’analyse de cette prémisse, ou plus exactement du raisonnement Il y a plus de Noirs et d’Arabes en prison ; on peut en déduire que les Noirs et les Arabes sont plus délinquants que les Autres fera l’objet d’un TP à part entière. C’est un bel exemple d’effet cigogne.
En attendant, vous pouvez lire un article sur ce sujet dans le livre Déchiffrer le monde de Nico Hirtt, intitulé Méfiez-vous des grandes pointures ; il y est expliqué comment d’autres variables sont corrélées, tout autant que la variable « être Noir ou Arabe », à la fréquentation des prisons : pauvreté économique mais aussi niveau scolaire faible, avoir des parents analphabètes ou… avoir de grands pieds – nous laissons soin au lecteur de trouver une raison à cette dernière observation. Ce dernier exemple permet, il me semble, de mesurer à quel point une corrélation interprétée sans précaution comme une causalité peut se révéler être un non sens total.

Première partie : que représentent les chiffres de la délinquance ?

B. Murat comme E. Zemmour s’appuient sur des chiffres pour étayer leurs propos et placent ainsi le débat dans le domaine des statistiques. Ils ont tous les deux beaucoup d’assurance et s’expriment comme si les chiffres allaient de soi et étaient connus de tous.
Or, quand des chiffres sont avancés pour étayer un argumentaire sur la délinquance, il est parfois très difficile de comprendre de quoi l’on parle exactement, ce que l’on aurait voulu dénombrer et ce que l’on a vraiment compté.
D’ailleurs, les organismes qui produisent ces chiffres précisent et décrivent très minutieusement ce qu’ils ont dénombré exactement ; leurs chiffres sont à prendre pour ce qu’ils sont, et non pour ce qu’on voudrait qu’ils soient.

Voici quelques citations parmi d’autres issues de la description de la méthodologie utilisée par la Direction centrale de la police judiciaire pour réaliser le rapport intitulé Criminalité et délinquance constatées en France (2007).

Que choisit-on de compter pour décrire la criminalité et la délinquance en France ?

Page 12 : B – LA REPRÉSENTATIVITÉ DES STATISTIQUES
Que représentent les statistiques de la criminalité et de la délinquance constatées par les services de police et les unités de gendarmerie ? Autrement dit, quelles en sont les limites dans le champ des infractions ?
1 – LE CHAMP DES STATISTIQUES
Il ne comprend pas les infractions constatées par d’autres services spécialisés (Finances, Travail…), les contraventions, les délits liés à la circulation routière ou à la coordination des transports.
La statistique ne couvre donc pas tout le champ des infractions pénales. Elle est limitée aux crimes et délits tels que l’opinion publique les considère. Elle correspond bien à ce que l’on estime relever de la mission de police judiciaire (police et gendarmerie).

Tri sélectif de données : on peut constater un premier tri sélectif des données : ne sont comptés que les crimes et délits constatés. On sait cependant que dans certains cas, les victimes n’osent pas parler, comme par exemple les victimes de viols, les hommes et les femmes battus ou le harcèlement au travail…

Opinion publique pour légitimer un second tri sélectif : on peut également se demander qui est l’opinion publique et le on qui définissent si clairement ce qu’est ou non une infraction pénale. Et quelles sont les bases qui permettent à l’auteur du rapport d’affirmer que l’opinion publique ne considère pas comme infraction relevant du pénal des infractions au droit du travail, ou les circuits financiers clandestins, le blanchiment d’argent, voire le financement du terrorisme ⁴³, qui relèvent du service TRACFIN du ministère des finances. Un deuxième tri sélectif des données est opéré.

Plus précisément, comment sont créées les variables statistiques (ici, les désignations de tel ou tel délit) ?

Page 13 : 2 – LE RAPPORT DES STATISTIQUES À LA RÉALITÉ
Il n’y a pas de criminalité « en soi » mais des comportements désignés comme illicites par la collectivité. Tout naturellement, ces comportements sont alors dénombrés à partir des « désignations » que constituent les procédures judiciaires. Un comportement illicite non « désigné » aux autorités judiciaires n’est donc pas pris en compte.

– «comportements désignés» : par qui ?
– Comme illicites : donc en vertu d’une loi, qui peut changer ; par exemple, l’adultère n’est plus puni pénalement depuis 1975
– par la collectivité : qui est la collectivité ? Comment s’exprime-t-elle ?

Au regard des trois derniers points, le Tout naturellement semble pour le moins incongru ; d’autant plus quand, dans la phrase précédente, il est explicitement dit Il n’y a pas de criminalité « en soi ». Il semble donc, au contraire, que la désignation des délits relève d’un choix : il est décidé que l’on comptera un acte comme délit s’il peut être désigné par une des procédures judiciaires répertoriées au préalable, cette liste étant décidée par la collectivité. Et ce choix peut évoluer. Rien de naturel donc.

Comment interpréter la variation d’une variable ?

Page 13 : Par ailleurs, il faut noter que le nombre de faits constatés peut s’accroître ou diminuer selon l’importance des moyens mis en oeuvre pour combattre un phénomène (comme par exemple la toxicomanie) ou à la suite de variation dans le mode de sanction des infractions (par exemple, la dépénalisation en 1991 des chèques sans provision d’un faible montant)

Effet cigogne : ce qui se dit ci-dessus permet de prédire une floppée d’effets cigognes dans les médias, lors de repas dominicaux ou sur les terrasses de cafés : la variation d’un chiffre ne reflète pas nécessairement la variation du nombres de délits effectifs mais peut refléter une hausse des moyens mis en oeuvre pour le combattre. C’est un biais très sérieux. Par exemple, plus il y a d’agents sur le terrain pour mesurer la vitesse des automobilistes, plus il y a d’excès de vitesse constatés. Il n’est absolument pas possible d’en conclure qu’il y a de plus en plus de chauffards.
Vous repèrerez quasiment tous les jours des effets cigognes à ce sujet dans vos médias préférés.

Comment sont produites les données ?

Page 13 : 3 – LA QUALIFICATION DES FAITS
[…] Chaque fait à comptabiliser est affecté à tel ou tel index de la nomenclature de base en fonction des incriminations visées dans la procédure. Naturellement, il ne s’agit que d’une qualification provisoire attribuée par les agents et officiers de police judiciaire en fonction des crimes et délits que les faits commis ou tentés figurant dans les procédures sont présumés constituer. Seules les décisions de justice établiront la qualification définitive, quelques mois et parfois plus d’une année après la commission des faits. Or, il ne saurait être question d’attendre les jugements pour apprécier l’état de la criminalité, de la délinquance et de ses évolutions.

Effet paillasson : Une fois les variables créées, il est dit explicitement que, par manque de temps, il n’est pas possible d’attendre une désignation définitive des faits, ce qui rajoute un biais. Comment, en effet, s’assurer que la qualification des faits par un agent de police est celle qui sera retenue par la suite ? D’autant plus que l’agent n’est pas un observateur neutre, la qualification des faits pouvant influencer sa propre évaluation par ses supérieurs ; il est alors envisageable que cela puisse modifier, même de manière involontaire, son évaluation de la situation. Par ailleurs, rien n’assure que la personne poursuivie pour ce crime ou ce délit sera jugée coupable.

Conclusion

Tris sélectifs et invocation de l’opinion publique voire pour définir ce qui constitue un acte de délinquance, non indépendance des variables « nombre de délinquants » et « nombre d’agents luttant contre la délinquance », relevé des données biaisé : ces chiffres sont à utiliser avec de nombreuses précautions.

2ème partie : quelles statistiques sur le contrôle d’identité

Propos de B. Murat :

« Quand on est contrôlé 17 fois par jour »

Quelles sources disponibles ? Quelle méthodologie ? Quels résultats ?
Quelles conséquences d’une mauvaise utilisation des chiffres ?

D’où vient le chiffre 17 ?

Comme B. Murat ne cite pas ses sources, on peut émettre différentes hypothèses : il connaît quelqu’un qui connaît quelqu’un (Ami d’un ami) et l’information mériterait d’être vérifiée ; ou il utilise une exagération pour mettre en relief son propos (effet impact d’une hyperbole) ; ou il a lu une étude sur le sujet ; ou il propage une idée commune mais non vérifiée. Je n’ai trouvé trace d’aucune étude énonçant ces chiffres, mais il existe une étude sur le sujet, menée en 2009 par deux membres du CESDIP – laboratoire de recherche du CNRS mais également service d’études du ministère de la Justice – F. Jobard et R. Lévy , intitulée Police et minorité visible : les contrôles d’identité à Paris.
Je n’en ai pas trouvé d’autres. Il est d’ailleurs dit p. 9 du rapport : Cette étude, qui présente des données uniques sur plus de 500 contrôles de police, est la seule menée à ce jour, propre à détecter le contrôle à faciès en France.

Quelle méthodologie et quelles notions pour établir des satistiques sur les contrôle au faciès ?

F. Jobard explique la méthodologie employée :

{avi}CorteX_Delinquance1_Jobard_Methodologie_controle_identite{/avi}

Les notions de surreprésentation et d’odds-ratio :
Que signifie la phrase « Telle catégorie est plus contrôlée que telle autre » ? Comment le mesurer ?
Quand on parle de surreprésentation, il faut faire attention à ne pas détacher des données importantes ; par exemple, si 10 Noirs et 5 Blancs ont été contrôlés, on ne peut pas affirmer pour autant que les Noirs sont 2 fois plus contrôlés que les Blancs. En effet, si les contrôles se font dans un lieu où se trouvent deux fois plus de Noirs que de Blancs, la population Noire contrôlée n’est pas surrepésentée dans la population contrôlée.

Dans la première population imaginée, nous avons :
– 1 000 Noirs ou Arabes (bleu)
– 500 Blancs (orange)
– 10 trafiquants Noirs ou Arabes (bleu)
– 2 trafiquants Blancs (orange)

Les Noirs et les Arabes sont surreprésentés.

Dans la deuxième population imaginée, nous avons :
– 1 000 Noirs ou Arabes (bleu)
– 500 Blancs (orange)
– 10 trafiquants Noirs ou Arabes (bleu)
– 5 trafiquants Blancs (orange)

Les Noirs et les Arabes ne sont pas surreprésentés.

Il faut donc impérativement connaître la composition de la population globale du lieu d’observation avant de conclure à la surreprésentation et utiliser un outil statistique qui en rende compte, par exemple le odds-ratio dont vous pourrez trouver une définition sur wikipedia.

F. Jobard et R. Lévy nous expliquent comment l’interpréter :

L’odds-ratio compare entre elles les probabilités respectives de contrôle des différents groupes Les odds-ratios présentés dans ce rapport ont tous comparé les groupes relevant des minorités visibles à la population blanche, de sorte que l’odds-ratio se lit de la manière suivante : « Si vous êtes Noir (ou Arabe, etc.), vous avez proportionnellement x fois plus de probabilités d’être contrôlé par la police que si vous étiez Blanc ». L’odds-ratio est reconnu comme la meilleure représentation statistique de la probabilité affectant différents groupes d’une même population compte tenu de la composition de cette population.
L’absence de contrôle au faciès correspond à un odds-ratio de 1,0 : les non-Blancs n’ont pas plus de probabilité d’être contrôlés que les Blancs. Les odds-ratios allant de 1,0 à 1,5 sont considérés comme bénins, ceux allant de 1,5 à 2,0 comme le signe d’un traitement différencié probable. Les ratios supérieurs à 2,0 indiquent qu’il existe un ciblage des minorités par les contrôles de police.

Quels sont les résultats de l’étude ?

Sur l’ensemble des 5 lieux d’observation, les Noirs (resp. les Arabes) ont entre 3,3 et 11,5 fois (resp. entre 1,8 et 14,8) plus de chances d’être contrôlés que les blancs. Le contrôle « au faciès » est donc avéré.
Cependant, d’autres variables sont importantes, en particulier la tenue vestimentaire. Comme il l’est précisé dans le résumé de l’étude p. 10.
Il ressort de notre étude que l’apparence vestimentaire des jeunes est aussi prédictive du contrôle d’identité que l’apparence raciale. L’étude montre une forte relation entre le fait d’être contrôlé par la police, l’origine apparente de la personne contrôlée et le style de vêtements portés : deux tiers des individus habillés « jeunes » relèvent de minorités visibles. Aussi, il est probable que les policiers considèrent le fait d’appartenir à une minorité visible et de porter des vêtements typiquement jeunes comme étroitement liés à une propension à commettre des infractions ou des crimes, appelant ainsi un contrôle d’identité.
Il est important de noter que plusieurs corrélations – entre « être Noir ou Arabe », « être habillé jeune » et « être contrôlé »- sont établies. La relation de causalité « être Noir ou Arabe » implique « être contrôlé » mérite donc d’être discutée. En effet, si nous exagérons les faits et que nous supposons que tous les Noirs et Arabes et seuls les Noirs et les Arabes s’habillent jeunes, on ne saurait pas si le critère du contrôle est « être Noir ou Arabe » ou « être habillé jeune ».
En réalité, la force prédictive de ces deux variables est à peu près équivalente.[…]En tout état de cause, même si l’apparence vestimentaire était la variable-clé de la décision policière, cela aurait un impact énorme sur les minorités visibles, dans la mesure où leurs membres sont plus susceptibles que les Blancs d’arborer une tenue « jeune ». En effet, deux tiers des personnes en tenue « jeune » appartiennent également à une minorité non-Blanche. Si l’on considère les trois groupes principaux, seulement 5,7% des Blancs de la population de référence portent une tenue « jeune », contre 19% des Noirs et 12,8% des Arabes. En d’autres termes, on peut dire de la variable « tenue jeune » qu’elle est une variable racialisée : lorsque la police cible ce type de tenues, il en résulte une surreprésentation des minorités visibles, en particulier des Noirs, parmi les contrôlés.
Sur la fréquence des contrôles (attention, ces chiffres sont basés sur la déclaration des personnes contrôlées et n’ont pas été établis de manière rigoureuse).
À la question de savoir si c’était la première fois qu’elles étaient contrôlées, une grande majorité de personnes interrogées (82%) a répondu par la négative. 38% ont indiqué être contrôlées souvent, 25% ont indiqué avoir été contrôlées de deux à quatre fois par mois, et 16% ont indiqué être contrôlées plus de cinq fois par mois. Il faut remarquer que l’éventail du nombre de contrôles dans cette dernière catégorie était étendu, les personnes indiquant avoir été contrôlées entre cinq et neuf fois le mois précédent, jusqu’à un total de 20 fois.

Quelles conséquences des approximations contenues dans les propos de B. Murat ?

Il est probable que B. Murat ait gonflé ce chiffre pour appuyer son discours, et qu’il ne pensait pas vraiment que le fait de contrôler les mêmes personnes 17 fois par jour est une pratique courante dans les banlieues.

Cependant, n’oublions pas que B. Murat pour répond à l’argument : « Il y a de la délinquance dans les banlieues ». On peut alors penser qu’il sous-entend qu’une des causes de cette délinquance est la répétition des contrôles. Si cela semble plausible pour, par exemple, ce qui concerne le délit d’outrage à agents – plus on est contrôlé, plus le nombre d’occasions « d’outrager » un agent de police est élevé – je ne connais pas d’étude qui démontrerait cette relation de cause-conséquence dans le cadre général. Ceci est probablement un effet cigogne.

En revanche, ce que tend à montrer la partie qualitative du rapport de F. Jobard et R. Lévy, c’est que le contrôle d’identité est perçu comme une agression par les personnes qui en sont les cibles, même si la plupart du temps et selon l’avis même des personnes contrôlées, le contrôle est mené sans agressivité de la part des agents.

Malgré le caractère généralement neutre ou positif des jugements sur le comportement de la police, ces contrôles ont suscité des sentiments très négatifs. Quelques personnes ont simplement déclaré que la police ne faisait que son travail et que le contrôle ne les avait pas dérangées. Mais près de la moitié des personnes interrogées ont indiqué être agacées ou en colère du fait du contrôle.[…] Le préjudice que les pratiques de contrôle de police causent à la relation que la police entretient avec les personnes objet de contrôle est manifeste.

Cette pratique est ressentie comme violente et humiliante par ceux qui la vivent donc la question de son efficacité mérite d’être posée. Je précise ma pensée : si le but de la politique est de minimiser la souffrance globale de la population et si le contrôle est vécu comme violent, il me semble tout de même nécessaire de s’assurer du fait que cette pratique est indispensable pour lutter contre une autre violence, celle dite « de la délinquance ». Savoir si cette condition est suffisante pour légitimer le contrôle d’identité est encore une autre question.

Partie 3 : quelles statistiques ethniques de la délinquance ?

Propos d’E. Zemmour :

« La plupart des trafiquants sont noirs et arabes. »

Quelles variables aléatoires ? Quelles sources ? Quelles conclusions ?

Trame du raisonnement :
a. La plupart des trafiquants sont noirs et arabes
+ b. Le contrôle d’identité permet d’attraper les trafiquants
=> c. En contrôlant plus les noirs et les arabes, on attrapera plus de trafiquants,

Pour tester la validité de la prémisse a, notons que la phrase La plupart des trafiquants sont Noirs et Arabes est une affirmation statistique, mal énoncée certes, mais relevant de la statistique tout de même. E Zemmour sous-entend donc que ces satistiques existent et que quelqu’un a dénombré tous les trafiquants (T), puis les trafiquants Arabes (Ta) ou Noirs (Tn) et a calculé le rapport (Ta+Tn)/T et a trouvé ainsi une probabilité supérieure à 0,5.

Quelles variables statistiques dans la prémisse (a) ?

Le « nombre de trafiquants » est une mauvaise variable statistique. On ne sait même pas de quel trafic on parle : de voitures, de drogue, de subprimes, d’armes, de sous-marins, de cigarettes, d’organes, de diamants, d’oeuvres d’art… ?
On peut supposer qu’E. Zemmour pense au trafic de drogue. Soit. Mais de quelle drogue ?
Comment peut-on compter les trafiquants ? Ceux qu’on a attrapés ? Ceux qui détenaient beaucoup de drogue ? Un peu ? Sont-ils représentatifs de la population des trafiquants ? Considère-t-on qu’on est trafiquant dès lors qu’on a « trafiqué » une fois ?
Une variable statistique pertinente – dans le sens : que l’on peut dénombrer convenablement – serait, par exemple, le « nombre de personnes condamnées pour détention de cannabis ». Une phrase qui aurait un sens statistique serait : « Il y a plus de Noirs et d’Arabes parmi les personnes condamnées au moins une fois dans les 5 dernières années pour une infraction sur les drogues ». Cette phrase a un sens; elle peut être vraie ou fausse.

« Etre Noir » ou « être Arabe » ou « être Blanc » sont également de mauvaises variables statistiques. Quand commence-t-on ou arrête-t-on d’être Noir, Arabe ou Blanc ? Quand un des parents l’est ? Ou bien les deux ? Ou une grand-mère suffirait ? Pour « trancher » la question, certains pensent même à utiliser la consonance du nom de famille, comme cela a déjà été fait dans un article du Point :

Le Point a pu consulter ces notes, dans lesquelles il apparaît que plus de la moitié, voire 60 ou 70%, des suspects répertoriés ont des noms à consonance étrangère. Cet élément est délicat à manipuler. En aucun cas l’on ne saurait déduire avec certitude une origine d’un patronyme. Il ne s’agit pas non plus de tirer des conclusions absurdes sur un caractère « culturel » de la criminalité. Mais écarter ces constatations d’un revers de manche est une grave erreur qui occulte l’échec de l’intégration.

On remarquera que la gravité de la conclusion, occulter l’échec de l’intégration, méritait pourtant qu’on s’assure de la qualité des prémisses du raisonnement.

Quelles sources pour les statistiques ethniques ou raciales dans la prémisse (a) ?

Si le fait d’établir des statistiques ethniques est en général illégal, certaines dérogations sont accordées par la CNIL. Par exemple, elle peut autoriser sous certaines conditions la collecte d’informations sur le pays d’origine des individus ou de leurs parents (on pourra aller consulter les 10 recommandations de la CNIL ). Comme le rapporte un article du Monde du 05/02/2010 :

De fait, si la loi Informatique et liberté de 1978 énonce une interdiction de principe sur le traitement statistique des données sensibles, elle permet d’y déroger, sous contrôle de la Commission nationale informatique et libertés (CNIL) et à condition de respecter certains critères (consentement individuel, anonymat, intérêt général…).

Notons toutefois qu’il n’existe pas de statistiques sur des « variables » du type Blancs, Arabes et Noirs, à une exception près, exception de taille : à mon grand étonnement je l’avoue, il existe un fichier confidentiel, nommé Fichier Canonge, qui classe les « délinquants » par « type » physique. Voici ce qu’en dit l’Express du 07/02/2006 :

A quoi ressemblent les délinquants de tous les jours? Pour le savoir, il suffit de se plonger dans un fichier méconnu, baptisé «Canonge», qui comporte l’état civil, la photo et la description physique très détaillée des personnes «signalisées» lors de leur placement en garde à vue. Grâce à cette base de données présentée à la victime, celle-ci peut espérer identifier son agresseur. Or ce logiciel, réactualisé en 2003, retient aujourd’hui 12 «types» ethniques: blanc-caucasien, méditerranéen, gitan, moyen-oriental, nord-africain-maghrébin, asiatique-eurasien, amérindien, indien, métis-mulâtre, noir, polynésien, mélanésien.

Cet outil est à manier avec prudence. D’abord, parce que, même si le Canonge est légal, la Commission nationale de l’informatique et des libertés (Cnil) interdit d’exploiter ses renseignements à d’autres fins que celle de la recherche d’un auteur présumé. Ensuite, parce qu’il ne dit rien de la nationalité et de l’origine de l’individu – qui peut être français depuis plusieurs générations malgré un physique méditerranéen, par exemple. Enfin, parce que les mentions sont portées par l’officier de police, avec la part de subjectivité que cela suppose.

Remarque : les mêmes précautions sont à prendre qu’avec les chiffres du rapport Criminalité et délinquance constatées en France (tris sélectifs de données, prédicion auto-réalisatrice, subjectivité des observateurs…)

Quelle population de référence pour établir la surreprésentation dans la prémisse (a) ?

Quand E. Zemmour prétend que la plupart des trafiquants sont Noirs ou Arabes, il énonce un résultat de surreprésentation : les Noirs ou les Arabes sont surreprésentés dans la population des trafiquants. Mais cela ne vous a pas échappé : cette notion n’a de sens que si l’on connaît la population de référence. Il est probable qu’E. Zemmour considère la population résidant en France, mais cela n’a pas vraiment de sens, puisque toutes ces personnes ne vivent pas forcément dans des conditions externes égales. Pour savoir si les Noirs ou les Arabes sont surreprésentés, il me semblerait préférable de considérer la population « susceptible d’être délinquante » (si tant est qu’on puisse donner un sens rigoureux à cette expression), c’est-à-dire celle qui vit dans les mêmes conditions que les « délinquants ».

Quelle probabilité conditionnelle dans l’implication (a)+(b) => c ?

Les prémisses (a) et (b) n’entraînent pas (c). Nous avons là un bel exemple de sophisme Non sequitur, dû à une erreur d’inversion de probabilité conditionnelle.
On retrouve le même sophisme dans les phrases suivantes, où il est plus facile à repérer

La plupart des pédophiles sont Blancs donc il faut plus contrôler les Blancs.
OU
La plupart des inculpés français dans l’affaire des frégates de Taïwan sont Blancs donc il faut plus contrôler les Blancs.
OU
Tous les incestes sont commis par un membre de la famille donc il faut contrôler tous les membres de sa famille

En fait, E. Zemmour s’emmèle les probabilités conditionnelles.

Ce n’est pas parce que la proportion de Noirs et d’Arabes est importante dans la population des trafiquants – dans ce cas on considère P(N U A/T) – que la proportion de trafiquants est importante dans la population Noire et Arabe – ici on regarde P(T/N U A). Vous en serez encore plus convaincu si vous prenez les autres versions du sophisme.

Exemple :
Imaginons une population composée de 1 000 personnes, dont :
– 400 Noirs ou Arabes
– 600 Blancs
– 7 trafiquants : 5 Noirs ou Arabes et 2 Blancs
Dans cet exemple,
P(NUA / T) = Nombre de Trafiquants Noirs ou Arabes / Nombre de Trafiquants ≈ 71,4%
P(T / NUA) = Nombre de Trafiquants Noirs ou Arabes / Nombre de Noirs ou Arabes ≈ 1,2%
Les ordres de grandeur sont radicalement différents.

Notons qu’E. Zemmour revient sur ce point dans le Parisien et le rectifie. Cependant, quand il dit « Je dis juste qu’ils sont contrôlés plus souvent parce qu’il y a plus de délinquance parmi eux« , le parce que légitime la pratique du contrôle et sous-entend qu’on a des chances d’attraper des trafiquants de cette manière et donc que la probabilité P(T/A U N) est élevée ; sa prémisse de départ est, rappelons-le, que P(A U N/T) est élevée.

Quelles conséquences des approximations contenues dans les propos d’E. Zemmour ?

Ces propos sont très essentialistes même, encore une fois, si ce n’était pas l’intention de l’auteur. La phrase « La plupart des trafiquants sont Noirs ou Arabes » est très souvent entendue comme « Ils sont délinquants parce qu’ils sont Noirs ou Arabes » (effet cigogne), ce qui n’a aucun fondement scientifique et qui exacerbe le racisme.

Mais au fait, quelle est la probabilité d’attraper un trafiquant lors d’une journée de contrôles d’identité ?

Cette partie est conçue pour pousser votre public à se méfier des statistiques, y compris quand c’est vous qui les présentez. Je vous propose pour cela de faire de mauvaises statistiques sans en avoir l’air. Si un membre du public réagit, vous avez gagné la partie. S’il n’y a pas de réactions spontanées, cela vous donnera l’occasion de pointer du doigt
1. la nécessité d’être vigilant en permanence : même averti, on n’est pas à l’abri d’une entourloupe, volontaire ou non,
2. qu’il ne faut pas croire sur parole la personne qui essaie de vous transmettre des outils critiques.

Attention : Mauvaises statistiques ! Les chiffres obtenus dans ce qui suit ne représentent absolument rien.
– Dans l’article de l’Express sur le fichier Canonge, il est dit que sur 103 000 trafiquants fichés, il y a 29% de Nord-Africains et 19% de Noirs.
En tout, cela fait 49 440 trafiquants Noirs ou Arabes.

– On peut évaluer à environ 2 988 745 personnes Noires ou Arabes en France.

– La probabilité de tomber sur un délinquant en contrôlant un Noir ou un Arabe au hasard est donc à peu près de 49 440 / 2 988 745 ≈ 1,7%.

– F. Jobard et R. Lévy rapportent p. 62 que le nombre moyen de contrôles observés par heure est de 1,25. Ce qui fait 8,75 contrôles pour 7 heures travaillées. Disons 9 contrôles par jour.

– En remarquant que la variable aléatoire « nombre de trafiquants attrapés dans la journée » suit une loi binomiale, on obtient la conclusion suivante :
la probabilité d’attraper au moins un trafiquant dans la journée en contrôlant les Noirs et les Arabes est d’environ 14,2%. Sur 100 journées de contrôles d’identité, une équipe qui pratique les contrôles d’identité revient sans trafiquant 85 fois.

Vous venez de créer une occasion pour votre public d’analyser vos propos de manière critique :
Vous êtes-vous posé la question de savoir d’où sortait le chiffre du nombre de Noirs et Arabes en France ? Ce n’est en fait qu’une estimation, très mauvaise, faite avec les moyens du bord et très critiquable.
Je suis allée sur le site de l’INSEE où figurent des données – cliquer sur Données complémentaires, sur cette page et consulter le graphique 2 – sur le nombre de personnes entre 15 et 50 ans dont au moins un des parents est immigré de Turquie, d’Afrique Subsaharienne, du Maroc, de Tunisie ou d’Algérie : il y en a 1 282 000.
Par ailleurs, sur le site de l’INED, on peut télécharger le document Immigrés selon le sexe, l’âge et le pays de naissance 2007. Dans l’onglet France détail, on peut lire qu’il y a en France en 2007, 1 706 745 immigrés issus du continent Africain et qui ont entre 18 ans et 59 ans.

Ensuite, j’ai appliqué une grande dose de racisme ordinaire : ceux qui viennent (ou dont un parent vient) d’Europe sont blancs, ceux qui viennent du Maghreb sont Arabes et ceux qui viennent d’Afrique Noire sont Noirs. Les Antillais qui sont Français sont comptés comme Blancs, les Français dont les deux parents sont Français sont comptés comme Blancs etc…

Remarquez que, sur wikipedia (version du 19/01/2011), on peut lire

En 2010, la France accueille 6,7 millions d’immigrés (nés étrangers hors du territoire) soit 11% de la population. Elle se classe au sixième rang mondial, derrière les Etats-Unis (42,8 millions), la Russie (12,3), l’Allemagne (9,1), l’Arabie Saoudite (7,3), le Canada (7,2) mais elle devance en revanche le Royaume-uni (6,5) et l’Espagne (6,4). Les enfants d’immigrés, descendants directs d’un ou de deux immigrés, représentaient, en 2008, 6,5 millions de personnes, soit 11 % de la population également. Trois millions d’entre eux avaient leurs deux parents immigrés. Les immigrés sont principalement originaires de l’Union européenne (34 %), du Maghreb (30 %), d’Asie (14 %, dont le tiers de la Turquie) et d’Afrique subsaharienne (11 %).

En reprenant les calculs avec ces chiffres – à savoir 41% de 6,7 millions + 6,5 millions-, on obtient une probabilité d’attraper au moins un trafiquant en une journée de 8% environ. Encore faudrait-il savoir à quoi correspondent ces données exactement ? Les sources de l’article de wikipedia sont :

Les immigrés constituent 11% de la population française [archive], TF1, Alexandra Guillet, le 24 novembre 2010, source : Ined

Etre né en France d’un parent immigré [archive], Insee Première, N° 1287, mars 2010, Catherine Borel et Bertrand Lhommeau, Insee

Bref, le calcul est biaisé et il m’est impossible d’évaluer la marge d’erreur commise. Ce chiffre n’a aucune légitimité et ne pourra être brandi d’aucune manière sur un quelconque plateau télé ou lors d’un quelconque dîner de famille.
Mais il permet d’énoncer une conclusion : les chiffres ne parlent pas d’eux-mêmes. Il est important de savoir comment ils ont été élaboré.

Cours Esprit critique et mathématiques au lycée : échantillonnage et zététique

29 mars 201920 mai 2020 Denis Caroti

Louis Paternault est enseignant de mathématiques au lycée Ella Fitzgerald de Saint Romain en Gal (69). Il nous présente une nouvelle séquence (voir la première ici) effectuée avec ses élèves de seconde concernant la notion d’échantillonnage et pour laquelle il utilise une expérience fictive d’un sourcier cherchant à prouver son « pouvoir ». Il aborde également les notions de charge de la preuve et d’échelle des preuves. L’article rédigé par Louis est déjà publié et mis en forme sur son blog, nous le reproduisons ici avec son autorisation. Merci et bravo encore à lui !

Téléchargements

Voici les fichiers utilisés pour cette séance :

diaporama (source et image) ;
fiche élève (source).

Objectifs

Mathématiques

Cette séance introduit la partie du programme de seconde générale (jusqu’en 2018-2019) qui concerne l’échantillonnage, par exemple : « Exploiter et faire une analyse critique d’un résultat d’échantillonnage. »

En revanche, si l’échantillonnage est toujours dans le nouveau programme, la notion d’intervalle de fluctuation semble avoir disparu, donc cette séance devra être adaptée à partir de l’année scolaire 2019-2020.

Zététique

Cette séance vise à montrer comment l’échantillonnage permet de porter un regard critique sur la société qui nous entoure, et en particulier sur les pseudo-sciences. Elle introduit les maximes « Des affirmations extraordinaires réclament des preuves plus qu’ordinaires » et « La charge de la preuve est à celui ou celle qui affirme. »

Cet objectif s’inscrit également dans le cadre du programme officiel (jusqu’à la réforme du bac 2021), en participant à « donner à chaque élève la culture mathématique indispensable pour sa vie de citoyen ».
Cet activité permet également de poursuivre le développement de la compétence du socle commun : « L’appréhension rationnelle des choses développe les attitudes suivantes : […] l’esprit critique : distinction entre le prouvé, le probable ou l’incertain, la prédiction et la prévision, situation d’un résultat ou d’une information dans son contexte […]. »

Contexte

Mathématiques

Cette séance a eu lieu fin décembre, à la fin du chapitre sur les statistiques. Les élèves avaient donc vu (avec moi la semaine précédente, ou au collège) des notions de statistiques descriptives (moyenne, médiane, quartiles, représentations graphiques). L’échantillonnage, en revanche, était nouveau pour eux.

Ils n’avaient quasiment pas utilisé de calculatrice scientifique.

Zététique

Je n’avais jamais abordé ce type de sujet, et ils n’avaient (à ma connaissance) jamais fait ou entendu parler de zététique.

Déroulement

Cette activité s’est déroulée en une heure et demi (sur deux séances). Le diaporama est utilisé comme support de la majeure partie de la séance.

La première heure a été faite en demi-groupes, et la seconde en classe entière. Il doit être tout à fait possible de faire l’ensemble en classe entière.

Père Noël et Charge de la preuve

La première diapositive du diaporama contient l’affirmation « Le Père Noël existe ». Je demande aux élèves de me prouver le contraire. Extraits de dialogues :

Élève : Ça n’est pas possible de visiter toutes les maisons du monde en une nuit. Il faudrait qu’il dépasse la vitesse de la lumière / son traîneau aurait un poids démesuré / vu la vitesse nécessaire, à cause de la friction de l’air, son traîneau prendrait feu / il ne peut pas livrer des cadeaux dans les maisons sans cheminées…
Prof : Le Père Noël est magique : il n’est donc pas soumis aux lois de la physique.
Élève : Mais la magie n’existe pas !
Prof : Prouvez le moi.

Élève : Ce sont les parents qui apportent les cadeaux.
Prof : Chez vous, peut-être, mais le Père Noël apporte leurs cadeaux aux autres enfants.

Élève : Si le Père Noël existait, il apporterait des cadeaux à tout le monde, or les enfants pauvres n’ont pas de cadeaux.
Prof : Le Père Noël n’aime pas les pauvres.

Élève : Mais la magie n’existe pas. Vous avez déjà vu une licorne ?
Prof : Vous avez déjà vu un rhinocéros ?

Tous les élèves n’ont pas participé à cet échange, mais un bon nombre a essayé d’apporter des preuves. J’ai senti la frustration des élèves, de qui je balayais toutes les tentatives de preuves, ce qui montre leur implication dans l’exercice.

Un élève a finalement remarqué qu’il était nécessaire que je prouve que le Père Noël existe, réflexion que j’ai reprise, et qui m’a permis d’expliquer la maxime « La charge de la preuve est à celui ou celle qui affirme », que j’ai ensuite illustrée avec d’autres exemples (« la nuit dernière, j’ai été enlevé puis relâché par des extra-terrestres ; prouvez-moi que c’est faux » ; « Emmanuel Macron est un lézard à la solde des martiens ; prouvez-moi que c’est faux »). Je n’ai pas mentionné (et les élèves non plus) que le même raisonnement s’applique exactement de la même manière si l’on remplace le Père Noël par Dieu.

Échelle des preuves

Si c’est bien à celui qui affirme de prouver ses propos, nous n’allons pas exiger de nos interlocuteurs qu’ils prouvent chacune de leur affirmation. L’échelle de la preuve¹ arrive alors à point nommé.

Cette échelle n’est pas vraiment utile pour amener la notion de fluctuation d’échantillonnage, mais elle sert à la formation citoyenne : elle explicite la citation d’Henri Poincaré : « Douter de tout ou tout croire sont deux solutions également commodes, qui nous dispensent de réfléchir. »

Sourcier

J’ai ensuite expliqué que nous utilisons la preuve en mathématiques pour démontrer plein de choses, mais jusqu’à maintenant, dans leurs cours de mathématiques, ils ne s’en sont servi, dans la grande majorité, que pour des énoncés mathématiques. Le but de la séance est d’introduire un outil permettant de prouver des énoncés « de la vraie vie ».

J’ai ensuite introduit le cas d’étude suivant : « Une personne affirme être sourcier, c’est-à-dire avoir le pouvoir de détecter des sources d’eau. Comment faire pour confirmer ou infirmer son prétendu don ? ». Peu à peu, l’idée de mettre le sourcier à l’épreuve a émergé, qui devrait être faite en aveugle (je n’ai pas abordé la notion de double aveugle), et enfin, nous avons convenu qu’il fallait répéter cette épreuve, pour limiter l’intervention du hasard (une version plus développée de cette démarche est décrite dans Esprit critique, es-tu là ? par le collectif CorteX).

Nous n’avons pas réalisé l’expérience dans la classe, mais j’ai présenté les résultats (calculés pour être à la limite de l’intervalle de fluctuation à 95 %, tel qu’étudié en seconde) : sur les 50 essais, notre sourcier a eu 30 bonnes réponses. Comment interpréter ce résultat ?

Après d’autres réflexions, nous avons convenu que la question était : une telle réussite peut-elle être attribuée au hasard, ou est-elle la preuve d’un don ? Il nous fallait donc simuler plusieurs expériences, pour voir s’il nous arrivait d’atteindre 30 réussites sur 50 essais.

Simulation

À ce moment-là, j’ai distribué cette fiche (source) aux élèves, qui constituera leur cours pour cette partie du chapitre. Il rappelle le problème (l’expérience du sourcier), et les guide pour la résolution, avant d’introduire la notion d’intervalle de fluctuation.

Chaque table d’élève a utilisé sa calculatrice pour simuler une série de 50 essais, avec une probabilité de réussite de 50 %, et compilé les résultats au tableau. Manque de chance, dans un des deux groupes, nous avons dû conclure, à mon grand regret, qu’autant de succès avaient vraiment peu de chances d’être attribués au hasard, et que le « sourcier » avait sans doute des dons (voir la partie Problèmes).

Intervalle de fluctuation

La dernière phase de l’activité a pris la forme d’un cours magistral plus classique. Après avoir expliqué l’intérêt d’un tel outil (notamment par rapport aux simulations), j’ai présenté l’intervalle de fluctuation [p−1/√n ; p+1/√n] et son utilisation. Après l’avoir appliqué à notre sourcier, nous avons enfin conclu qu’il n’avait pas donné la preuve de ses pouvoirs.

La suite de la fiche présente en exemple le problème suivant : la proportion de femmes à l’Assemblée nationale, inférieure à la moyenne, est-elle le symptôme d’une sous-représentation des femmes à l’Assemblée nationale ?

Problèmes

Lorsque les élèves devaient me prouver que le Père Noël n’existe pas, je réfutais moi-même leurs arguments. Il pourrait être intéressant de leur laisser le temps de les réfuter eux-mêmes.
La simulation a été faite en demi-groupe. Cela pose problème, car l’échantillon n’a alors que 17 individus, ce qui est peu. La conséquence est qu’il est tout à fait possible, avec un échantillon aussi petit, de « prouver » que le sourcier a un don, ce qui est bien dommage…
Les calculatrices TI que j’utilisais dans mon ancien lycée génèrent toutes la même séquence aléatoire. Avec ce modèle, il faut donc initialiser le générateur aléatoire correctement, pour ne pas avoir trente fois la même simulation. Je n’ai pas rencontré ce problème avec les calculatrices Casio.

Cours Esprit critique et mathématiques au lycée : (se) tromper avec les graphiques

1 septembre 201820 mai 2020 Denis Caroti

Louis Paternault est enseignant de mathématiques au lycée Ella Fitzgerald de Saint Romain en Gal (69). Il nous présente ici une séquence effectuée avec ses élèves de seconde et première S concernant l’analyse des graphiques, en étudiant les différents biais qui peuvent se glisser dans leur réalisation et interprétation. Un travail précieux qui utilise des informations réelles, parues dans différents médias, renforçant l’idée que notre esprit critique gagne toujours à être en éveil face aux chiffres et autres présentations numériques dans la vie quotidienne. Merci et bravo à Louis !

L’article rédigé par Louis est déjà publié et mis en forme sur son blog, nous le reproduisons ici avec son autorisation.

Objectif principal

Cette activité de lycée a pour but d’étudier différentes manières permettant de tromper (volontairement ou non) avec des graphiques. En d’autres termes, comment la représentation de vraies données statistiques permet de donner une impression erronée ?

Téléchargement

Pour les personnes pressées, commençons par les documents nécessaires pour réaliser cette séance en classes :

le diaporama ;
les polycopiés pour les deux groupes (groupe A et groupe B) ;
l’énoncé de la séance sur tableur, ainsi que les données de travail ;
l’ensemble des sources à compiler avec $L u a L A T E X$

(fichiers LaTeX et images ; à décompresser avec le logiciel libre 7zip si votre système d’exploitation ne sait pas quoi faire de ce fichier).

Contexte

Cette séquence a été réalisée en accompagnement personnalisé, en seconde et en première S. Je pense qu’elle peut-être réalisée à n’importe quel niveau du lycée général.
Elle a été effectuée en demi-groupes (17 élèves environ).

Objectifs de la séquence

En ce qui concerne le programme de mathématique, cette séquence permet de :

lire, analyser, créer différentes représentations de séries statistiques ;
« faire réfléchir les élèves sur des données réelles et variées » (programme de seconde) ;
manipuler le tableur (principalement pour représenter une série statistique).

Pour l’esprit critique, cette séquence permet :

de voir comment les mêmes données peuvent donner une impression différente selon la manière dont elles sont représentée ;
d’apprendre à ne pas se laisser tromper par de telles erreurs (volontaires ou non).

Déroulement

Cette séquence se déroule en deux parties (d’environ une séance chacune) : dans un premier temps, les élèves étudient des graphiques « réels » (publiés dans des journaux, à la télé, par des partis politiques, etc.) pour établir une liste d’erreurs fréquentes ; dans un second temps, ils sont amenés à créer eux-même un graphique trompeur (qui, à partir de vraies données, donne une impression fausse ou fantaisiste).

Première séance : Analyse de graphiques

Note : J’ai réalisé d’abord cette séance ; ma collègue Céline l’a utilisée et améliorée. C’est sa version que je décris ici.
La professeure commence par présenter oralement l’objectif de la séance :

À partir de données réelles : répertorier différentes manières de tromper les autres en construisant des graphiques (et donc, répertorier aussi des pièges à éviter pour ne pas se tromper en observant des graphiques).

Travail en groupe

Les élèves sont séparés en deux groupes, et doivent prendre un stylo chacun. Chaque groupe se voit distribuer :

les polycopiés groupeA.pdf pour le premier groupe, groupeB.pdf pour le second groupe (dans chacun des deux polycopiés, les mêmes données sont représentées de deux manières différentes, menant à des conclusions différentes) ;
des post-it.

Les élèves ont eu quelques minutes pour analyser chaque graphique et prendre des notes de leurs idées (une par post-it).

Mise en commun

La professeure leur présente la première partie du diaporama (qui reprend les graphiques qu’ils ont eus entre les mains), en leur disant qu’il s’agit des graphiques qu’ils ont analysés sur polycopié, et qu’ils vont répertorier aux tableaux chacune des « manipulations » possibles.
Leurs idées (d’erreurs ou manipulation) sont relevées au cours du diaporama, à partir de leurs post-it, et des nouvelles idées qui peuvent alors venir.
À la fin de cette partie, une liste des erreurs possibles est disponible au tableau (voir ci-dessous).

Nouveaux graphiques

La seconde partie du diaporama est alors projetée, et les élèvent doivent identifier pourquoi les graphiques proposés sont trompeurs, en se référant à la liste construite précédemment.

Seconde séance : Création d’un graphique trompeur

Note : Cette séance n’a pas été réalisée entièrement ; je pense qu’elle prend une ou deux séances d’une heure.
Cette séance se déroule sur tableur, par binôme. Le but de la séance est de créer un graphique trompeur (réalisé à partir de vraies données, mais qui donne une impression fausse ou fantaisiste).

Première partie

Les élèves ont à disposition l’énoncé, et des séries de données statistiques (réelles, mais a priori sans lien entre elles).
Ils doivent tracer différents graphiques (le détail est dans l’énoncé) ; le but est de leur faire manipuler le tableur (différents types de graphiques, plusieurs axes pour un même graphique, axes ne commençant pas à zéro, etc.).

Seconde partie

Après avoir vu comment manipuler des graphiques, c’est au tour des élèves de produire un graphique trompeur : ils doivent produire un graphique qui montre une corrélation entre deux des séries données pourtant sans lien entre elles.
Les données (population, nombre de mariages, dépenses en fruit et légume, entrées au cinéma en France depuis 1960) sont dans un fichier donnees.ods (sur lequel ils ont travaillé dans la partie précédente). Les élèves peuvent sélectionner les données représentées, supprimer celles qui ne servent pas leurs objectifs, mais ils n’ont pas le droit d’inventer ou modifier des données.

Troisième partie

Enfin, il est possible de terminer (je ne l’ai pas fait ; voir la partie Bilan) en faisant présenter aux élèves leurs corrélations bidon de manière aussi convaincante que possible : en les faisant trouver des fausses explications (« la consommation de légumes favorise les mariages car… ») ou des conséquences (« il faut encourager les français à aller au cinéma pour que la consommation de fruits et légumes augmente »).

Bilan

Analyse de graphiques

Les élèves ont semblé apprécier cette séance : ils ont été très dynamiques. Ils ont bien détecté les problèmes et ont fait des commentaires intéressants sur les différents thèmes. L’objectif de la séance (remarquer des erreurs dans les graphiques) semble donc atteint.

Création d’un graphique trompeur

Je n’ai réalisé que partiellement cette séance (j’ai commencé, mais les vacances sont arrivées, et des séances ont été annulées, et finalement, la suite se serait déroulée plus de six semaines après la première partie ; j’ai préféré abandonner) ; ma collègue ne l’a pas réalisée (à cause de la fin de l’année), donc le bilan est très partiel.
La création de graphiques (pas encore trompeurs) a plutôt fonctionné, en demandant leur attention régulièrement pour expliquer comment faire certains gestes techniques (calcul en base 100, deux axes différents, etc.). Comme alternative, je vois :

faire un sujet très dirigé (mais je voulais les laisser tâtonner, pour qu’ils apprennent à chercher) ;
distribuer un mémo sur l’utilisation des graphiques avec LibreOffice.

Seuls quelques binômes se sont essayés à la création de graphiques trompeurs, et seul l’un d’entre eux a été jusqu’au bout, et a réussi à montrer une relation entre deux séries a priori indépendantes. Les autres n’ont pas terminé par manque de temps.
Je pense qu’une séance d’une heure ne suffit pas à faire cette partie : deux séances devraient convenir. La dernière partie (présenter à la classe son graphique) peut servir de variable d’ajustement si les élèves ont terminé trop tôt.

Liste des erreurs

Les erreurs analysées dans cette séquence sont les suivantes :

Utiliser une échelle logarithmique au lieu d’une échelle linéaire (cela peut être parfois très utile, mais c’est trompeur si on ne fait pas bien attention).
Ne pas faire commencer l’axe des ordonnées à 0 (très courant).
Utiliser la 2D ou la 3D pour donner de fausses impressions (doubler l’échelle multiplie les aires par quatre, et les volumes par huit).
Trier les données : effacer celles qui ne nous plaisent pas (particulièrement efficace en sélectionnant la période de temps qui sert notre propos).
Choisir la bonne année de référence pour des indices en base 100 (ce qui est la raison d’être des indices, mais qui peut créer un effet exagéré par rapport à la réalité des données).

Exemples traités

Je donne pour chacun des exemples la question posée aux élèves, sur laquelle porte la manipulation ou l’erreur du graphique.

Évolution des salaires

Qui, des cadres ou des ouvriers, a vu son salaire annuel net moyen augmenter le plus entre 1992 et 2012 ?

Le graphique de droite utilise une échelle logarithmique, alors que celui de gauche utilise une échelle linéaire (à laquelle nous sommes le plus habitués). Ce que montrent ces graphiques, c’est que le salaire des cadres augmente le plus en valeur absolue (graphique de gauche), alors que c’est le salaire des ouvriers qui augmente le plus en taux d’évolution (graphique de droite).
Laquelle des deux réponses est la bonne ? C’est une question politique, pas mathématique.

Évolution du chômage

Le chômage a-t-il :

un peu, ou pas augmenté ?
moyennement augmenté ?
beaucoup augmenté ?

Source : Relevé par Guillemette Reviron, du Cortecs, qui cite elle-même Le Petit Journal (du 29 novembre 2011).

Ces trois graphiques présentent la même information (les mêmes données) de trois manières différentes.

Sur aucun des trois graphiques, l’échelle verticale ne commence à zéro (et sur celui de France 2, elle n’est même pas présente) : cela augmente artificiellement les évolutions.
La légende de l’axe horizontal est difficilement lisible.

Évolution du taux de grévistes

Le nombre de grévistes a-t-il :

peu diminué ?
beaucoup diminué ?

D’après le communiqué de presse de la SNCF du 4 avril 2018 ; relevé par l’émission C’est à vous du 6 avril 2018 (France 5).

L’erreur ici est que l’échelle verticale ne commence pas à 0.
Il est intéressant de rappeler le contexte : ce communiqué a été publié durant une grève des cheminots contre la direction de la SNCF (et plus largement contre une mesure du gouvernement) ; la direction de la SNCF a tout intérêt à minimiser le succès de la grève, pour décourager les cheminots et rassurer les usagers.

Part de marché

Quelles sont (dans l’ordre) les trois premières marques de smartphones en fonction de leur part de marché ?

D’après une conférence de presse d’Apple (laquelle ?), repéré par Vandy Berten.

La 3D donne l’impression que la section verte est plus grosse que la violette, mais c’est l’inverse qui est vrai.
D’une manière générale : ne jamais utiliser de 3D dans les graphiques : c’est joli, mais ça fausse très souvent les résultats.

Évolution de la fréquentation des cinémas

La démocratisation d’internet en France (à partir des années 2000) a-t-elle eu un effet négatif/neutre/positif sur la fréquentation des français au cinéma ?

Source : CNC, compilées par Wikipédia.

Les personnes luttant contre le téléchargement illégal affirment souvent que le « piratage » tue le cinéma. Ces données le prouvent-elles ?
Si l’on regarde le premier graphique, qui ne présente que les données sur la période 2001—2007, on a l’impression que la fréquentation stagne, voire décroît. En revanche, en regardant les données depuis les années 50 (second graphique), on voit que la fréquentation a plutôt tendance à augmenter ces dernières années.
Ici, selon la période de temps présentée, on montre un effet ou son contraire.

Aires de disques

En regardant le premier graphique :

Le disque rose est « combien de fois » plus grand que le disque vert ?
Quel pourcentage représente-t-il ?

Source : Le Monde, édition du 12 juin 2012.

Les rayons des cercles sont proportionnels aux pourcentages, mais les aires donnent du coup une impression faussée. Si les rayons des cercles rose et vert sont proportionnels aux pourcentage (environ six fois plus grand), les aires ne le sont pas : l’aire du disque rose est 36 fois celle du disque vert.
Il y a deux problèmes ici.

D’une part, sur un graphique en deux dimensions (comme ici) ou en trois dimensions, une multiplication de l’échelle par deux produit une multiplication de l’aire par 4, et du volume par 8, ce qui est trompeur (attention donc aux graphiques qui, par exemple, pour représenter l’évolution des dépenses de santé, représentent un hôpital plus ou moins gros : est-ce que l’échelle est proportionnelle aux données, ou le volume ?).
D’autre part, l’œil et le cerveau humains savent bien comparer des distances (hauteur ou longueur), mais ne sont pas bons pour comparer des aires (cité par Vandy Berten dans la partie Confondre surface et taille de son article Comment mentir avec un graphique).

Conclusion : Ne pas utiliser de 2D ou 3D (ou alors faire très attention).

Radicalisation en France

Voir la version sans légende sur laquelle travailler en classe.

Classer les couleurs par nombre de cas signalés.
Quelle est la particularité des départements noirs ?

Deux erreurs faussent cette cartographie :

Le choix des couleurs n’est pas usuel. Le plus souvent, pour montrer une gradation de données, les couleurs utilisées vont du plus clair au plus foncé (exemple), ou suivent plus ou moins le spectre lumineux (exemple). Sur cette carte, comparer deux départements sans se référer à la légende n’est pas évident.
Les données représentées sont des données brutes, et non pas relatives. Ce graphique montre que dans les départements les plus peuplés sont relevés le plus grand nombre de cas de radicalisation, ce qui est tout à fait normal si le taux de radicalisation est indépendant de la géographie (voir une présentation humoristique de ce problème).

Tract électoral

Quel procédé a été utilisé pour renforcer l’argument de ce tract électoral ?

L’échelle verticale ne commence pas à 0.

Chiffres de la délinquance

En quoi l’utilisation du graphique par Brice Hortefeux (alors ministre de l’intérieur, donc en charge de la délinquance) est-elle fallacieuse ?

Source : Journal télévisé du 20 janvier 2011, TF1 (repéré par le Cortecs).

Un premier problème classique est que l’échelle verticale est absente. Il est assez facile d’observer qu’elle ne commence pas à zéro.
Le titre est particulièrement vague : Qu’est-ce qui est mesuré ici ? La délinquance réelle ? Le nombre de plaintes ? On a vu des policiers jouer avec les chiffres (faire déposer une plainte par personne à un groupe de personnes pour augmenter ces chiffres ; requalifier une tentative de cambriolage en destruction de biens pour transformer un crime en délit). Les violences interpersonnelles (violences conjugales par exemple) semblent augmenter, mais c’est plutôt dû au fait que les victimes portent maintenant plus souvent plainte (pour une analyse plus approfondie, voir cet article écrit en réaction à ces annonces de Brice Hortefeux). Le nombre de plaintes n’est donc pas un bon indicateur de la délinquance.Est-ce la délinquance ressentie qui est mesurée ? Celle-ci augmente plutôt, alors que le monde n’a jamais été aussi peu violent.Bref, avec assez peu de rigeur (ou beaucoup de mauvaise foi), il est possible de faire dire à peu près n’importe quoi aux chiffres de la délinquance.

Production industrielle

Pouvez-vous classer les quatre pays représentés en fonction de leur production industrielle en 2015 ?

Source : Débat télévisé du 20 mars 2017 (durant la campagne pour l’élection présidentielle). Marine Le Pen a publié ce graphique sur son compte Twitter.

Ce classement n’est pas celui représenté sur le graphique qui représente des indices, base 100 en 2001 (année d’introduction de l’euro). En choisissant une autre année de référence, on obtient des graphiques dans lesquels l’effet annoncé par Marine Le Pen, s’il est toujours présent, est beaucoup moins impressionnant.
Les « décodeurs » du Monde font une analyse détaillée de ce graphique.

Corrélation n’est pas causalité 1

Quel est le lien entre le nombre de magasin Ikéa dans chaque pays, et son nombre de prix Nobel ?

Commençons par remarquer que j’ai supprimé de ce graphique les données qui ne servaient pas mon propos (comme la Chine, qui a beaucoup de prix Nobel, mais peu de magasin Ikéa).
Une règle bien connue des zététiciens est « Corrélation n’est pas causalité ». Il est probable que le nombre de magasins Ikéa dans un pays soit corrélé au nombre de prix Nobel, mais ce n’est pas pour autant que l’un est la cause de l’autre. Dans ce cas, il y a sans doute un troisième facteur qui est la cause de cette corrélation : le niveau de vie. Plus le niveau de vie d’un pays est élevé, plus il y aura de magasin Ikéa et de prix Nobel.
Un autre exemple célèbre est que dans les écoles, la taille des pieds (la pointure) est corrélée au niveau de lecture : en général, les élèves qui ont les plus grands pieds savent mieux lire que les autres. Bien qu’étrange à première vue, ce lien est parfaitement normal : les élèves plus agés ont des pieds plus grands, et savent mieux lire.
Conclusion : Ce n’est pas parce que deux mesures sont liées que l’une est la cause de l’autre.

Corrélation n’est pas causalité 2

Quel est le lien entre le nombre de divorces dans le Maine (un état américain) et la consommation de margarine (aux États-Unis ?) ?

Encore une fois, corrélation n’est pas causalité. Mais cette fois-ci, contrairement à l’exemple précédent, il n’y a sans doute pas de liens entre les deux séries de données : ce n’est probablement qu’un hasard.
Les zététiciens disent également que « L’improbable est probable ». S’il est quasiment impossible que deux séries statistiques prises au hasard soient corrélées, il est tout à fait normal que, parmi les milliards de séries statistiques qui existent dans le monde, plusieurs séries sans lien entre elles varient de la même manière. C’est ce qui se passe ici.

Variations et Valeurs cumulatives

Je n’ai pas utilisé cet exemple avec mes élèves, mais en utilisant les valeurs cumulatives plutôt que les valeurs absolues, il est possible de donner une impression fausse. Vandy Berten donne un exemple dans Comment mentir avec un graphique.

Bibliographie

J’ai puisé mes exemples de graphiques trompeurs dans les articles suivants (mais pas uniquement).

Nicolas Gauvrit : Graphiques, attention aux axes !
Denis Caroti, Alain Le Métayer, Guillemette Reviron : Mathématiques – Comment tromper avec des graphiques.
Vandy Berten : Comment mentir avec un graphique.
Mathilde Damgé : Sept conseils pour ne pas se faire avoir par les représentations graphiques.
Étienne Ghys : Graphiques frelatés.

Sondages d'opinion – Attention à l'intention

21 avril 201820 mai 2020 Guillemette Reviron

Vraiment, un grand merci à Fabien Tessereau, enseignant de mathématiques au collège du Mourion à Villeneuve-lez-Avignon, pour ce retour d’expérience sur un travail d’analyse critique de sondages d’opinion, mené en classe de 4ème. C’est toujours un plaisir de voir qu’on peut enseigner à repérer des biais méthodologiques importants, de manière ludique, y compris avec un public jeune.

Sondages d’opinion : attention à l’intention !

Dans le cadre de la réforme du collège, nous avons projeté de monter en 4ème un Enseignement pratique interdisciplinaire (EPI) sur l’esprit critique avec mes collègues de français et d’histoire – géographie – EMC (enseignement moral et civique). Dans ce cadre, je me suis inscrit à un stage du Plan académique de formation (PAF) dont le thème était « Médias et esprit critique » mené par Guillemette Reviron du collectif « CORTECS ». C’est lors de ce stage qu’elle m’a donné l’idée de travailler avec les élèves sur les limites des sondages d’opinion en leur faisant construire une enquête sur la qualité de la cantine avec la consigne d’utiliser tous les biais possibles dans le recueil des données – mais sans modifier a posteriori ces données – pour que les résultats viennent confirmer une conclusion fixée préalablement. À notre connaissance, ce type de séquence pédagogique n’avait jamais été testée et le résultat n’était pas garanti. J’ai assumé la « prise de risque » et me suis lancé dans la mise en œuvre de cette idée en utilisant les différentes ressources présentées pendant le stage.

Séance 1 – Introduction

Diagrammes et graphiques

Dans mon cours sur les statistiques et la production de graphiques, j’ai intégré une première heure sur la sensibilisation au fait que les graphiques ne sont pas « neutres », même lorsqu’ils sont mathématiquement justes. L’objectif de cette première séance était de les sensibiliser au fait qu’un graphique ne donne pas seulement un résultat mathématique mais qu’il laisse aussi des impressions, et que celles-ci peuvent être orientées différemment par des représentations distinctes d’un même jeu de données. Après une introduction très courte, je leur ai présenté un extrait du journal télévisé de TF1 (20 janvier 2011) où Brice Hortefeux, alors ministre de l’intérieur, présente un diagramme sur l’évolution de la délinquance.

Ensuite, j’ai mis la vidéo en pause sur l’image du ministre présentant le graphique et j’ai demandé aux élèves de me décrire ce qu’ils voyaient. Au terme de l’échange – parfois relancé par mes questions – les élèves avaient pointé plusieurs choses sur la mise en forme : il est apparu que la couleur rouge avait été choisie pour la hausse de la délinquance et le vert pour la baisse. Les élèves ont réussi à analyser que le rouge est une couleur plutôt associée à ce qui n’est « pas bien » ou « interdit » contrairement au vert. Il a aussi été noté que les nombres en vert étaient écrits plus gros pour ressortir. Mais le principal argument mathématique n’est pas venu : aucun élève n’a remarqué l’absence d’échelle sur l’axe des ordonnées (si bien que l’on ne sait pas quels sont les nombres associés à la hauteur des rectangles), nous ne disposons donc que de pourcentages sans valeurs absolues ni ordre de grandeur. Cela pose pourtant au moins deux problèmes : 1) l’augmentation ou la diminution, qui peut paraître importante en pourcentage, peut en fait concerner un nombre très faible de délits, significatif statistiquement mais pas du tout d’un point de vue sociétal ; 2) l’impression d’augmentation ou de diminution peut être faussée si l’axe des ordonnées n’est pas gradué de manière régulière (de 5 en 5 par exemple), ce que nous ne pouvons pas vérifier ici.
Tout ce travail s’est fait à l’oral, en prenant la précaution de préciser que l’objectif n’était pas d’évaluer la pertinence du fond du propos (sur lequel il y aurait par ailleurs beaucoup à dire), mais de travailler sur sa mise en forme ; je notais simplement au tableau les différentes remarques.

J’avais prévu que les élèves ne remarqueraient pas l’absence de ces informations pourtant essentielles, et pour leur faire ressentir l’importance de préciser l’échelle sur les axes, j’ai choisi d’enchaîner avec la vidéo de Nicolas Gauvrit enregistrée pour le Cortecs.

La vidéo étant un peu longue (9 minutes), j’ai surtout fait des arrêts sur images sur les premiers diagrammes présentés (évolution de la délinquance et remboursement des médicaments) ; nous n’avons pas regardé la dernière partie trop complexe pour des élèves de 4ème. Pour chaque graphique, les élèves ont détaillé à l’oral ce qu’ils voyaient et leurs impressions. Ils se sont rendu compte de l’importance des axes, de la graduation choisie et donc de l’échelle utilisée. J’ai fait le rapprochement avec le dessin ou la peinture, quand l’artiste « représente » ce qu’il voit ou ce qu’il imagine (par exemple pour le tableau « Les Ménines » vu par Velasquez ou par Picasso). Il laisse ainsi une « impression » à ceux qui viennent voir l’œuvre. Nous avons alors repris le diagramme du journal de TF1, ils ont immédiatement remarqué qu’il manquait l’échelle et la légende sur l’axe des ordonnées. Là encore, nous avons conclu qu’il manquait des informations mathématiques, que cette omission était susceptible d’orienter notre jugement et que les couleurs choisies pouvaient avoir de l’importance. Les élèves ont très bien réagi à cette première partie en étant très actifs, même les moins à l’aise en mathématiques, les questions de description étant relativement simples et accessibles à tous.

Nous avons ensuite visionné un extrait du Petit journal de Canal+ (29 novembre 2011) qui compare les graphiques de l’évolution du chômage présentés le même jour par trois journaux télévisés différents : ceux de TF1, France 2 et France 3 sur un ton humoristique.

Nous en avons retenu que pour une même information, les trois graphiques – justes mathématiquement – ne laissaient pas la même impression.

Nous avons enchaîné sur un diaporama que j’ai réalisé à partir du travail d’Alain le Métayer sur le site du Cortecs sur les diagrammes en araignée des conseils de classe. Suivant l’ordre des matières sur la toile, les impressions données par les trois diagrammes sont différentes et pourtant les valeurs mathématiques sont exactement les mêmes. Là encore, les élèves ont très bien réagi, le but étant qu’ils se posent des questions et qu’ils doutent, sans tomber dans l’excès « Tout le monde nous ment ! ». J’ai bien insisté à chaque fois sur le fait de lire attentivement les éléments mathématiques et de faire attention aux impressions éventuellement données.

Tri sélectif des données et enquêtes d’opinion : les écueils du micro-trottoir

Nous avons ensuite réfléchi à la notion d’esprit critique dans le journalisme en visionnant un dernier extrait vidéo du Petit journal de Canal + (13 juin 2013).

On voit dans cette vidéo un micro-trottoir réalisé dans une gare parisienne un jour de grève des agents de la SNCF. Dans une première partie, les clients interrogés semblent particulièrement mécontents. Dans une deuxième partie, on voit les mêmes personnes bien plus nuancées voire même compréhensives envers les agents grévistes. Cela met en avant le fait que l’on peut fabriquer un point de vue en n’utilisant qu’une partie des réponses des personnes interrogées (c’est une illustration du tri sélectif des données). Les élèves ont été aussi bien surpris que choqués et ont vraiment pris conscience qu’un micro-trottoir, fruit d’une sélection de témoignages, peut être orienté dans un sens ou dans un autre. Toujours à l’oral, nous avons essayé de trouver un intérêt à ce reportage ; nous en sommes arrivés à questionner la pertinence du lieu utilisé pour réaliser le micro-trottoir. Nous sommes parvenus à la conclusion qu’en effet, à la gare un jour de grève, il y avait de grandes chances que les personnes présentes soient essentiellement celles qui n’étaient pas au courant de la grève, ou alors celles qui n’avaient pu faire autrement pour se déplacer, donc des gens probablement mécontents dans tous les cas (deuxième tri sélectif des données). J’ai saisi cette occasion pour parler d’échantillon représentatif.

Présentation du projet

Après ces réflexions, je leur ai présenté le projet : la classe serait divisée en deux groupes pour concevoir une enquête de satisfaction sur la cantine au sein du collège. Un groupe serait chargé de « s’arranger » pour que le recueil de données conduise à conclure que les élèves du collège apprécient la cantine, tandis que l’autre devrait « s’arranger » pour conclure l’inverse en jouant uniquement sur le mode de recueil des données mais en les traitant avec rigueur. La plupart des élèves se sont montrés immédiatement très motivés et investis. La classe a été répartie en deux groupes et chaque groupe a commencé à réfléchir chez soi, pour préparer la deuxième séance, à sa stratégie.

Séance 2 – Préparation de l’enquête

Pendant cette deuxième heure, un groupe est resté avec moi et l’autre groupe est allé réfléchir avec un collègue. Le but pour chaque groupe était de trouver les moyens d’arriver à sa fin. Nous avons réuni les deux groupes pour une mise en commun pour les dix dernières minutes. Il a été très intéressant de constater que les deux groupes ont choisi la même question : « qu’as-tu pensé du repas de la cantine aujourd’hui ? » (De son côté, le professeur de français travaillait avec les élèves sur les différentes façons de poser une même question mais pouvant aboutir à des réponses différentes pour une même personne interrogée).
Chaque groupe a décidé de proposer des réponses au choix (nous avions déjà vu dans un exercice qu’il pouvait être difficile pour le dépouillement de laisser les gens répondre ce qu’ils voulaient). Le groupe ayant pour mission d’obtenir une réponse positive a opté pour trois réponses au choix : 1 – Très Satisfaisant ; 2 – Plutôt satisfaisant ; 3 – Pas du tout satisfaisant. L’autre groupe a choisi quatre réponse au choix : 1 – Excellent ; 2 – Satisfaisant ; 3 – Plutôt pas satisfaisant ; 4 – Pas du tout satisfaisant.
Pour le groupe dont j’ai eu la charge, je les ai laissé réfléchir entre eux sans intervenir pendant 10 minutes puis j’ai lancé quelques questions afin d’arriver à ce résultat. Comme leur but était de récupérer dans sa partie les personnes répondant plutôt au milieu (dans le plus ou le moins suivant le cas), la question s’est alors posée de savoir : qui interroger, où, et comment choisir les personnes interrogées ? Très rapidement la question du menu est arrivée – est-il prévu des épinards ou des frites ? Ensuite un élève a proposé d’interroger les élèves à la sortie du self à côté du tapis roulant où l’on dépose les plateaux : on ciblerait, suivant le groupe, les élèves dont le plateau déposé serait vide ou plein. Pour des questions d’organisation, je leur ai dit qu’ils ne pouvaient pas être plus de trois par jour à questionner leurs camarades. Enfin, le collège comptant 800 élèves, il a été décidé que chaque élève devait en interroger au moins 8 pour avoir environ 100 résultats pour chacune des deux versions de l’enquête. Afin d’être sûr de toucher un peu tous les élèves du collège, une deuxième question sur le niveau de l’élève a été ajoutée.

Séance 3 – Enquête et dépouillement

L’heure suivante, j’avais préparé dix questionnaires pour chacun (tous sur une même page pour des questions pratiques) et apporté les menus du mois suivant. Les élèves se sont alors répartis par groupe de 2 ou 3 sur les jours où ils allaient poser les questions en fonction des plats (la désignation des « bons » et des « mauvais » menus s’est faite sur des bases entièrement subjectives). Le recueil des données a duré un mois. Six élèves n’ont pas fait passer l’enquête par oubli ou par manque d’envie ou encore par timidité. À l’issue de cette collecte, trois élèves de chaque groupe ont dépouillé les réponses obtenues. Les tableaux avec les résultats ont été distribués à chacun (en fonction de son groupe de départ) et chaque élève a pu réaliser, grâce à l’assistant graphique du tableur, un diagramme circulaire avec les résultats obtenus. Et quels résultats ! Chaque groupe a en effet parfaitement réussi à obtenir les résultats attendus dès le départ. Un élève a aussi proposé de mettre en vert les réponses « positives » et en rouge les réponses « négatives » afin de voir le contraste entre les deux diagrammes. Nous avions donc une enquête sur la cantine rigoureuse sur le plan mathématique mais qui donnait deux résultats complètement différents.

Cortecs_Fabien Tessereau_Sondage_cantine_Non

Cortecs_Fabien Tessereau_Sondage_cantine_Oui

Cortecs_Fabien Tessereau_Sondage_cantine_donnees

Bilan

De façon générale sur l’ensemble du projet, les élèves ont été très motivés pour participer et le fait de pouvoir « manipuler » des résultats leur a beaucoup plu. Nous avons bien sûr aussi parlé du fait qu’ils pouvaient du coup, eux aussi être manipulés, malgré l’utilisation des mathématiques. Il nous a manqué du temps en fin d’année pour réaliser un panneau d’affichage avec les deux représentations graphiques sur la même page, mais c’est en projet pour cette année : même si les élèves sont en 3°. Cet esprit critique sur les statistiques me paraissant important, j’ai maintenant intégré à mon chapitre sur les statistiques la première heure de cours de ce projet (avec les vidéos) avec une trace écrite en plus.

Fabien Tessereau

Les TPEc : travaux personnels encadrés critiques et démarche d'investigation en classe de première

10 février 201820 mai 2020 Julien Peccoud

Nous sommes nombreux·ses, pour les plus jeunes d’entre nous, à avoir enduré l’épreuve des TPE (Travaux Personnels Encadrés) en classe de première générale. Beaucoup y traînent des pieds, certain·e·s s’investissent énormément mais dans tous les cas on ne retrouve souvent que des lieux communs, des sujets un peu « classiques » qui amènent souvent les élèves à recopier ou reformuler des TPE des années précédentes trouvés sur le Web. Sachant que cet enseignement est le lieu d’une grande liberté pour les élèves, cela faisait un certain temps que je pensais y insuffler de la pensée critique dans le but de développer la démarche scientifique de manière concrète et atteignable. Voici quelques propositions pour quiconque aura envie de s’amuser un peu en TPE.

Le contexte

Les TPE constituent une épreuve du baccalauréat lors de laquelle les élèves doivent réaliser une démarche de groupe afin de répondre ou tenter de répondre à une problématique de leur cru. L’évaluation se fait suivant trois composantes : le suivi par les enseignant·e·s qui encadrent le TPE pendant la moitié de l’année, la production du groupe et l’oral (sorte de soutenance de la production). Les TPE sont présents pour les séries L, ES et S en première et constituent une épreuve anticipée du bac.

Les élèves doivent trouver un thème d’étude et poser une problématique à laquelle ils devront tenter de répondre par une recherche documentaire, par des expérimentations, par des rencontres de professionnel·les, visites et autres questionnaires.

La production peut prendre la forme d’un dossier, d’un site Web, d’une vidéo, d’un magazine, d’une exposition… bref, tout est permis ! Leur sujet doit normalement tomber dans un des six thèmes nationaux proposés par le Ministère (au passage, on pourra se délecter critiquement de ce nouveau thème sorti cette année, commun aux trois séries et totalement dans l’ère Macron¹). Ces thèmes étant très larges, on peut donc avoir une certaine liberté d’action. Enfin, les TPE sont encadrés par plusieurs enseignant·e·s de matières différentes et les élèves doivent traiter un sujet faisant intervenir au moins deux matières.

Pourquoi les TPE ?

Pour ma part, étant enseignant de SVT (Sciences de la vie et de la Terre), j’ai suivi des élèves de 1ère S. Je pense que l’on peut proposer des thèmes de pensée critique dans les autres filières (ES et L) même si la démarche et la problématisation sont légèrement différentes. Tout cela part d’un constat souvent partagé entre filières : les élèves trouvent des thèmes d’étude un peu « bateau » et aboutissent à des problématiques n’amenant qu’à un « simple » exposé et non à une démarche de recherche originale. L’intérêt pour les élèves est donc de pouvoir trouver une problématique n’amenant pas une réponse « directe » mais ouvrant vers une réelle recherche personnelle. C’est là où j’y vois un intérêt pour la pensée critique et particulièrement pour la démarche zététique qui est un bon marche-pied pour développer l’enseignement de la démarche expérimentale et la recherche de preuves. En effet, trouver des sujets d’études peu étudiés, stimulants, pris dans les controverses scientifiques ou les sujets-frontières entre science et croyance… permet aux élèves de mettre en place une réelle démarche d’investigation où ils·elles pourront tester et vérifier des affirmations de type scientifique.

Un cheval de Troie

En théorie, les enseignant·e·s ne sont pas sensés orienter les élèves sur tel ou tel sujet. Mais c’est là que le bât blesse (cf. plus haut) et je me suis mis en tête de leur proposer de travailler sur des thèmes liés au paranormal, aux phénomènes étranges, aux thérapies dites alternatives et croyances sociales. Pour des 1ère S, cela est orienté vers la démarche scientifique mais j’imagine déjà pas mal de thèmes pour les ES et les L (la condition animale, le genre, les conflits d’intérêts, la main invisible du marché, la répartition des pouvoirs dans un établissement scolaire, etc…). J’ai donc décidé de les orienter plus ou moins implicitement sur des sujets de cet ordre.

La démarche

Au final, je n’ai pas produit énormément de matériel pédagogique étant donné que les TPE sont essentiellement du travail personnel des élèves. Les premières séances sont généralement dédiées à l’explication des TPE, la notion de problématique et les bases de la recherche documentaire. J’en ai donc profité pour faire une séance autour de la démarche scientifique et de la problématique pour influer des notions de zététique.

Nous étions en charge, avec mes trois collègues, de deux classes de 1ère S. L’équipe était constituée d’un enseignant de physique-chimie, d’un enseignant de mathématiques, et de deux enseignant·e·s de SVT. Nous avons procédé à une première séance lors de laquelle nous avons présenté les TPE et avons laissé les élèves parcourir les thèmes nationaux et commencer à trouver un thème d’étude. Dès la deuxième séance, nous avons scindé le groupe (environ 60 élèves) en trois sous-groupes qui allaient tourner sur trois ateliers pendant trois heures. Pendant qu’un groupe était en recherche libre, l’autre était avec la documentaliste pour une formation à la recherche documentaire et le dernier groupe était avec moi pour une présentation zététique / démarche scientifique / problématique.

La présentation

La présentation se développe selon trois grands axes :

Une partie plutôt basée sur de l’épistémologie, et j’y développe la notion d’affirmation de type scientifique pour enchaîner sur le distinguo acte de foi vs. remport d’adhésion permettant d’amener au statut du témoignage et enfin à l’explication alternative (et donc le rasoir d’occam)
Une partie permettant de présenter les thèmes liés à la zététique en parcourant des choses comme l’archéo-fiction, la cryptozoologie, les pouvoirs du corps et les médecines dites alternatives. Je finis par la perception des probabilités pour arriver à l’idée que le « bizarre est probable »
Une dernière partie qui devrait prendre 30 minutes et qui s’intéresse à la démarche scientifique avec la notion de reproductibilité, le témoin, la taille et la représentativité de l’échantillon, l’aveugle et le double aveugle en finissant sur l’effet paillasson pour bien leur faire comprendre qu’ils·elles doivent travailler sur un sujet précis possédant une seule assertion dans le langage commun.

L’objectif de tout cela est de leur faire insuffler l’idée de trouver un sujet intriguant sur lequel ils·elles exercent leur curiosité et se fassent plaisir notamment à trouver des protocoles originaux.

J’insiste sur le fait qu’un « bon » TPE doit comporter des expérimentations mais pour ne pas leur faire trop peur, je leur dis aussi qu’un TPE avec une recherche documentaire solide qui croise des informations ou basé sur des analyses de données (épidémiologie par exemple) est tout aussi satisfaisant.

Je leur ai ensuite mis sur le réseau du lycée un document avec une multitude de thèmes issus des sujets traités par les étudiant·e·s de l’enseignement zététique de Richard Monvoisin sur plusieurs années ainsi que certains sujets proposés par Guillemette Reviron ou même cette magnifique page wikipédia sur les médecines non conventionnelles que m’a proposé Nelly Darbois.

Le matériel utilisé

Pour un peu plus de détail, voici le déroulé de la présentation avec les quelques vidéos que j’ai pu utiliser. La présentation est téléchargeable sous licence CC-by-SA :

– Au format diaporama LibreOffice

– Au format PDF

Je l’ai laissée telle quelle, mais il faut enlever des parties (voir plus bas, les erreurs commises).

Je questionne les élèves sur ce que leur renvoie le terme « science » pour proposer les quatre définitions du mot « science » et insister sur le fait que je ne parlerai que de la démarche scientifique.

Je présente quelques types d’informations/affirmations en donnant des exemples pour chaque pour ensuite arriver sur la particularité des affirmations de type scientifique. Je demande ensuite ce qui distingue une affirmation scientifique des autres types d’affirmation. J’ai pu remarquer que les élèves avaient de grandes facilités pour dire que l’affirmation scientifique est « testable ». Je donne ensuite quelques exemples d’affirmations de type scientifique (une pub de médium, des recettes de cuisine, du soin par magnétisme).

Cela nous amène à la notion du statut du témoignage et à la maxime de Hume. Cela permet de leur faire comprendre qu’un témoignage récolté n’est pas une preuve dans leur TPE mais aussi qu’ils·elles peuvent se baser sur un témoignage extraordinaire pour commencer à rechercher des preuves solides à ce témoignage.

On arrive tout doucement au rasoir d’Occam : face à un témoignage et une explication coûteuse à un phénomène, il est de logique d’épuiser d’abord les hypothèses alternatives moins coûteuses. Je présente une situation bizarre (un caribou pendu sur les fils d’un poteau électrique²) pour leur faire sortir des hypothèses puis leur donne la réponse³.

Je leur montre cette vidéo qui est sensée démontrer par l’humour cette notion du rasoir d’Occam mais au vu du peu de réactions de la part des élèves, je pense qu’il faut peut-être en trouver une autre. Richard Monvoisin me suggère d’utiliser la vidéo de Jeanne d’Arc présente sur cet article relatif au rasoir d’Occam. Un très bon épisode de Kaamellot existe également mais nous avons du le supprimer, voir l’article en question.

Je leur présente ensuite le cas des combustions humaines dites « spontanées »⁴ pour leur donner une idée de recherche d’explications scientifiques et cognitivement peu coûteuses.

Vient ensuite la présentation de divers thèmes de zététique (cryptozoologie, thérapies alternatives, archéo-fiction, pouvoirs du corps…).

Je fais un petit laïus sur le perceptions des probabilités à partir de la séquence suivante que j’ai montée à partir de différentes vidéos sur le Web. Cela me permet d’insister sur le tri des données (cette vidéo est un peu longue et on peut passer un peu plus rapidement à certains moments).

Télécharger

Cela permet de faire le lien avec les faits « extraordinaires ». Je commence avec cette vidéo mythique de la tourterelle explosant en plein vol suite à un lancer de Randy Johnson, le 24 mars 2001.

Télécharger

Les « miracles » de Lourdes permettent d’aborder la question de l’extraordinarité : des guérisons extraordinaires se produisent-elles à Lourdes, et si oui, se réalisent-elles à un taux supérieur à tout autre endroit, aux hôpitaux publics par exemple ? ⁵ Cela permet de montrer que le « bizarre est probable » et de leur faire prendre du recul sur les chiffres qu’ils·elles peuvent trouver, de les mettre en perspective d’une situation.

À partir de là, je développe les outils de la démarche expérimentale en commençant par la simple reproductibilité en me basant sur cette vidéo de catalepsie de spectacle par Franck Syx (je n’ai pas le temps de la reproduire mais je leur dis qu’on pourra essayer après la séance si ça leur dit) :

Télécharger

Je ne développe pas les autres (témoin, aveugle et double aveugle, taille et représentativité de l’échantillon) car l’idée reste la même : leur présenter des protocoles inventées et méthodologiquement problématiques pour qu’ils·elles puissent lever le problème et comprendre comment on peut « objectiver » des données récoltées.

Je finis enfin par présenter l’effet paillasson car c’est un vrai problème dans la rédaction des problématiques en TPE : les élèves doivent restreindre leur recherche et ont tendance à placer des mots trop vagues ou ayant des définitions diverses et variées (les termes « énergie », « mémoire », « cerveau » ou « préserver l’environnement » en sont des exemples classiques). J’ai utilisé les cartes de thérapeutes d’un festival récent sur Grenoble, FestiZen, qui regorge d’effets paillasson et d’effets puits.

Les erreurs commises

J’ai vu un peu gros pour le format 1h et sur les deux premiers groupes je n’ai pas eu le temps de traiter correctement la dernière partie, pourtant essentielle. J’ai donc réduit pour le dernier groupe et c’était vraiment mieux. Je n’ai donc pas traité la définition de « science », l’épistémologie « critique » (matérialisme méthodologique, scepticisme, rationalité) ni acte de foi vs. remport d’adhésion. L’ensemble reste un peu chargé mais cela rentre en une heure

La suite…

Pour la suite des TPE, c’est surtout de l’improvisation. Nous, les enseignant·e·s, devons être présent·e·s pour répondre aux questions des élèves et leur éviter de partir sur des fausses pistes ou sur des sujets trop complexes en terme de notions pour leur niveau. Il faut faire en sorte que le sujet soit assez fécond (possibilité de tester, de reproduire, de vérifier, de trouver de l’information…) mais assez restreint pour pouvoir travailler sur un paramètre bien identifié.

En cette fin de TPE, il est temps de dresser un bilan. C’est un peu triste au final car sur les 20 groupes constitués, seulement 5 ont travaillé sur un sujet critique :

Le triangle des Bermudes (sujet « classique »)
Les personnes se disant électrosensibles sont-elles capables de détecter la présence de Wifi en expérimentation contrôlée ? Malheureusement, le groupe s’est retrouvé face à la difficulté sociale : il n’a pas pu trouver une seule personne se disant électrosensible voulant bien se prêter au jeu de l’expérimentation.
Le scénario catastrophe du film « Le Jour d’après » dans lequel le Gulf Stream subit un dérèglement est-il scientifiquement plausible ?
La spiruline : petite déception, les élèves n’ont pas vraiment pris l’angle critique, étant déjà convaincues par les bienfaits de cette algue à la mode. C’est dommage, c’était un sujet fécond avec multiples problématiques possibles
Les magnétiseurs : groupe très stimulant ! Réalisation d’un protocole expérimental réalisé en collaboration avec un magnétiseur venu au lycée pour réaliser l’expérience. Juste pour ce groupe, je suis content d’avoir mis de l’énergie (c’est le cas de le dire) dans ce travail de TPE.

L'effet Will Rogers, ou effet de migration des stades

19 septembre 201620 mai 2020 Richard Monvoisin

L’effet de migration des stades (stage migration en anglais), ou effet Will Rogers, en hommage à l’acteur du même nom qui aurait déclaré « quand les Okies ⁵⁰ quittèrent l’Oklahoma et vinrent en Californie, ils élevèrent l’intelligence moyenne des deux côtés ».

En déplaçant un élément d’un groupe à l’autre, on peut paradoxalement faire monter la moyenne dans… les deux groupes ! Représentons-nous par exemple un ensemble de patients qui indiquent sur une échelle de 1 à 10 la douleur moyenne qu’ils
ressentent. On crée un groupe A à douleur faible, A = {1, 2, 3, 4} et
un groupe B de douleur forte, à partir de 5, soit B = {5, 6, 7, 8, 9}

Si l’on fait la moyenne de chaque groupe, on obtiendra 2,5 pour A,
et 7 pour B.

Mais imaginons que les normes d’inclusion changent, et que par exemple, après une recommandation de l’Organisation mondiale de la Santé, 5 est finalement considéré comme faible. Les groupes deviennent alors A = {1, 2, 3, 4, 5} et B = {6, 7, 8, 9}. Or
de ce fait, la moyenne (notée ci-dessous μ) de A est montée à 3, et celle de B, à 7,5. Les deux groupes ont vu leur moyenne augmenter.

Situation 1
A = {1, 2, 3, 4} -> μ = 2,5
B = {5, 6, 7, 8, 9} -> μ = 7

Situation 2
A = {1, 2, 3, 4, 5} -> μ = 3
B = {6, 7, 8, 9} -> μ = 7,5

Quelles en sont les conséquences ? Si le système de détection d’une maladie par exemple s’améliore et permet du dépistage précoce, certains individus passeront du groupe des sujets en bonne santé vers le groupe des sujets malades. À travers ce changement, la moyenne de la durée de vie augmentera paradoxalement dans les deux groupes, et cela quel que soit le traitement que l’on fera. On aura ainsi tendance à conclure à l’efficacité du traitement, alors que c’est un problème d’un critère d’inclusion dans les groupes qui a changé ⁵¹.

Nicolas Pinsault, Richard Monvoisin

(tiré de Tout ce que vous n’avez jamais voulu savoir sur les thérapies manuelles, aux éditions PUG).

On trouvera un autre exemple dans « Le dépistage organisé du cancer du sein : outils d’autodéfense intellectuelle » de N. Darbois et G. Reviron.

Scénarios complotistes et autodéfense intellectuelle : comment exercer son esprit critique ? (suite)

29 juin 201613 mai 2020 Denis Caroti et Guillemette Reviron

Dans le cadre de nos enseignements et conférences, nous sommes régulièrement sollicités pour fournir des outils d’analyse des scénarios complotistes, notamment en raison des mécanismes et biais qui contribuent à rendre ces scénarios si séduisants. A l’instar de ce que la métaphore du pêcheur ⁵² suggère, nous sommes convaincus qu’il est plus utile de fournir au public des outils et des techniques permettant de faire la distinction entre recherche scientifique sur les complots et conspirationnisme peu étayé, plutôt que de se borner à déconstruire les quelques scénarios complotistes en vogue.

Nous avons expliqué en détail la progression que nous suivions pour aborder ces questions ici. Cet article, publié dans les Cahiers Pédagogiques¹, développe plus précisément nos outils pédagogiques pour analyser les arguments probabilistes souvent utilisés dans les thèses conspirationnistes.

Coïncidences et scénarios conspirationnistes

De nombreux enseignants sont confrontés à des élèves qui adhèrent à des scénarios conspirationnistes peu étayés reposant essentiellement sur un ensemble de coïncidences qui leur semblent trop étranges pour n’être dues qu’au hasard. C’est un problème plus profond qu’il n’y paraît. En effet, bien que la proportionnalité, les probabilités et les statistiques soient abordées tout au long de la scolarité, la psychologie cognitive nous apprend que nous n’en restons pas moins sujets à toutes sortes de biais qui rendent très peu fiables nos intuitions concernant les pourcentages et les statistiques. Et ce sont les mêmes erreurs de raisonnement qui nous conduisent à nous amuser d’une coïncidence – j’ai rêvé d’un cousin lointain que je n’ai pas vu depuis 5 ans et il m’a appelé le jour même – aussi bien qu’à nous laisser convaincre par certains argumentaires conspirationnistes reposant uniquement sur la réalisation de faits que l’on pensait pourtant très peu probables.
De ce constat est née l’idée de travailler spécifiquement sur la déconstruction de ces biais, en prenant garde à ne pas laisser entendre qu’un complot est nécessairement une vue de l’esprit. Il existe des complots étayés, et l’objectif est bien d’apprendre à jauger la force ou la faiblesse des arguments avancés pour défendre chaque thèse.

Certaines séquences présentées ci-dessous ont été élaborées pour des étudiants scientifiques (L2) par des membres du Cortecs, mais ont été reprises et adaptées pour des élèves de 6ème et 5ème par des enseignants du secondaire²Merci à M. Margerit, M.-H. Hilaire et V. August pour leurs retours[\ref].

La première étape vise à repérer, analyser et déconstruire quelques arguments aussi courants que fallacieux en partant d’un scénario satirique type « vérité cachée » issue de l’émission Le Before (Canal+) : « Jésus est né en Provence ». Après la projection, les élèves sont invités à recenser les différents arguments avancés pour étayer cette fausse thèse et à discuter de leurs limites. C’est l’occasion d’expliquer

que l’on trouve plus facilement ce qu’on cherche,
que nous sommes tous sujets à de la validation subjective,
qu’il est nécessaire de poser des critères précis pour (in)valider un test (par exemple, si la région PACA est un triangle inversé, à partir de quand valide-t-on qu’une forme géométrique est presque un triangle ? ),
éventuellement, suivant les niveaux, d’expliquer les écueils du raisonnement à rebours,
qu’il est problématique de ne pas s’être assurés que ces coïncidences ne touchaient que la Provence.

Pour favoriser la sérénité des discussions qui peuvent avoir lieu par la suite, il nous semble important de terminer cette étape en prenant quelques précautions : le fait que les arguments soient faibles ne permet pas de conclure que la thèse est fausse. En revanche, rationnellement, il est légitime de demander à un tenant de cette thèse des arguments plus solides, et de revenir sur deux maximes fondamentales : une affirmation extraordinaire nécessite une preuve solide et la charge de la preuve incombe à celui qui prétend.

Coïncidences et vérités cachées

Dans un deuxième temps, pour consolider ce qui vient d’être détaillé et montrer que si on cherche des coïncidences, on en trouve, les élèves se mettent par deux pour un petit concours : chaque paire d’élèves doit recenser le maximum de leurs points communs (nombre de lettres dans leur prénom ou dans le prénom des parents, nombre de frères et sœurs, dates ou mois de naissance, somme des chiffres de la date de naissance, lieu de naissance etc.). En dix minutes, chaque groupe trouve entre dix et vingt points communs…

Pour la séance suivante, les élèves auront pour mission d’écrire leur propre fausse « vérité cachée » qu’ils exposeront aux autres avec, pour consigne, de commencer leur exposé par une phrase résumant la fausse thèse qu’ils prétendent défendre. L’objectif est d’ancrer le fait que, si l’on accepte ce type d’argumentaire, il devient possible de démontrer à peu près tout et n’importe quoi.

Pour approfondir cette séquence, on pourra également travailler plus précisément deux biais cognitifs importants.

Michael Jackson et le nombre 7

Le premier concerne notre sous-estimation de certaines probabilités : ce n’est pas parce qu’un événement nous semble très peu probable qu’il l’est réellement. Partons de l’affirmation « le chiffre de Mickael Jackson est le 7 » et de la tentative de preuve suivante :

Mickael Jackson a signé son testament le 07 07 2002
la cérémonie lui rendant hommage s’est tenue le 07 07 2009 (remarquons à ce propos que 2009 – 2002 = 7)
il était le 7ème enfant d’une famille de 9.
il y a 7 lettres dans son prénom et dans son nom
il est né en 1958 : 19+58=77

Outre tous les biais évoqués dans la première étape, il s’agit ici de se demander s’il est si étonnant que le chiffre 7 apparaisse dans la vie de M. Jackson. Une réplique courante est de comparer cette fréquence d’apparition à celles d’autres chiffres (par exemple 5 ou 3). Nous n’avons en revanche encore jamais rencontré quelqu’un rétorquant spontanément qu’il est tout simplement banal qu’un nombre soit relié à 7. Pourtant, si l’on regarde la liste des nombres de 1 à 400, plus de 42 % d’entre eux ont un lien avec 7 (multiple de 7, commence ou finit par 7, la somme des chiffres est un multiple de 7, la somme théosophique est 7). Ce travail d’identification des nombres reliés à 7 peut être fait par les élèves – en coloriant les cases dans une grille -, quitte à répartir le travail par tranche de 100 nombres. On pourra aussi leur proposer de trouver tous les nombres entre 1 et 100 en lien avec leur chiffre préféré et comparer.

Enfin, ce n’est pas parce qu’un événement a une faible probabilité d’apparition qu’il est impossible qu’il se réalise. Tout dépend en effet du nombre d’essais, de tentatives, de répétitions pour le faire apparaître. Pour comprendre cela, dans une classe d’au moins 32 élèves, nous notons au tableau une chaîne de 5 « pile ou face », puis nous demandons aux élèves de lancer chacun 6 fois d’affilée une pièce en se concentrant sur la combinaison au tableau. Statistiquement, un élève tire la bonne combinaison, mais, pour ne pas être pris au dépourvu, il faut prévoir les rares cas où cet événement ne sera pas réalisé – on pourra émettre l’hypothèse qu’ils n’étaient pas assez concentrés et les faire recommencer. Attention toutefois à prendre le temps de déconstruire ce raisonnement à la fin le cas échéant. L’enseignant anime la discussion qui suit pour expliquer ce « phénomène ».

Afin de complexifier les échanges, on pourra répéter l’expérience et discuter du résultat (est-il probable que ce soit le même élève ? Est-ce impossible ? ) ou faire le même exercice avec une séquence de 10 « pile ou face » au tableau (est-il probable qu’un élève tire la bonne séquence ? Est-ce impossible ? )

Pour conclure, on illustre tout cela sur un cas concret : un extrait vidéo défendant la thèse « Hollywood savait pour les attentats du World Trade Center ».

Ajoutons que ce type de séquence s’adapte facilement pour d’autres niveaux, notamment sur la question des probabilités et des statistiques qui peuvent faire l’objet d’une analyse théorique et pratique plus poussée selon les classes concernées: d’autres séquences sont disponibles sur le site du Cortecs