
L’effet de migration des stades (stage migration en anglais), ou effet Will Rogers, en hommage à l’acteur du même nom qui aurait déclaré « quand les Okies 1 quittèrent l’Oklahoma et vinrent en Californie, ils élevèrent l’intelligence moyenne des deux côtés ».
En déplaçant un élément d’un groupe à l’autre, on peut paradoxalement faire monter la moyenne dans… les deux groupes ! Représentons-nous par exemple un ensemble de patients qui indiquent sur une échelle de 1 à 10 la douleur moyenne qu’ils
ressentent. On crée un groupe A à douleur faible, A = {1, 2, 3, 4} et
un groupe B de douleur forte, à partir de 5, soit B = {5, 6, 7, 8, 9}
Si l’on fait la moyenne de chaque groupe, on obtiendra 2,5 pour A,
et 7 pour B.
Mais imaginons que les normes d’inclusion changent, et que par exemple, après une recommandation de l’Organisation mondiale de la Santé, 5 est finalement considéré comme faible. Les groupes deviennent alors A = {1, 2, 3, 4, 5} et B = {6, 7, 8, 9}. Or
de ce fait, la moyenne (notée ci-dessous μ) de A est montée à 3, et celle de B, à 7,5. Les deux groupes ont vu leur moyenne augmenter.
Situation 1
A = {1, 2, 3, 4} -> μ = 2,5
B = {5, 6, 7, 8, 9} -> μ = 7
Situation 2
A = {1, 2, 3, 4, 5} -> μ = 3
B = {6, 7, 8, 9} -> μ = 7,5
Quelles en sont les conséquences ? Si le système de détection d’une maladie par exemple s’améliore et permet du dépistage précoce, certains individus passeront du groupe des sujets en bonne santé vers le groupe des sujets malades. À travers ce changement, la moyenne de la durée de vie augmentera paradoxalement dans les deux groupes, et cela quel que soit le traitement que l’on fera. On aura ainsi tendance à conclure à l’efficacité du traitement, alors que c’est un problème d’un critère d’inclusion dans les groupes qui a changé 2.
Nicolas Pinsault, Richard Monvoisin
(tiré de Tout ce que vous n’avez jamais voulu savoir sur les thérapies manuelles, aux éditions PUG).
On trouvera un autre exemple dans « Le dépistage organisé du cancer du sein : outils d’autodéfense intellectuelle » de N. Darbois et G. Reviron.































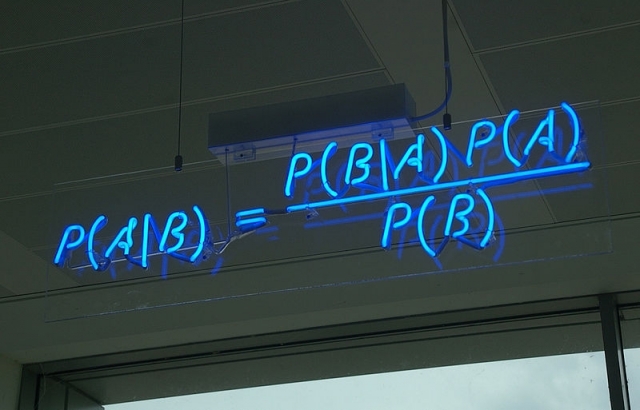

 et d’en déduire que la cause principale de ces cancers est le tabagisme. Attention, si vous en tirez cette conclusion, vous êtes en train de toucher du doigt le problème des probabilités inversées : ce n’est pas cette statistique seule qui permet d’inférer un lien de cause à effet entre tabagisme et cancer. Car on pourrait très bien trouver, en cherchant un peu, que 99% des personnes décédées portaient des sous-vêtements, sans pour autant en conclure à un lien causal direct entre porter un slip et mourir d’un cancer des poumons. Autrement dit, la probabilité de porter des sous-vêtements sachant que l’on est mort d’un cancer ne nous donne aucune information sur la dangerosité ou le risque de cette pratique.
et d’en déduire que la cause principale de ces cancers est le tabagisme. Attention, si vous en tirez cette conclusion, vous êtes en train de toucher du doigt le problème des probabilités inversées : ce n’est pas cette statistique seule qui permet d’inférer un lien de cause à effet entre tabagisme et cancer. Car on pourrait très bien trouver, en cherchant un peu, que 99% des personnes décédées portaient des sous-vêtements, sans pour autant en conclure à un lien causal direct entre porter un slip et mourir d’un cancer des poumons. Autrement dit, la probabilité de porter des sous-vêtements sachant que l’on est mort d’un cancer ne nous donne aucune information sur la dangerosité ou le risque de cette pratique.
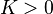 , un flux de capitaux entrant de
, un flux de capitaux entrant de  , un taux de rendement promis
, un taux de rendement promis  et un taux de rendement effectif
et un taux de rendement effectif 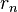 . Si
. Si  alors le fonds est légal et possède un taux de profit de
alors le fonds est légal et possède un taux de profit de  . Si par contre
. Si par contre 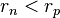 , alors le fonds promet plus d’argent qu’il ne peut en obtenir. Dans ce cas,
, alors le fonds promet plus d’argent qu’il ne peut en obtenir. Dans ce cas, 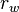 , appliqué à tout temps
, appliqué à tout temps  sur le capital accumulé promis. Le retrait au temps
sur le capital accumulé promis. Le retrait au temps 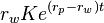 . Il faut aussi ajouter les retraits des investisseurs qui sont arrivés entre le temps
. Il faut aussi ajouter les retraits des investisseurs qui sont arrivés entre le temps  et le temps
et le temps  au temps
au temps  . Le retrait pour ces investisseurs est donc de
. Le retrait pour ces investisseurs est donc de 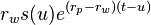 . En intégrant ces retraits entre
. En intégrant ces retraits entre 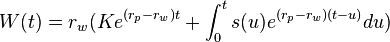
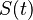 est la valeur du fonds au temps
est la valeur du fonds au temps  est obtenu en ajoutant à
est obtenu en ajoutant à 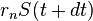 , le flux de capitaux entrant
, le flux de capitaux entrant 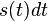 et en soustrayant les retraits
et en soustrayant les retraits 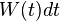 . Nous obtenons donc
. Nous obtenons donc 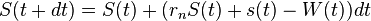 , ce qui conduit à l’équation différentielle linéaire
, ce qui conduit à l’équation différentielle linéaire 
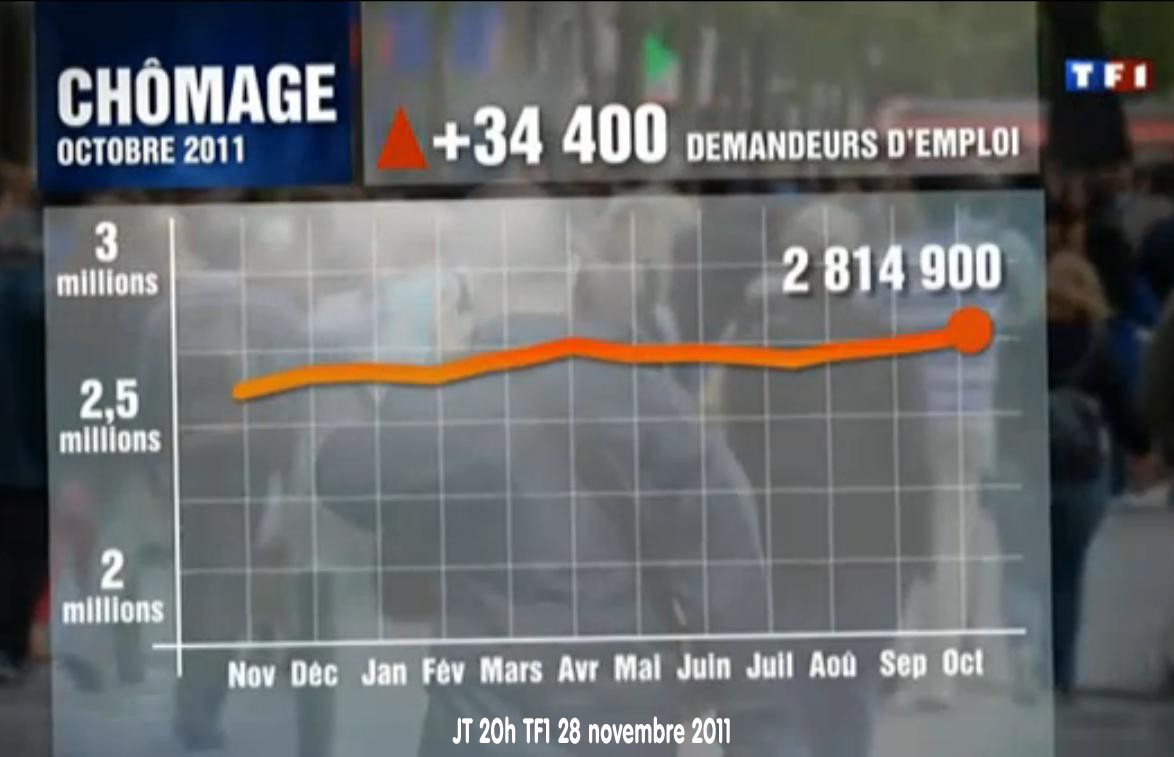

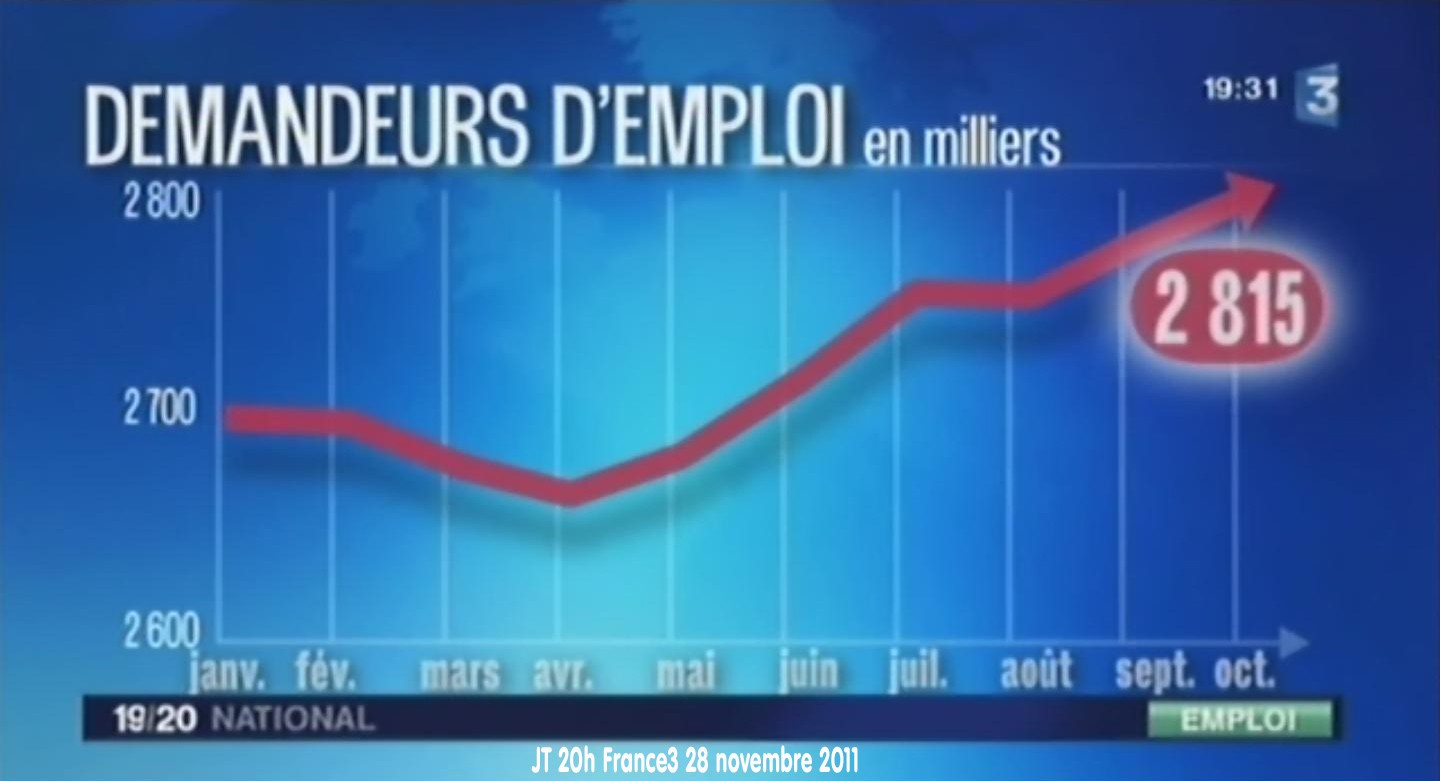
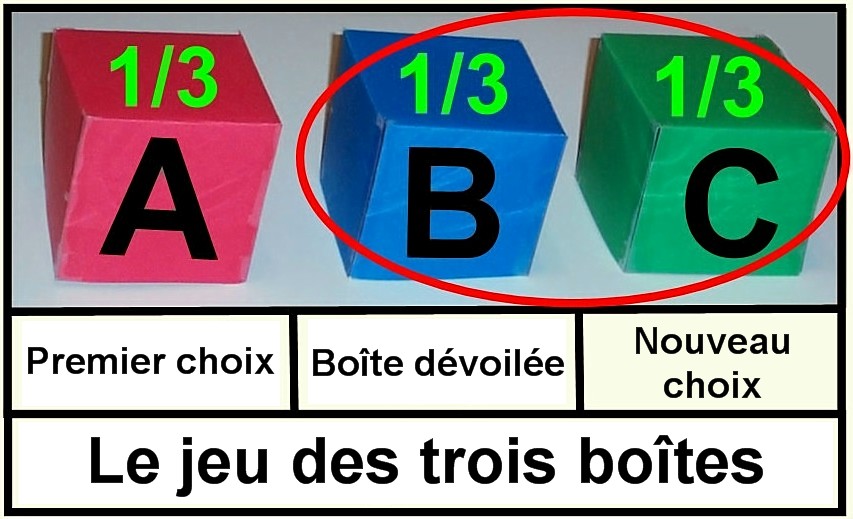 ne changez pas de probabilité de succès, qui demeure un tiers. En changeant toujours de choix, vos chances de succès sont deux fois plus grandes. Car, en dévoilant l’une des boîtes qui n’a pas d’argent sous elle, le maître de cérémonie vous offre effectivement l’ensemble des deux choix qui restent, dont la probabilité égale deux tiers. La figure ci-contre illustre ce concept.
ne changez pas de probabilité de succès, qui demeure un tiers. En changeant toujours de choix, vos chances de succès sont deux fois plus grandes. Car, en dévoilant l’une des boîtes qui n’a pas d’argent sous elle, le maître de cérémonie vous offre effectivement l’ensemble des deux choix qui restent, dont la probabilité égale deux tiers. La figure ci-contre illustre ce concept.

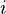 , on a :
, on a :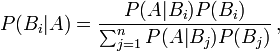

 Puis c’est le regretté Martin Gardner, incontournable pionnier de la pensée critique décédé en 2010, qui l’exhuma en 1959 dans sa rubrique Mathematical Games du Scientific American sous le nom de « problème des trois prisonniers » (« Mathematical Games » column, Scientific American, October 1959, pp. 180–182). Enfin, c’est Steve Selvin qui rouvrit la question dans «
Puis c’est le regretté Martin Gardner, incontournable pionnier de la pensée critique décédé en 2010, qui l’exhuma en 1959 dans sa rubrique Mathematical Games du Scientific American sous le nom de « problème des trois prisonniers » (« Mathematical Games » column, Scientific American, October 1959, pp. 180–182). Enfin, c’est Steve Selvin qui rouvrit la question dans «  Louis Dubé nous offre en prime un court programme commenté en langage Basic qui simule ce problème avec « N » boîtes (donc aussi avec 3 boîtes).
Louis Dubé nous offre en prime un court programme commenté en langage Basic qui simule ce problème avec « N » boîtes (donc aussi avec 3 boîtes).





