
Céline Montet est professeure documentaliste au collège Achille Mauzan, à Gap (Hautes-Alpes). Investie depuis plusieurs années dans l’enseignement de l’esprit critique auprès de ses élèves, elle partage avec nous une séance destinée aux élèves de 4ème de son établissement : comment repérer et identifier quelques arguments fallacieux et autres sophismes. En partant de ce qui existait à destination d’adultes et étudiants (voir ici), elle a conçu cette séance en l’adaptant au niveau des élèves. Bravo pour ce travail orignal et qui, nous l’espérons, sera partagé et repris par d’autres collègues et pour d’autres niveaux !
Objectifs de la séance
Cette séquence s’inscrit dans un projet plus global de développement de l’esprit critique, dans lequel les élèves de 4ème vont aborder les notions de hoax, théories du complot, apprendre à utiliser des outils destinés à vérifier la source d’une image, travailler autour de cas concrets de manipulation par les chiffres et les graphiques, réfléchir autour de l’impact de l’utilisation de termes « chimique » et « naturel » ainsi que de leur validité scientifique, et assister à une intervention de Denis Caroti.
Compétences mises en jeu
Compétences du socle Domaine 1.1 : Langue française à l’oral et à l’écrit Domaine 2 : Les méthodes et outils pour apprendre Domaine 3 : la formation de la personne et du citoyen Domaine 5 : les représentations du monde et l’activité humaine
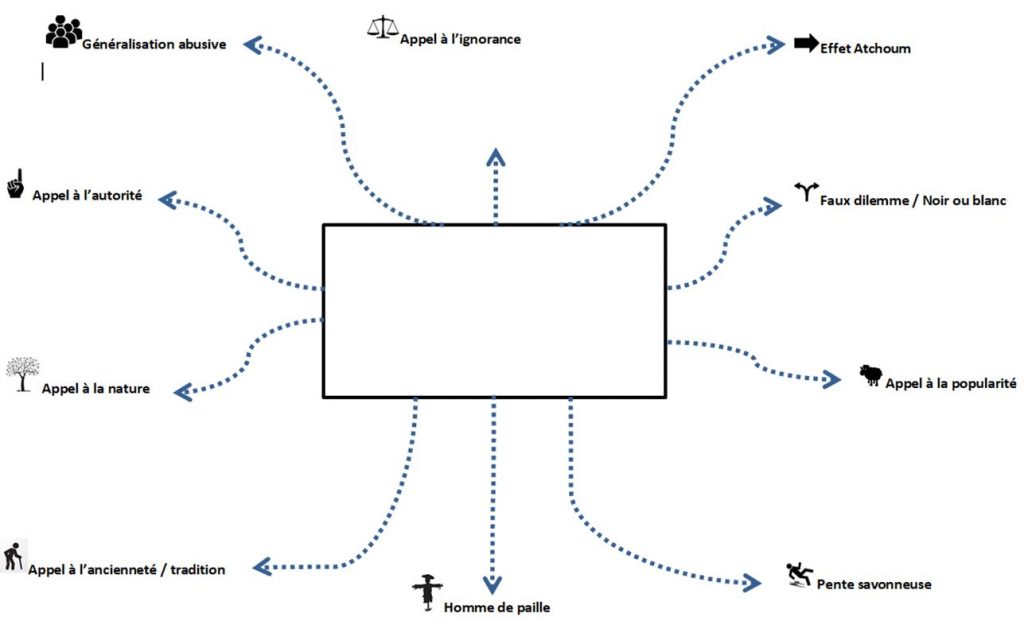
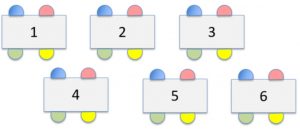
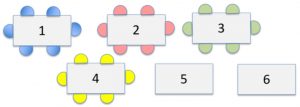
Compétences liées à l'éducation aux médias et à l'information (matrice Traam de l'académie de Toulouse) Être auteur : consulter, s’approprier, publier Argumenter : analyser, développer un point de vue Compétences liées à l'éducation morale et civique Être auteur : consulter, s’approprier, publier Culture du jugement : Culture de l’engagement : L’objectif principal de cette séquence est pour les élèves d’être capable d’identifier 10 arguments fallacieux donnés pour pouvoir ensuite les repérer dans les discours ou les publicités, mais aussi pour éviter d’en formuler soi-même. Nous allons tenter d’atteindre ces objectifs en mettant en place un dispositif pédagogique d’apprentissage collaboratif, appelé « Atelier Jigsaw ». Il s’agit de découper le contenu à s’approprier en plusieurs parties. Dans le cas précis, le contenu est divisé en 5 : deux arguments fallacieux par fiche, soit 10 arguments à connaître en fin de séquence. Dans un premier temps, il s’agira de définir l’expression « Esprit critique », puis d’expliquer aux élèves ce qu’est un argument et quel est son objectif (raisonnement qui a pour but d’appuyer une idée ou au contraire de la réfuter). Pour cela, l’affirmation suivante est notée au tableau : boire du lait de vache est dangereux pour la santé. Je demande aux élèves de se positionner par rapport à cette idée et pourquoi ils adoptent cette position. « Comment vous y prenez-vous pour justifier ou réfuter cette idée ? ». Cela permet de faire ressortir la notion d’argument et donc de la définir. Cependant, il arrive que l’on se retrouve confronté à des arguments invalides. Cette utilisation peut être involontaire ou volontaire : dans ce dernier cas, l’objectif est alors de tromper son auditoire. L’objet de cette séance sera donc de découvrir 10 arguments invalides dits fallacieux : dans ces 10 cas, la forme de raisonnement utilisée ne suffit pas à justifier l’opinion défendue. Méthode d’apprentissage coopératif inventée par Elliot Aronson, psychologue social dont l’objectif premier était de réduire les tensions et préjugés entre différents groupes ethniques. Les élèves sont rassemblés par îlots/groupes Jigsaw (voir ci-dessous), chaque élève autour d’une même table possédant une partie du cours (une couleur différente par fiche). Les élèves sont réunis par groupe d’expertise : ils sont amenés à discuter, échanger, prendre des notes, inventer de nouveaux exemples, dans l’objectif de maîtriser le contenu de leur fiche. Il est précisé aux élèves qu’à l’issue de cette étape, ils devront être experts de leur fiche et être capable d’expliquer son contenu à ceux qui n’ont pas eu cette fiche entre les mains. On reforme les groupes Jigsaw de départ, l’objectif étant maintenant pour chacun de ces groupes de maîtriser collectivement le contenu de chacune des fiches : à charge pour chaque expert de former le reste du groupe. Chaque groupe Jigsaw va ensuite réaliser une tâche collective. Groupe 1 : défendre un projet de loi en avançant le plus d’arguments fallacieux possibles. Exemples : il faut interdire les enfants dans les supermarchés / Seules les personnes âgées de moins de 50 ans ont le droit d’acquérir un caniche . La restitution du travail se fait sur la fiche ci-dessous (carte mentale au format A3) Groupe 2 : imaginer des slogans pour un produit en utilisant le plus d’arguments fallacieux possibles. Exemples : slogans pour la lessive « Céclin’ » / la boisson énergétique « Géla’pêche » (variante légume : « Géla’patate »).La restitution du travail se fait sur la fiche ci-dessous (carte mentale au format A3) Groupe 3 : justifier une idée/opinion à l’aide d’arguments fallacieux. Exemples : les personnes dont le prénom commence par la lettre C sont plus intelligentes que les autres / Manger des glaces contribue au réchauffement climatique / Écouter de la musique classique provoque des pertes de mémoire. La restitution du travail se fait sur la fiche ci-dessous (carte mentale au format A3) Groupe 4 : Identifier le type d’argument fallacieux utilisé dans chacun des exemples distribués (un seul type d’argument par document). La restitution du travail se fait sur des affiches, en rassemblant les exemples selon les types d’arguments relevés. Groupe 5 : Repérer et identifier les arguments fallacieux utilisés pour chacun des exemples distribués (plusieurs types d’arguments par document). Les élèves doivent surligner ou souligner les arguments repérés et les nommer en marge. Les connaissances des élèves ont été évaluées à l’aide d’un questionnaire à compléter individuellement à l’issue de ce travail, en vue de vérifier si les connaissances avaient été acquises et donc si la méthode utilisée s’était révélée efficace. De manière générale : J’aurais plutôt dû constituer des groupes pairs, car à 5, un élève se trouve géographiquement un peu en retrait (et ainsi sélectionner 8 arguments au lieu de 10). Avant la constitution des groupes d’experts : Demander à un élève de reformuler la consigne avant de constituer les groupes experts, pour être sûr qu’elle soit comprise et éviter de perdre du temps à devoir la reformuler au sein de chaque groupe. Leur demander de sortir un brouillon pour qu’ils aient de quoi prendre des notes.Présentation de la séquence
Introduction de la séquence
Atelier Jigsaw : une méthode pédagogique en 3 étapes (Aronson, 1971)
Première étape : découverte silencieuse du contenu de la fiche

Deuxième étape : discussion entre experts

Troisième étape : partage des connaissances

Réalisation d’une tâche collective
TéléchargerÉvaluation
Remarques – bilan












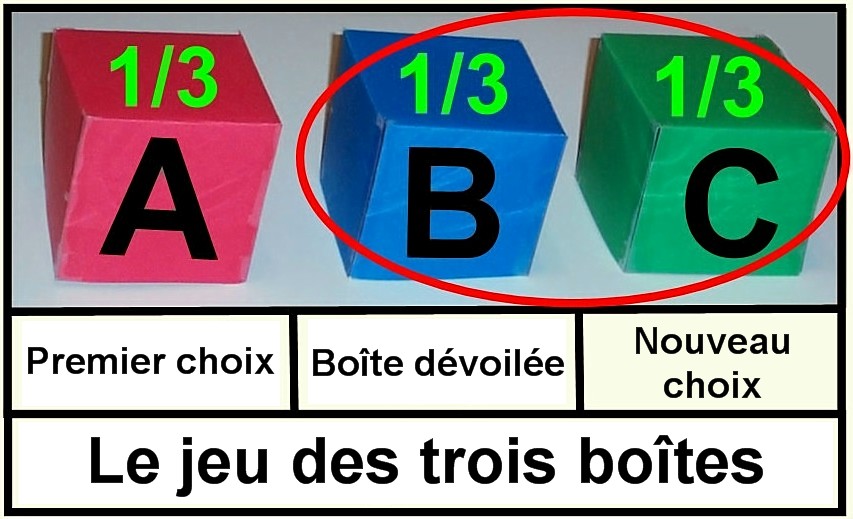 ne changez pas de probabilité de succès, qui demeure un tiers. En changeant toujours de choix, vos chances de succès sont deux fois plus grandes. Car, en dévoilant l’une des boîtes qui n’a pas d’argent sous elle, le maître de cérémonie vous offre effectivement l’ensemble des deux choix qui restent, dont la probabilité égale deux tiers. La figure ci-contre illustre ce concept.
ne changez pas de probabilité de succès, qui demeure un tiers. En changeant toujours de choix, vos chances de succès sont deux fois plus grandes. Car, en dévoilant l’une des boîtes qui n’a pas d’argent sous elle, le maître de cérémonie vous offre effectivement l’ensemble des deux choix qui restent, dont la probabilité égale deux tiers. La figure ci-contre illustre ce concept.

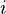 , on a :
, on a :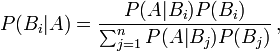

 Puis c’est le regretté Martin Gardner, incontournable pionnier de la pensée critique décédé en 2010, qui l’exhuma en 1959 dans sa rubrique Mathematical Games du Scientific American sous le nom de « problème des trois prisonniers » (« Mathematical Games » column, Scientific American, October 1959, pp. 180–182). Enfin, c’est Steve Selvin qui rouvrit la question dans «
Puis c’est le regretté Martin Gardner, incontournable pionnier de la pensée critique décédé en 2010, qui l’exhuma en 1959 dans sa rubrique Mathematical Games du Scientific American sous le nom de « problème des trois prisonniers » (« Mathematical Games » column, Scientific American, October 1959, pp. 180–182). Enfin, c’est Steve Selvin qui rouvrit la question dans «  Louis Dubé nous offre en prime un court programme commenté en langage Basic qui simule ce problème avec « N » boîtes (donc aussi avec 3 boîtes).
Louis Dubé nous offre en prime un court programme commenté en langage Basic qui simule ce problème avec « N » boîtes (donc aussi avec 3 boîtes).

