Vous connaissiez les formidables cours de Zététique et autodéfense intellectuelle de l’inénarrable Richard Monvoisin ? Depuis 2019, ce sont nos collègues Jérémy Attard et Denis Caroti qui se sont lancés dans l’aventure. S’adressant à tous les étudiants en première année de licence de Psychologie de l’Université de Nîmes, ce cours est en quelque sorte le petit frère de celui de Grenoble. En voici quelques détails.
Lorsque Jonathan Delmonte, chercheur en psychologie clinique et psychopathologie, nous a demandé si nous voulions bien dupliquer les enseignements de Richard dans son université, la réponse fut rapide : oui, bien entendu ! Dès janvier 2019, un nouveau cours est donc né : 12x2h pour presque 400 étudiants de l’université de Nîmes (L1 psychologie) et un sacré boulot pour corriger les dossiers sur lesquels ils planchent pendant plusieurs semaines… mais finalement, la satisfaction de transmettre des connaissances, des outils pratiques et méthodologiques et surtout un état d’esprit : rationalité, souci de la preuve, humilité intellectuelle, curiosité et envie d’aller toujours (se) questionner.
Le programme des cours (qui varie à la marge) :
- Introduction à la zététique, l’esprit critique et l’autodéfense intellectuelle
- Qu’est-ce qu’une ‘bonne’ preuve ? Fiabilité de nos perceptions, biais cognitifs et témoignages
- Quelques bases d’épistémologie pratique (1)
- Quelques bases d’épistémologie pratique (2)
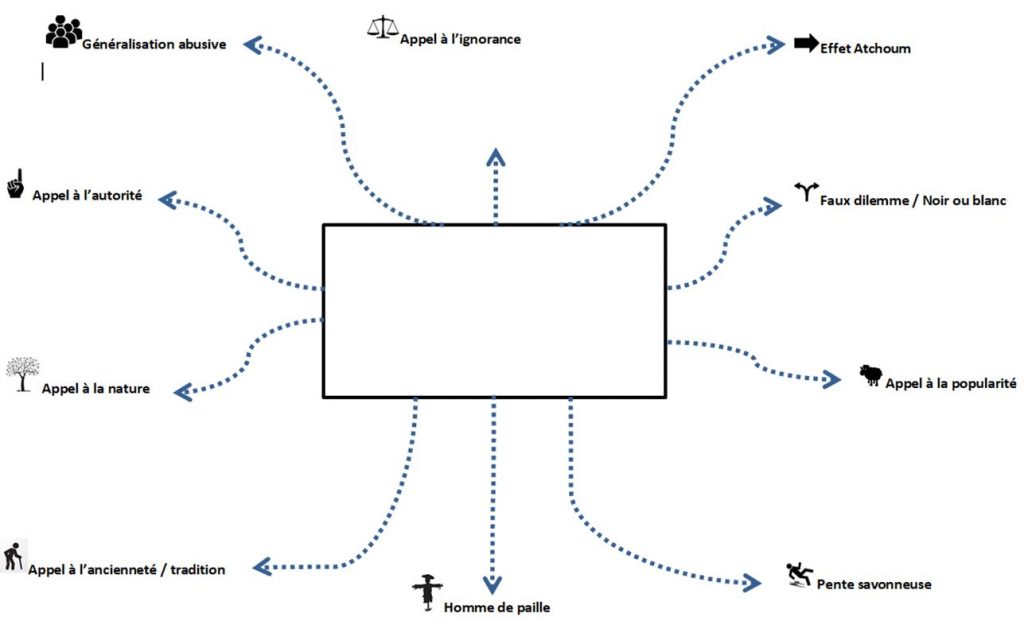
- Arguments fallacieux et raisonnements
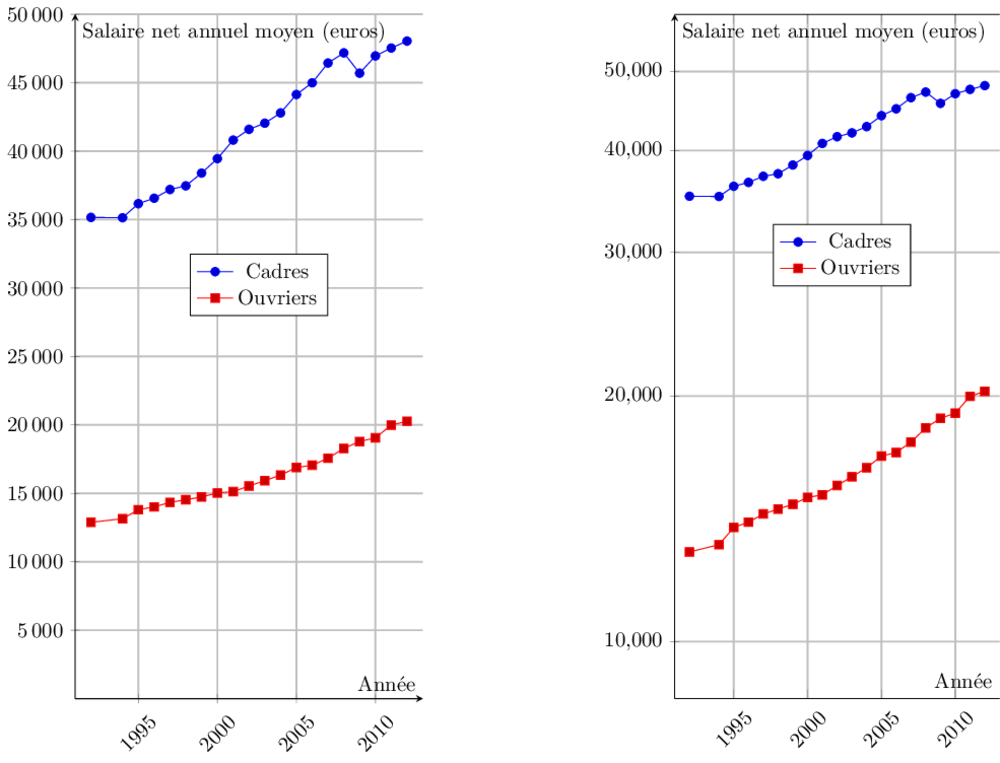
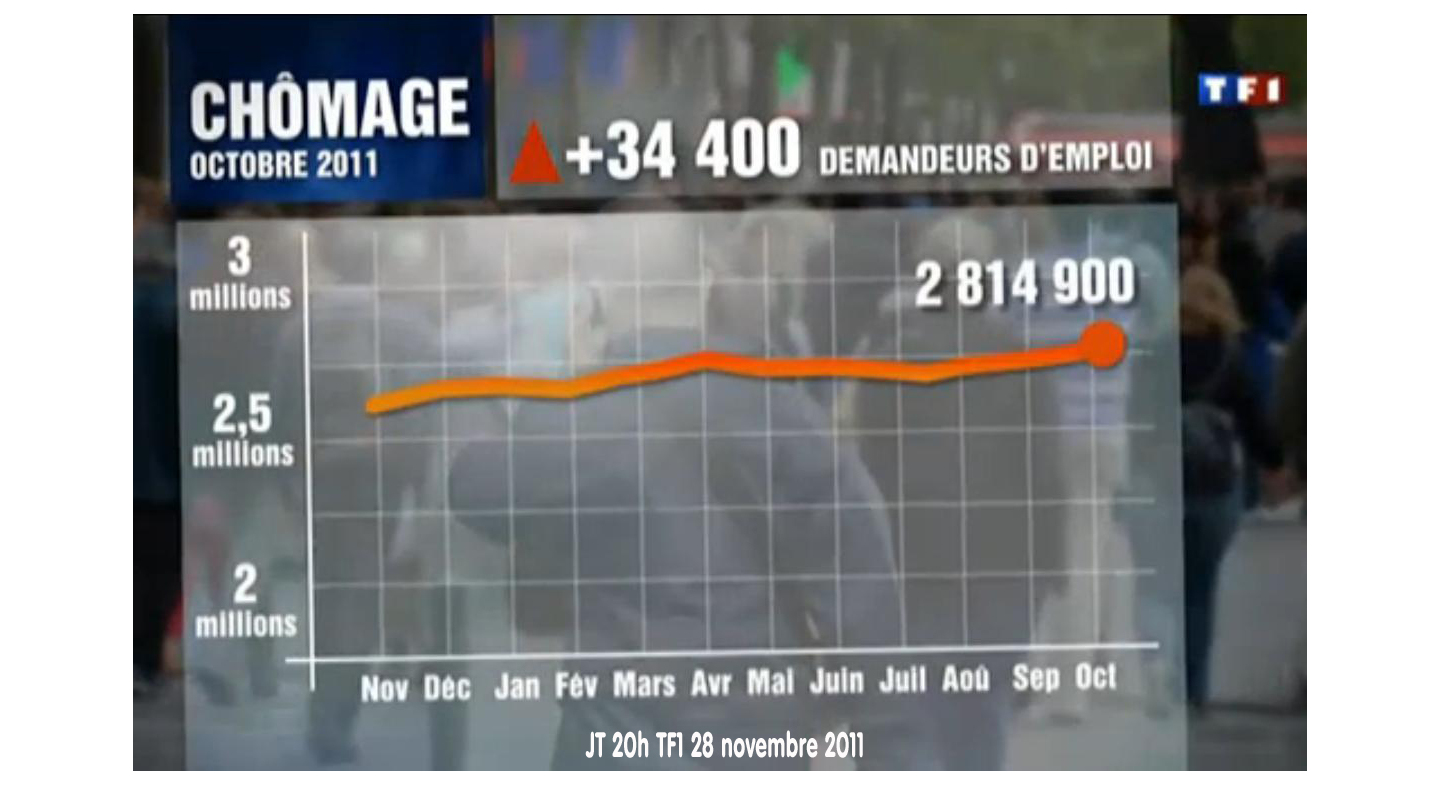
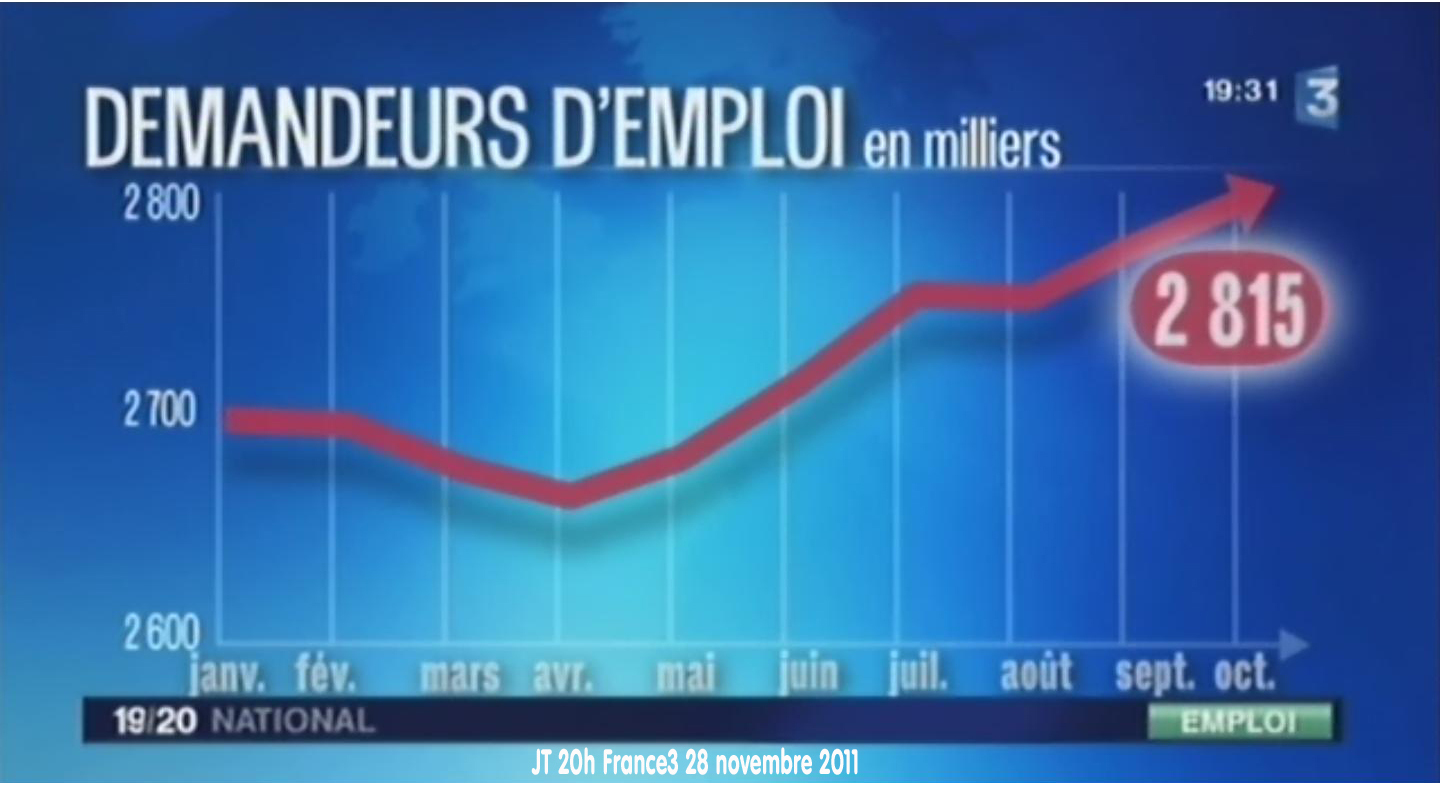
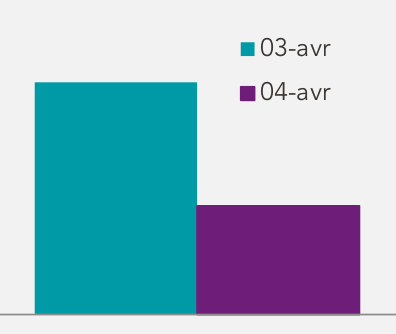
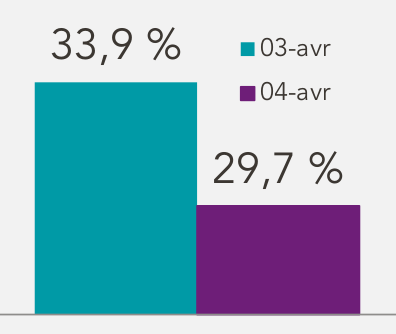
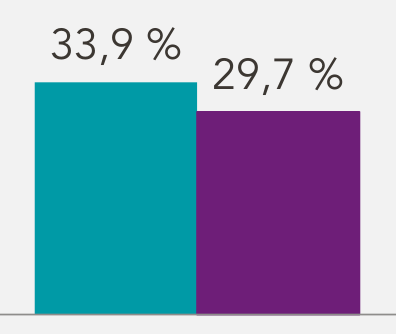
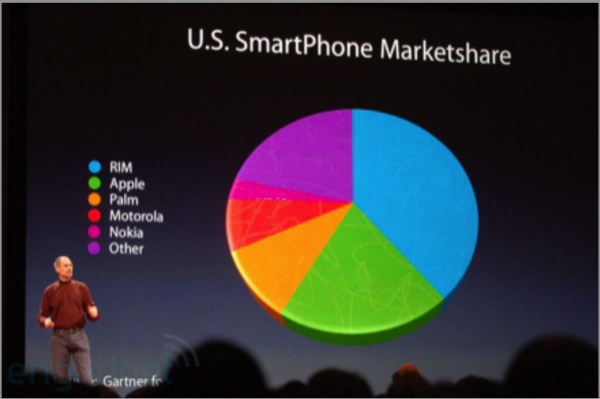
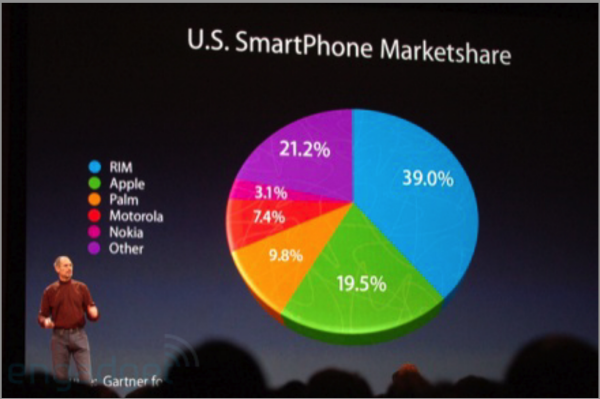
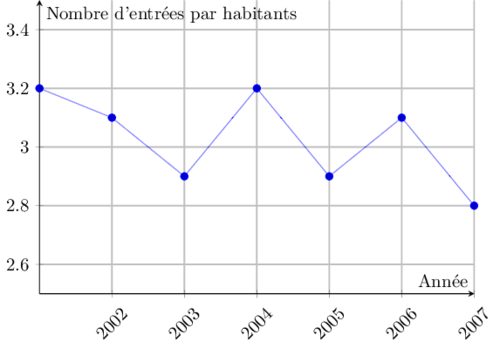
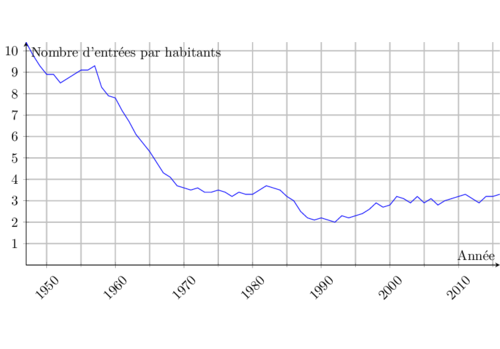
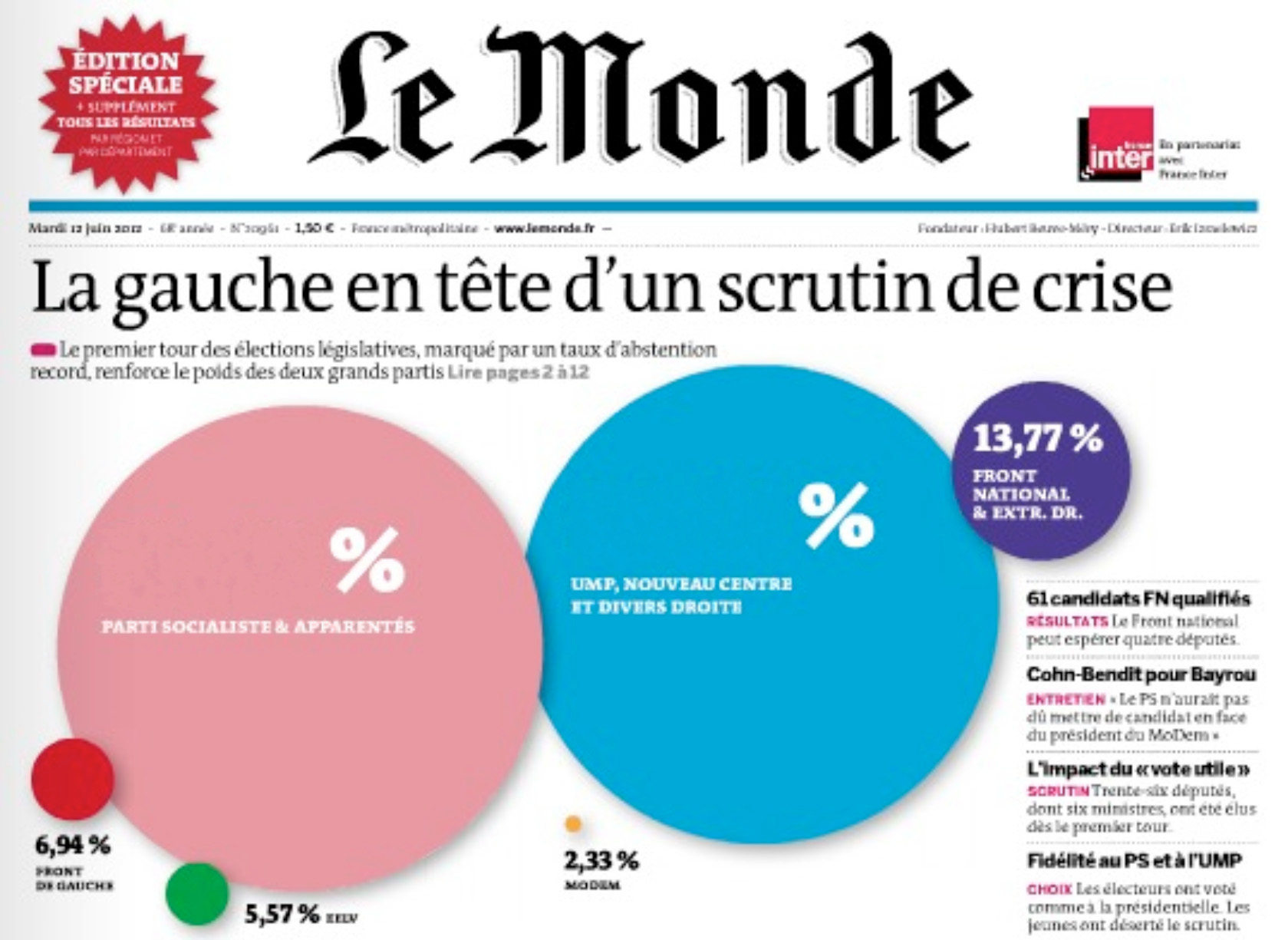
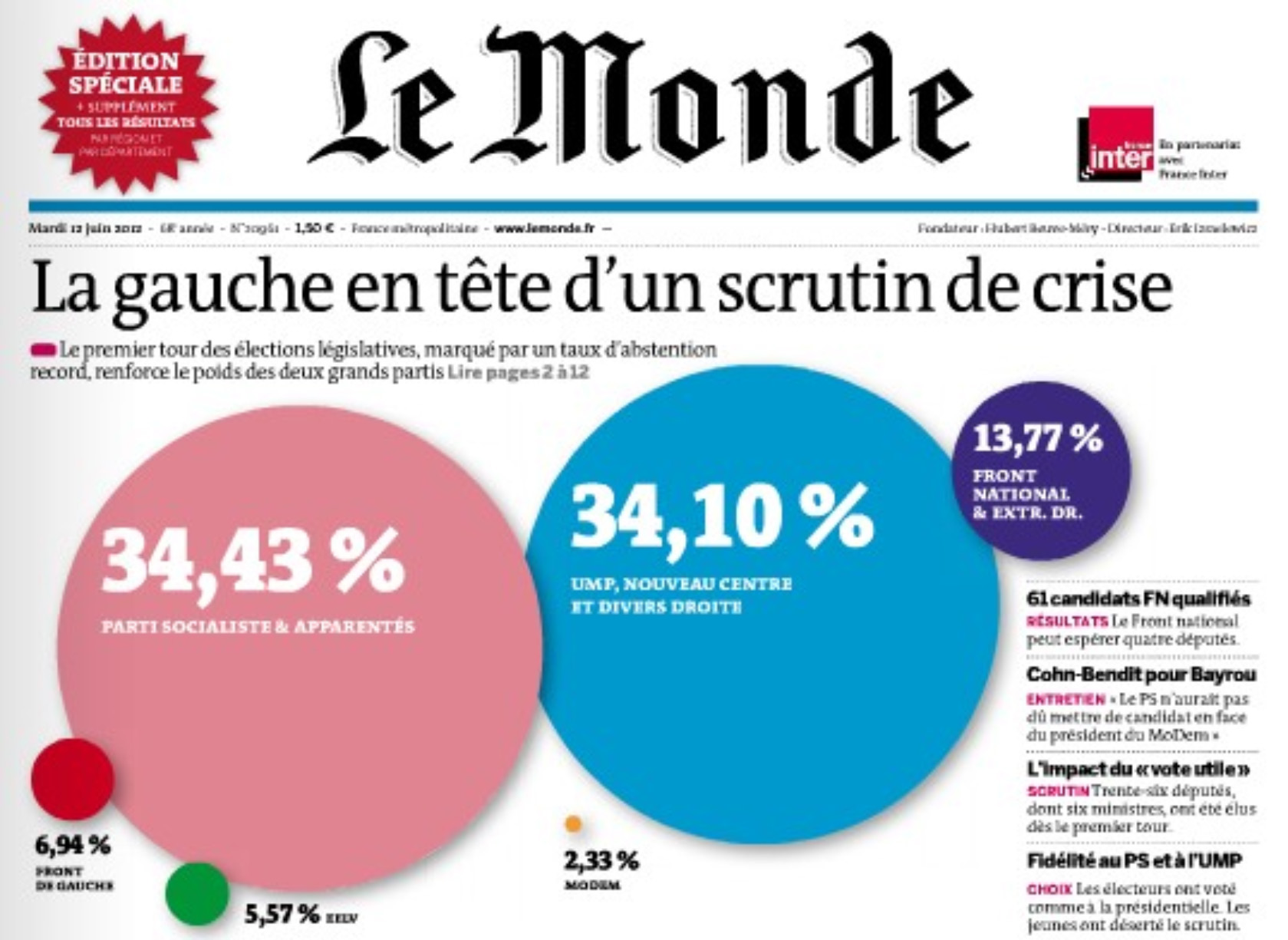
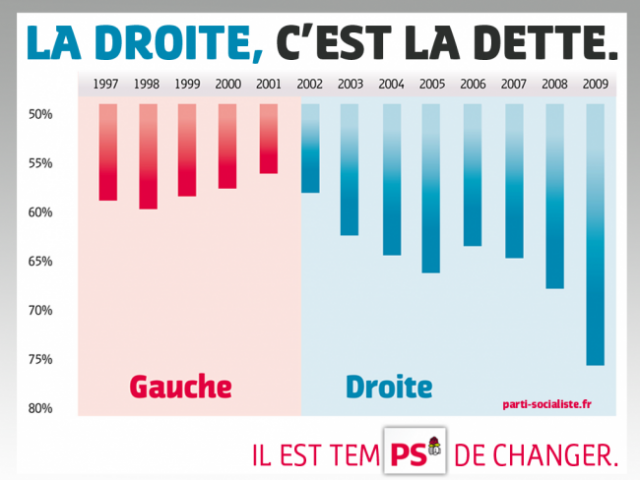
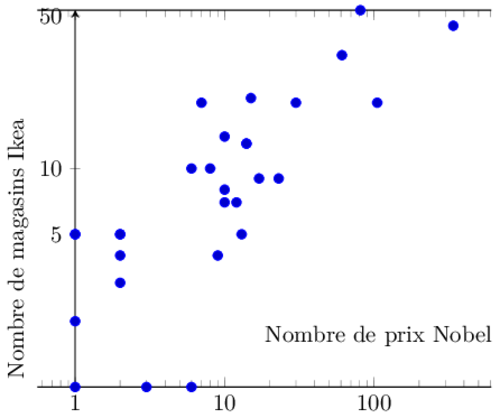
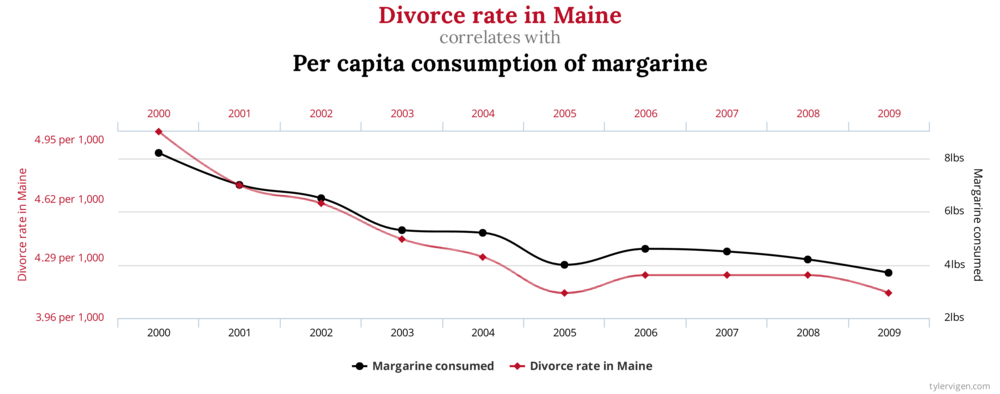
- Chiffres, statistiques et graphiques
- Langage et effets : Barnum, paillasson, impact
- Hasard, coïncidences et scénarios complotistes
- La Nature et ses dérives
- Médecines alternatives : le cas de l’homéopathie
- Les créationnismes
- Prison, justice et philosophie morale
Les contenus sont accessibles sur simple demande par mail : contact-at-cortecs.org
L’ouverture d’un tel cours est suffisamment rare en France pour remercier Jonathan Delmonte et toute l’équipe enseignante pour leur confiance et envie de faire naître ce cours. Et bien entendu un merci spécial à Richard Monvoisin qui a plus qu’inspiré le contenu distillé aux étudiants mais également à Henri Broch, qui lança les premiers enseignements de zététique il y a plus de 30 ans à Nice.